A KöMaL 2007. januári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2007. február 15-én LEJÁRT. |
K. 109. A labdarúgó bajnokság negyedik fordulója után Péter kedvenc csapata három gólt rúgott és két gólt kapott. Tudjuk, hogy győzelemért 3 pont, döntetlenért 1 pont jár, a vesztes csapat nem kap pontot. Hány pontja lehet Péter kedvenc csapatának a negyedik forduló után?
(6 pont)
K. 110. A Sárkányvárban a 14 fejű sárkánygyerek alszik, miközben sárkánymamája palacsintát süt, és egy tálra teszi, majd elmegy otthonról. Felébred az egyik fej, megeszi a palacsinták 1/11-ed részét, majd elalszik. Ezután felébred egy másik fej is, ő megeszi a tálon található palacsinták 1/13-ad részét, és újra elalszik. Ezt követően 3 fej ébred együtt, akik fejenként a tálon található palacsinták 1/14--1/14 részét eszik meg, majd felkeltik a többi fejet is. Akik ettek, azok már nem kapnak a palacsintából, így a 9 éhes fej egymás között szétosztja a maradékot (nem feltétlenül egyenlően). Mindig minden fej egész számú palacsintát evett. Mennyi palacsinta lehetett eredetileg a tálon, ha az egész tál palacsinta igazságos szétosztásával senki sem kapott volna 143-nál többet?
(6 pont)
K. 111. Egy játékban két kockával dobunk. Van 9 darab számkártyánk 1--9-ig számozva, az ezeken szereplő számok összegeként (vagy csak egy kártyát felhasználva) kell a kockákkal dobott számok összegét kirakni, de egy számkártyát csak egyszer használhatunk fel. Ezután újra dobunk, és a maradék számkártyákból ismét megpróbáljuk kirakni a dobott összeget, és így tovább, amíg ez már nem lehetséges.
a) Legkevesebb hány dobásból állhat egy olyan sorozat, amikor az összes számkártyát fel tudjuk használni? Mutassunk is rá példát.
b) Legrosszabb esetben legkevesebb hány dobás után áll meg a játék?
(6 pont)
K. 112. A következő helyes összeadás minden sorából töröltünk egy-egy számjegyet, a megmaradt számokat összetoltuk egy-egy háromjegyű számmá és az összeadás helyes maradt. Ezután ugyanígy képeztünk kétjegyű számokat, majd egyjegyűeket és az összeadás mindkét lépésben helyes maradt. Melyek lehettek az egyes lépésekben eltávolított számok? Adjuk meg az összes lehetőséget.
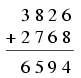
(6 pont)
K. 113. Hány olyan 5-re végződő, különböző számjegyekből álló négyjegyű szám van, amely minden számjegyével osztható?
(6 pont)
K. 114. Pisti osztálytársai között három Kovács, négy Nagy, egy Kis és két Takács van. A fiúk keresztnevei között négy Laci, két Sanyi, három Robi és egy Marci található (minden fiúnak csak egy keresztneve van, és nincs két teljesen azonos nevű gyerek az osztályban). Mi a teljes neve Pisti ezen osztálytársainak?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2007. február 15-én LEJÁRT. |
C. 880. Egy hatjegyű számot úgy lehet hárommal szorozni, hogy az első jegyét hárommal csökkentjük és a végére írunk egy hármast. Melyik ez a szám?
(5 pont)
C. 881. Oldjuk meg az egyenletet.
(5 pont)
C. 882. Egy derékszögű háromszög befogóinak hossza a és b. A derékszög csúcsát az átfogó egy pontjával összekötő d hosszúságú szakasz az a befogóval  szöget zár be. Igazoljuk, hogy
szöget zár be. Igazoljuk, hogy
(5 pont)
C. 883. Egy vályú, amelynek keresztmetszete szabályos háromszög, színültig van vízzel. A víz egyötödét ki akarjuk belőle önteni. Hány fokkal kell ehhez a vályút megdönteni úgy, hogy a végeit határoló háromszögek a saját, függőleges síkjukban mozogjanak?
(5 pont)
C. 884. Egy kockadobást nevezzünk sikeresnek, ha a dobott szám legalább három. Mi a valószínűbb: az, hogy két dobásból legalább egy sikeres, vagy az, hogy négy dobásból legalább kettő?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2007. február 15-én LEJÁRT. |
B. 3962. 1000 Ft-ot kell kifizetnünk, de csak 100, 20 és 5 Ft-os érméink vannak. Hányféleképpen lehetséges ez, ha ehhez pontosan 100 db érmét használunk fel? (Az érmék kifizetésének sorrendjére nem vagyunk tekintettel.)
(3 pont)
B. 3963. Egy bábut kell eljuttatnunk a sakktábla bal alsó sarkából az átellenes sarokba úgy, hogy egyesével léphetünk jobbra vagy felfelé. Hány olyan útvonal van, amelyik áthalad a középső négy mező valamelyikén?
(4 pont)
B. 3964. Az ABC derékszögű háromszög befogóinak hossza AC=3 és BC=4. Az A pontot elmozdítottuk BC-vel párhuzamosan az A1 pontba, ezután a B pontot elmozdítottuk az A1C egyenessel párhuzamosan a B1 pontba, végül C-t mozdítottuk el A1B1-gyel párhuzamosan a C1 pontba úgy, hogy a kapott A1B1C1 háromszög B1-ben derékszögű, az A1B1 befogójának hossza pedig 1 egység. Milyen hosszú lett a B1C1 befogó?
(3 pont)
B. 3965. Az ABC hegyesszögű háromszög AB és AC oldala fölé kifelé félköröket rajzolunk. A szemközti csúcsokból húzott magasságvonalak egyenesének a félkörökkel való metszéspontja legyen M és N. Bizonyítsuk be, hogy AM=AN.
(3 pont)
B. 3966. Egy iskolai sakkversenyen mindenki mindenkivel pontosan egyszer játszott. Minden játékos ugyanannyi pontot szerzett a lányok ellen, mint a fiúk ellen. Bizonyítsuk be, hogy a résztvevők száma négyzetszám. (Győzelemért 1; döntetlenért 0,5; vereségért 0 pont jár.)
(5 pont)
B. 3967. Szerkesszük meg a háromszöget, ha adott egy szöge, továbbá a szög csúcsából induló magasságának és súlyvonalának hossza.
(4 pont)
B. 3968. Oldjuk meg az alábbi egyenlőtlenséget:
(4 pont)
B. 3969. Mi egy hegyesszögű háromszög köré írt szabályos háromszögek középpontjainak halmaza? (A G háromszög a H köré van írva, ha H csúcsai a G oldalaira illeszkednek.)
(5 pont)
B. 3970. Bizonyítsuk be, hogy egy egységnyi oldalú szabályos hétszög átlói hosszának harmonikus közepe 2.
(4 pont)
B. 3971. A nemnegatív x, y, z számok összege 1. Legyen
Milyen nagy lehet S, illetve C?
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2007. február 15-én LEJÁRT. |
A. 416. Az ABC derékszögű háromszög C-ből induló magasságának talppontja az AB átfogón F. Az AC befogó egy tetszőleges P pontjának vetülete az átfogón Q. A B-ben BP-re állított merőleges és a CF egyenes metszéspontja legyen R. Bizonyítsuk be, hogy az AC és FQ átmérőjű körök F-től különböző metszéspontja a PR szakasz belsejébe esik.
(5 pont)
A. 417. n 3 ember egymás után többször fut versenyt egymással (holtverseny sohasem alakul ki). Jelölje f(n) a legkisebb olyan egész számot, ahány verseny után előfordulhat, hogy az n ember közül bárhogyan választunk ki hármat, közöttük mind a hatféle sorrend előfordul. Igazoljuk, hogy
3 ember egymás után többször fut versenyt egymással (holtverseny sohasem alakul ki). Jelölje f(n) a legkisebb olyan egész számot, ahány verseny után előfordulhat, hogy az n ember közül bárhogyan választunk ki hármat, közöttük mind a hatféle sorrend előfordul. Igazoljuk, hogy
ln n<f(n)<20ln n.
Javasolta: Pach Péter Pál és Puskás Anna, Budapest
(5 pont)
A. 418. Mutassuk meg, hogy tetszőleges 0<a<b valós számpárhoz létezik olyan n pozitív egész, amire
( (m) jelöli az m-nél nem nagyobb, m-mel relatív prím pozitív egészek számát.)
(m) jelöli az m-nél nem nagyobb, m-mel relatív prím pozitív egészek számát.)
Olasz feladat
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

