A KöMaL 2007. márciusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2007. április 11-én LEJÁRT. |
M. 277. Méréssel ellenőrizzük, hogy mikor lesz hidegebb a keletkező tejeskávé: ha rögtön beleöntjük a forró kávéba a hideg tejet, majd bizonyos ideig állni hagyjuk szobahőmérsékleten, vagy ha először állni hagyjuk a forró kávét (az előbbivel azonos ideig), és csak azután öntjük bele a hideg tejet!
Közli: Fried Ervin, Budapest
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2007. április 11-én LEJÁRT. |
P. 3963. Mekkora tömegű testet kellene felemelni 1 méter magasra ahhoz, hogy ugyanakkora legyen az energiaváltozás, mint amikor 1 liter vizet -kal melegítünk fel?
Hatvani István fizikaverseny, Debrecen
(3 pont)
P. 3964. Honnan kap vízszintes lendületet az a gyerek, aki a hintán ,,belengeti'' magát? (Kezdetben mozdulatlanul ül a hintán, és a lába nem ér le a földre.)
Közli: Vass Miklós, Budapest
(4 pont)
P. 3965. R sugarú, rögzített, érdes félgömb tetejéről kezdősebesség nélkül legördül egy r sugarú, m tömegű golyó. Hol csúszik meg és mekkora a megcsúszás pillanatában a súrlódási erő, ha R=1 m, r=0,1 m, m=15 kg, a tapadó súrlódás együtthatója 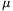 =
=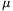 0=0,2?
0=0,2?
Közli: Holics László, Budapest
(5 pont)
P. 3966. Két pontszerű hullámforrásból, melyek 5 Hz frekvenciával azonos fázisban rezegnek, azonos amplitúdójú hullámok indulnak ki. A hullámok terjedési sebessége 2 m/s. Mit tapasztalunk a hullámtér azon pontjában, amely az egyik hullámforrástól 40 cm, a másiktól 60 cm távolságra van?
Nagy László fizikaverseny, Kazincbarcika
(4 pont)
P. 3967. Egy tartályban hélium- és hidrogéngáz keveréke található. A két gáz tömegének milyen aránya esetén lesz a két gáz parciális nyomása egyenlő?
Tarján Imre fizikaverseny, Szolnok
(4 pont)
P. 3968. Este nyolckor zártuk el a kerti vízcsapot, de sajnos rosszul. Lefelé vékonyodó sugárban folyik belőle a víz, az ábrán látható módon. A vízsugár kör keresztmetszetű, átmérője az egyik helyen 6 mm, ennél 4 cm-rel lejjebb már csak 3,4 mm. Mennyi vizet pazarolunk el, ha csak másnap reggel nyolckor zárjuk el rendesen a csapot? (Az áramló víz belső súrlódását elhanyagolhatjuk.)
Közli: Légrádi Imre, Sopron
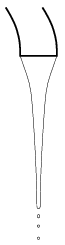
(5 pont)
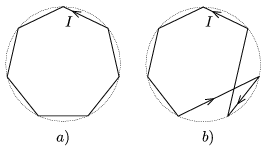
P. 3969. Szigetelő huzalból készült két hurok mindegyikében azonos I erősségű áram folyik az ábrán jelölt irányban. A hurkok csúcspontjai egy szabályos n-szöget alkotnak. Melyik esetben lesz nagyobb a mágneses tér a hurkok köré írt kör középpontjában?
Közli: Cserti József, Budapest
(5 pont)
P. 3970. A B=10-3 T mágneses indukciójú, d=2 cm szélességű homogén mágneses mezőbe egy elektront lövünk be a mágneses erővonalakra merőlegesen, a határfelületre merőleges egyenessel  =30o-os szöget bezáróan.
=30o-os szöget bezáróan.
a) Legalább mekkora sebességgel kell belőni az elektront ahhoz, hogy áthaladjon a d szélességű homogén mágneses mezőn?
b) Mekkora az a sebesség, amelynél kisebb belövési sebességek esetén semmiképpen nem tudjuk átjuttatni az elektront a d szélességű homogén mágneses mezőn?
Közli: Kotek László, Pécs
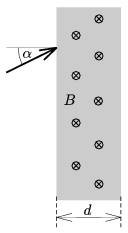
(5 pont)
P. 3971. 1611-ben, a Snellius-Descartes féle törvény felfedezése előtt megjelent Dioptrice című könyvében Kepler a levegőből hegyikristályba lépő fénysugár törését tanulmányozva azt találta, hogy a beeső sugár meghosszabbítása és a megtört sugár közti 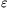 szög arányos a beesés
szög arányos a beesés  szögével:
szögével: , ahol k egy állandó. (A hegyikristály esetén
.)
a) Igazoljuk Kepler képletének helyességét kis beesési szögekre!
b) Bocsássunk egy monokromatikus fénysugarat kicsiny  törőszögű hegyikristály prizmára, közelítőleg merőlegesen! Határozzuk meg a beeső és a kilépő sugár közötti
törőszögű hegyikristály prizmára, közelítőleg merőlegesen! Határozzuk meg a beeső és a kilépő sugár közötti  szöget Kepler formulája alapján!
szöget Kepler formulája alapján!
Közli: Horváthy Péter, Tours (Franciaország)
(5 pont)
P. 3972. Hány százalékkal változik meg a folytonos röntgenspektrum legrövidebb hullámhossza, ha a röntgencső feszültségét 10%-kal növeljük?
Közli: Radnai Gyula, Budapest
(4 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

