A KöMaL 2007. októberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2007. november 10-én LEJÁRT. |
K. 133. Hány olyan ötjegyű szám van, melyben a számjegyek összege megegyezik a számjegyek négyzetének összegével?
(6 pont)
K. 134. Egy pozitív egész számról tudjuk, hogy osztható 2-vel, 5-tel és 9-cel. Tudjuk még azt is, hogy ezeken a számokon kívül pontosan 9 további pozitív osztója van. Melyik ez a pozitív egész szám?
(6 pont)
K. 135. Két pakli 32 lapos magyar kártyát külön-külön megkeverünk, majd az egyik pakli tetejére helyezzük a másik paklit. Ezután minden, a felső pakliban levő lapnak megkeressük a párját az alsó pakliban, és megszámoljuk, hogy közöttük hány kártyalap helyezkedik el. Az így kapott számokat összeadjuk. Mennyi lesz ez az összeg?
(6 pont)
K. 136. Egy iskola a nyári szünetben minden tanulóját egyszer táboroztatta. Ezt két egyforma létszámú csoportban tudta megvalósítani. Az iskola fiútanulóinak 70%-át az első, a lánytanulóinak 80%-át a második csoportba osztották be. Az első táborozásban részt vevő gyerekek hány %-a volt fiú?
(6 pont)
K. 137. Az A halmaz elemszáma több, mint a B halmaz elemszáma, de kevesebb, mint B elemszámának kétszerese. Tudjuk továbbá, hogy a B halmaznak 16-tal több részhalmaza van, mint a C halmaznak. Hány részhalmaza lehet az A halmaznak?
(6 pont)
K. 138. Egy tetszőleges, 3-nál nagyobb prímszám négyzetéből kivonunk 1-et. Melyik az a legnagyobb pozitív egész szám, amely biztosan osztója lesz az eredménynek?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2007. november 15-én LEJÁRT. |
C. 910. Egy kör kerületére kilenc egész számot írunk, amelyek összege 90. Bizonyítsuk be, hogy van négy egymás melletti szám, amelyek összege legalább 40.
(5 pont)
C. 911. Melyek azok az n pozitív egész számok, amelyek esetén n3+1 és n2-1 is osztható 101-gyel?
(5 pont)
C. 912. Van-e olyan derékszögű háromszög, amelyben az oldalak a, b, c hossza egész szám, (a,b,c)=1 és az egyik súlyvonalának hossza 7,5?
(5 pont)
C. 913. Az ABC háromszögbe írható kör középpontja O, a BC oldalhoz írható kör középpontja K. Mikor lesz a BKCO négyszög deltoid? Mikor lesz téglalap?
(5 pont)
C. 914. Egy futballcsapat edzője szerint játékosai 95%-os biztonsággal rúgják be a tizenegyest. Mi a valószínűsége annak, hogy öt játékos közül pontosan három hibázik?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2007. november 15-én LEJÁRT. |
B. 4022. Van-e olyan számrendszer, amelyben a 9-cel való oszthatóság szabálya olyan, mint a tízes számrendszerben a 4-gyel való oszthatósági szabály; a 4-gyel való oszthatóság szabálya olyan, mint a tízes számrendszerben a 9-cel való oszthatósági szabály; a 7-tel való oszthatóság pedig pusztán az utolsó számjegy alapján eldönthető?
(4 pont)
B. 4023. Egy háromszög egyik oldalán adott egy pont. Szerkesszünk ezen át két olyan egyenest, amelyek a háromszög területét harmadolják.
(3 pont)
B. 4024. Az első 1000 pozitív egész szám közül legfeljebb hányat választhatunk ki úgy, hogy semelyik két kiválasztott szám összege ne legyen osztható a különbségükkel?
(3 pont)
B. 4025. Az ABC háromszög BC oldalára kifelé, CA oldalára pedig befelé emelt szabályos háromszög harmadik csúcsa A* és B*. A C pontnak az AB egyenesre való tükörképe C'. Bizonyítsuk be, hogy az A*, B* és C' pontok egy egyenesre illeszkednek.
(4 pont)
B. 4026. A d1 és d2 átmérőjű körök közös húrjának hossza h. Az egyik metszésponton át húzott két egyenes a köröket rendre a C1 és C2, illetve a D1 és D2 pontokban metszi az ábrán látható módon. Bizonyítsuk be, hogy a C1D1 egyenes pontosan akkor merőleges C2D2-re, ha
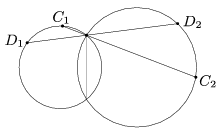
(4 pont)
B. 4027. Oldjuk meg az
egyenletet.
(4 pont)
B. 4028. Két gömb sugara 5 és 3 egység, középpontjaik távolsága 4 egység. Számítsuk ki a két gömb közös részének térfogatát.
(3 pont)
B. 4029. Az r és s pozitív számok összege 1. Mutassuk meg, hogy
rr.ss+rs.sr 1.
1.
Javasolta: R. F. Stöckli (Buenos Aires)
(5 pont)
B. 4030. Adott a síkon az AB szakasz. Vegyünk fel egy tetszőleges C pontot a síkban úgy, hogy az ABC háromszög ne legyen egyenlő szárú. A C csúcshoz tartozó külső szögfelező az AB egyenest D-ben, az ADC körhöz A-ban húzott érintőt P-ben metszi. Határozzuk meg a lehetséges P pontok mértani helyét.
Osztrák versenyfeladat nyomán
(5 pont)
B. 4031. Legyen n>1 egész szám. Bizonyítsuk be, hogy az
egyenletnek nincs racionális megoldása.
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2007. november 15-én LEJÁRT. |
A. 434. Az A, B, C pontok ay MNPQRS konvex hatszög belsejében helyezkednek el úgy, hogy az ABC, NAM, PQB és CRS háromszögek hasonlók. Legyen X, Y és Z az NP, a QR, illetve az SM szakasz felezőpontja, és legyen G, K és I az ABC, ay MPR, illetve az NQS háromszög súlypontja. Bizonyítsuk be, hogy
(a) Ha az ABC háromszög szabályos, akkor a GKI háromszög is szabályos;
(b) Az ABC és XYZ háromszögek akkor és csak akkor hasonlók, ha az ABC háromszög szabályos.
Román versenyfeladat
(5 pont)
A. 435. Igazoljuk, hogy tetszőleges 1 a,b,c
a,b,c 2 számokra
2 számokra
Vietnami feladat
(5 pont)
A. 436. Bizonyítsuk be, hogy
tetszőleges pozitív egész n esetén.
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

