Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány

Már regisztráltál?
Új vendég vagy?

A KöMaL 2011. decemberi matematika feladatai

Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.

Feladat típusok elrejtése/megmutatása:

K-jelű feladatok

A beküldési határidő 2012. január 10-én LEJÁRT.

K. 313. Ha egy poharat ráfordítunk egy másik, ugyanolyan pohárra, akkor a következő esetek lehetségesek: ha két teteje, vagy két alja találkozik, akkor azok megállnak egymáson, ha viszont egy poháralj és egy pohártető, akkor azok egymásba csúsznak, és az együttes magasságuk másfél pohárnyi lesz. Zsolti pohártornyot készít: 9 db egyforma, felfelé néző poharat 3×3-as elrendezésbe letesz az asztalra, majd valamelyik függőleges vagy vízszintes szélső sorban lévő összes poharat a mellette fekvő sorban lévőkre ráfordítja, így 2×3-as elrendezéshez jut. Ezután ismét valamelyik függőleges vagy vízszintes szélső sort a mellette lévőre fordít, és így tovább, amíg egyetlen tornyot nem kap. Milyen magas lehet a torony?

(6 pont)

megoldás, statisztika

K. 314. Az ábrán az AQ, BR, CP, PM, QK és RL szakaszok felezőpontjai rendre P, Q, R, K, L és M.

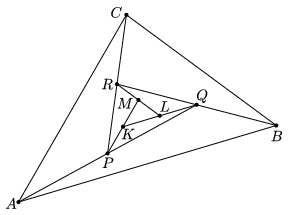
Mekkora a KLM háromszög területe, ha az ABC háromszög területe 441 cm²?

(6 pont)

megoldás, statisztika

K. 315. Jelölje $\downarrow\! n\! \downarrow$ az n-nél kisebb prímszámok közül a legnagyobbat, jelölje $\uparrow\! n\! \uparrow$ az n-nél nagyobb prímszámok közül a legkisebbet. Mennyi az alábbi kifejezés értéke?

$41+ \downarrow\! 35\! \downarrow - \uparrow\! 53\! \uparrow + \big\uparrow\! \downarrow\! 40\! \downarrow\! \big\uparrow$

(6 pont)

megoldás, statisztika

K. 316. Keressük meg az összes olyan pozitív közönséges törtet, amelyet a $\frac{12}{96}$ -hoz adva az összeg pontosan 1, és a két tört számlálójában és nevezőjében együtt minden számjegy pontosan egyszer szerepel.

(6 pont)

megoldás, statisztika

K. 317. Hány hegyesszög lehet egy konvex sokszög belső szögei között?

(6 pont)

megoldás, statisztika

K. 318. Bizonyítsuk be, hogy ha a, b, c, d egymást követő természetes számok, akkor d² osztója az a+b²+c³ összegnek.

(6 pont)

megoldás, statisztika

C-jelű feladatok

A beküldési határidő 2012. január 10-én LEJÁRT.

C. 1100. Írjunk a táblázat megfelelő mezőibe olyan számokat, amelyek az előre beírtakkal együtt minden sorban és minden oszlopban mértani sorozatok egymást követő elemei lesznek.

		12
144
			81
	288

(5 pont)

megoldás, statisztika

C. 1101. Egy játékboltban kilencesével csomagolt dobókockákat vásároltunk. Mindegyik csomagot ki kellett bontanunk ahhoz, hogy összeállítsunk egy tömör kockát. Hány darab kiskockánk maradhat az építkezés végén?

(5 pont)

megoldás, statisztika

C. 1102. Az ABC hegyesszögű háromszög C-ből induló magasságának talppontja D. Szerkesszük meg azt az AB-vel párhuzamos egyenest, aminek a háromszögbe eső szakasza D-ből derékszög alatt látszik.

Javasolta: Holló Gábor (Budapest)

(5 pont)

megoldás, statisztika

C. 1103. Gábor a szakkörön összeszorzott két pozitív számot. Érdekesnek találta, hogy ha a két számot összeadja, ugyanaz az eredmény. A számokat már elfelejtette, de arra emlékszik, hogy mindkét szám egyetlen tizedesjegyet tartalmazott. Melyek lehetnek ezek a számok?

(5 pont)

megoldás, statisztika

C. 1104. Egy hatszög minden szöge 120^o-os, az oldalai pedig váltakozva $\sqrt{3-\sqrt 3}$ , illetve $\sqrt{9-3\sqrt 3}$ hosszúságúak. Igazoljuk, hogy a hatszög területe egész.

(5 pont)

megoldás, statisztika

B-jelű feladatok

A beküldési határidő 2012. február 10-én LEJÁRT.

B. 4402. Egységnyi oldalú sötét négyzetbe fehér kört írunk, ebbe egy újabb sötét négyzetet, folytatva ezt az ábra szerint a végtelenségig. Mekkora a sötét részek területének összege?

(3 pont)

megoldás, statisztika

B. 4403. A 20×20-as sakktábla néhány mezőjén bábu áll. Egy bábut akkor vehetünk le a tábláról, ha annak sorában vagy oszlopában a mezőknek legalább a fele üres. Legfeljebb hány bábu lehet a táblán, ha ilyen lépések sorozatával az összeset le tudjuk venni?

(5 pont)

megoldás, statisztika

B. 4404. Az $A_1A_2 \ldots A_{2n}$ sokszög minden szöge egyenlő, oldalaira pedig teljesül, hogy $A_1A_2=A_3A_4=\ldots =A_{2n-1}A_{2n}$ és $A_2A_3=A_4A_5=\ldots = A_{2n}A_1$ . Mutassuk meg, hogy a sokszög köré kör írható.

(3 pont)

megoldás, statisztika

B. 4405. Az a és b nemnegatív számokra a³+b³=2ab teljesül. Következik-e ebből, hogy

a²+b² $\le$ 1+ab?

(4 pont)

megoldás, statisztika

B. 4406. Adottak az egymásra merőleges e₁ és e₂ egyenesek, valamint egyik szögfelezőjükön a metszéspontjuktól különböző P pont. A P-n átmenő f és g egyenesek az e_i egyenest az F_i, illetve G_i pontokban metszik. Határozzuk meg az F₁G₂ és F₂G₁ egyenesek metszéspontjának mértani helyét.

(4 pont)

megoldás, statisztika

B. 4407. Legyen k egy pozitív egész szám. Hány nemnegatív egész megoldása van az

$\Big[\frac xk\Big] = \Big[\frac x{k+1}\Big]$

egyenletnek?

(4 pont)

megoldás, statisztika

B. 4408. Az ABC háromszögben AC és BC oldalak hossza rögzített, a C-nél levő szög pedig változik. Az AC oldal felezőpontja M, a BC oldal felezőpontja N, az AB oldalra kifelé állított négyzet középpontja pedig O. Hogyan kell az ACB szöget megválasztani ahhoz, hogy az OM és ON távolságok összege a lehető legnagyobb legyen?

(4 pont)

megoldás, statisztika

B. 4409. Tegyük fel, hogy az n pozitív egész számra 2ⁿ+1 prím. Milyen maradékot adhat ez a prím 240-nel osztva?

(4 pont)

megoldás, statisztika

B. 4410. A matematika szakkörön a tanár gondolt egy legfeljebb n-ed fokú polinomfüggvényre. A diákok tetszőleges valós helyen megkérdezhetik a függvény helyettesítési értékét. Hány helyettesítési érték ismeretében dönthető el minden esetben, hogy a függvény páros-e?

(5 pont)

megoldás, statisztika

B. 4411. Két egyenes körkúp tengelye párhuzamos, a nyílásszögük különböző. Bizonyítsuk be, hogy közös pontjaik egy gömbön vannak.

(5 pont)

megoldás, statisztika

A-jelű feladatok

A beküldési határidő 2012. január 10-én LEJÁRT.

A. 548. Bizonyítsuk be, hogy

$\prod_{i=1}^n \left(1+\frac1{x_1+\ldots+x_i}\right) + \prod_{i=1}^n \left(1-\frac1{x_i+\ldots+x_n}\right) \le n+1$

teljesül tetszőleges $x_1,\ldots,x_n\ge 1$ valós számok esetén.

(5 pont)

megoldás, statisztika

A. 549. Az ABCD érintőnégyszög átlói az E pontban metszik egymást. Mutassuk meg, hogy az ABE, BCE, CDE és DAE háromszögekbe írt körök középpontjai egy körön vannak.

Javasolta: Holló Gábor (Budapest)

(5 pont)

A. 550. Igaz-e, hogy minden elég nagy pozitív egész szám előáll egy Fibonacci-szám és egy prímszám összegeként?

(5 pont)

megoldás, statisztika

A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:

megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.

(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)