KöMaL Problems in Mathematics, March 2013
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 10, 2013. |
K. 373. There are 29 coins lying on a table. Two players take turns removing coins from the table. In each step, the number of coins removed needs to be a positive square number. The player who can last remove some coin(s) will win the game. Which player has a winning strategy? (That is, which player can make sure that he will win the game whatever the moves of the other player are?)
(6 pont)
solution (in Hungarian), statistics
K. 374. In a triangle ABC, AB=28 cm, BC=38 cm. A perpendicular is dropped from A onto the interior angle bisector of the angle at B. The perpendicular intersects the angle bisector at F. The midpoint of side AC is F. What is the length of the line segment DF in centimetres?
(6 pont)
solution (in Hungarian), statistics
K. 375. A rectangle is divided into eight squares, as shown in the diagram. The area of the medium sized squares is 100 cm2. What is the area of the original rectangle?
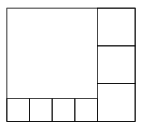
(6 pont)
solution (in Hungarian), statistics
K. 376. In how many different ways is it possible to select 3 out of the 16 points below, such that they are the vertices of a triangle?

(6 pont)
solution (in Hungarian), statistics
K. 377. A 100×100 cm square tablecloth is laid on a 120×120 cm square table, such that the centres of the two squares coincide, the sides of the tablecloth are parallel to the diagonals of the tabletop, and the corners of the tablecloth are hanging over the edges of the table. What is the area of the uncovered part of the tabletop?
(6 pont)
solution (in Hungarian), statistics
K. 378. Some friends had dinner in a restaurant, and decided to give a 15% tip to the waiter. If everyone pays 6000 forints (HUF, Hungarian currency) then the sum will be 2800 forints more than the price of the food but it will not cover the tip. If everyone pays 6600 forints then the sum will cover the tip, too, and they will get 1120 forints back. What was the total on the bill, and how many friends had dinner?
(6 pont)
 |
Problems with sign 'C'Deadline expired on April 10, 2013. |
C. 1160. What is the remainder if the sum 20122013+20132012 is divided by 2012.2013?
Suggested by D. Fülöp, Pécs
(5 pont)
solution (in Hungarian), statistics
C. 1161. The real numbers a, b, c in the equation satisfy a+b+c=0, abc=-48, and bc+ac+ab=-28. Solve the equation.
(5 pont)
solution (in Hungarian), statistics
C. 1162. A circle is drawn over the shorter diagonal AC=a of a parallelogram ABCD. The intersections of the circle and the parallelogram form the hexagon AIJCKL, whose sides have lengths , b, b,
, b, b in this order. Determine the sides and angles of the parallelogram.
(5 pont)
solution (in Hungarian), statistics
C. 1163. For what number pairs x, y will the numbers x, xlog x, ylog y, be consecutive terms of a geometric progression? (log denotes decimal logarithm.)
Suggested by A. Balga, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1164. ABCD is a square of area 2 dm2, and ABCDE is a right pyramid of height 3 dm. Let H be the point of edge AE lying closer to A that divides the edge 1:2, and let G be the point of edge CE lying closer to E that divides the edge 1:2. Let F be the midpoint of edge BE. Find the area of the intersection of the pyramid with the plane of triangle HFG.
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 10, 2013. |
B. 4522. Find all integers n such that |2n3-6n2+4n+3| is a prime.
(3 pont)
solution (in Hungarian), statistics
B. 4523. The diagonals of a symmetric trapezium are perpendicular to each other. What may be the ratio of the perimeter of the trapezium to its midline?
Suggested by B. Kovács, Szatmárnémeti
(4 pont)
solution (in Hungarian), statistics
B. 4524. f is a function defined on the set of natural numbers such that f(1)+22f(2)+32f(3)+...+n2f(n)=n3f(n) for all positive integers n. Given that f(1)=2013, find the value of f(2013).
Competition problem from Transsylvania
(4 pont)
solution (in Hungarian), statistics
B. 4525. Given n points in the interior of a regular triangle , prove that
can be covered with 2n+1 regular triangles whose sides are parallel to the sides of
such that they contain none of the n points in their interior. Also prove that the covering is not necessarily possible with 2n triangles.
Suggested by D. Pálvölgyi, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 4526. A wildfire spreads at a speed of 1 km/h in all directions. When the fire has burnt a circle of radius 1 km, an excavator arrives at the edge of the fire to dig a ditch to stop the spreading of the fire. The excavator can proceed at a maximum speed of 14 km/h. Find a possible path for the excavator such that the fire should not burn a total area greater than 13 km2.
Quantum
(4 pont)
solution (in Hungarian), statistics
B. 4527. In a dice game, the player rolls three dice simultaneously, and then he may roll two more times any number of his dice (0, 1, 2 or 3). The player wins the game if all three dice have the same number on top after the last roll. What is the best strategy, and with that strategy what is the probability of winning?
Suggested by E. Gáspár Merse, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4528. k is the circumscribed circle of a cyclic quadrilateral ABCD. The centre of the inscribed circle of triangle ABC is P, and that of triangle ABD is Q. Let E denote the midpoint of arc BC, and let F denote the midpoint of arc DA of the circle k. Prove that PQ is parallel to EF.
(5 pont)
solution (in Hungarian), statistics
B. 4529. Let n be a positive integer. Prove that .
(6 pont)
solution (in Hungarian), statistics
B. 4530. Prove that the midpoint of the line segment connecting the centres of two regular polygons of the same number of sides drawn on the sides AC and BC of a triangle ABC on the outside coincides with the centre of the regular polygon of the same number of sides drawn on the line segment connecting the midpoints of the sides AC and BC, on the side where the vertex C lies.
Suggested by Sz. Miklós, Herceghalom
(5 pont)
solution (in Hungarian), statistics
B. 4531. Solve the equation (x2+100)2=(x3-100)3.
Quantum
(5 pont)
 |
Problems with sign 'A'Deadline expired on April 10, 2013. |
A. 584. In 3-space, let S be a non-degenerate conic section which is not a circle. Consider the apices of those right circular conical surfaces that contain S. (a) Show that these points lie on a conic section, uniquely determined by S. (b) Denote by C(S) the conic section that contains the possible apices. Prove that C(C(S))=S for arbitrary S.
(5 pont)
A. 585. For some integer n 2 each pair (i,j), where 1
2 each pair (i,j), where 1 i,j
i,j n, is written on a card. We play the following game. The n2 cards are placed in an n×n table so that for every i and j, the card (i,j) is in the ith row, at the jth position. It is allowed to exchange the cards (i,j) and (k,l) if they are in the same row or in the same column, and i=k or j=l. Is it possible to reach that arrangement of the cards which contains (1,2) and (2,1) interchanged and all other cards are at their initial positions?
n, is written on a card. We play the following game. The n2 cards are placed in an n×n table so that for every i and j, the card (i,j) is in the ith row, at the jth position. It is allowed to exchange the cards (i,j) and (k,l) if they are in the same row or in the same column, and i=k or j=l. Is it possible to reach that arrangement of the cards which contains (1,2) and (2,1) interchanged and all other cards are at their initial positions?
Based on the idea of Zoltán Bertalan, Békéscsaba
(5 pont)
A. 586. Two convex quadrilaterals have side lengths a1, a2, a3, a4, and A1, A2, A3, A4; their areas are t and T, respectively. Show that
(The indices are used modulo 4.)
(5 pont)
Upload your solutions above.
