A KöMaL 2014. márciusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2014. április 10-én LEJÁRT. |
M. 340. Az ingyenesen letölthető Audacity hangelemző program segítségével határozzuk meg több különböző felület és egy pingponglabda közötti ütközési számot!
Közli: Simon Péter, Pécs
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2014. április 10-én LEJÁRT. |
P. 4616. A Tiszán edző evezősök sötétedés előtt másfél órával szállnak vízre. A Tisza vizének sebessége 3,6 km/h, a hajók a vízhez képest 6 m/s sebességgel haladnak. Milyen messzire mehetnek el az indulás helyétől, ha sötétedésre vissza kell érkezniük oda?
Tarján Imre fizikaverseny, Szolnok
(3 pont)
P. 4617. Egy diák kerékpárral ment Felsőnyergesről Vázfalvára. Azt tervezte, hogy 18 km/h átlagsebességgel fog haladni. A nagy forgalom miatt útja első harmadán csak 15 km/h volt az átlagsebessége.
a) Mekkora átlagsebességgel kellett haladnia a hátralevő távon, hogy terv szerint érjen célba?
b) Mekkora átlagsebességgel kellett haladnia a hátralevő időben, ha menetideje első harmadában haladt 15 km/h sebességgel?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4618. Három különböző tartályban 300 K, 500 K és 720 K hőmérsékletú levegő van. A 300 K-es és az 500 K-es gázok között megengedve a hőcserét a közös hőmérséklet 420 K, a 300 K-es és a 720 K-es gázok között megengedve a hőcserét a közös hőmérséklet 600 K lenne. Mennyi lenne akkor, ha az 500 K-es és a 720 K-es gázok hőmérséklete egyenlítődne ki? Hogyan aránylanak egymáshoz kezdetben a gázok belső energiái?
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(4 pont)
P. 4619. Mari egy 6 méter sugarú, egyenletesen forgó körhinta szélén ül. Máté a körhinta középpontjától 12 méterre a földön áll. Máté úgy látja, hogy Mari éppen feléje mozog 1 m/s sebességgel. Mekkora sebességgel mozgónak látja Mari Mátét?
Amerikai feladat nyomán
(4 pont)
P. 4620. Egy r=10 cm sugarú, homogén gömb vízszintes síkon rögzített R=2r sugarú félgömb tetejéről kezdősebesség nélkül legördül. A két gömb közötti súrlódási tényező μ=0,2.
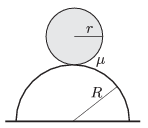
a) Hol csúszik meg a legördülő gömb?
b) Mekkora a megcsúszás pillanatában a gömb középpontjának sebessége?
Közli: Holics László, Budapest
(5 pont)
P. 4621. Ideális gáz az ábrán látható folyamaton megy át. A kezdőállapotban V1=2 dm3, p1=105 Pa, T1=300 K. A végállapotban V2=8 dm3, p2=2,5⋅104 Pa. Mekkora a gáz legmagasabb hőmérséklete a folyamat során, és ezt melyik állapotban éri el?
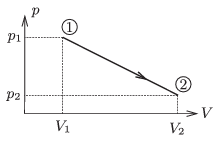
Közli: Légrádi Imre, Sopron
(4 pont)
P. 4622. N=100 darab egyforma galvánelemet az ábrán látható módon teleppé kapcsolunk össze. Mindegyik galvánelem üresjárati feszültsége U0, belső ellenállása Rb.
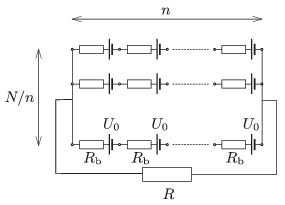
Milyen elrendezés esetén adja le ez a telep a legnagyobb teljesítményt egy külső R ellenálláson, ha
a) R=Rb;
b) R=4Rb;
c) R=5Rb?
Közli: Radnai Gyula, Budapest
(5 pont)
P. 4623. Súlypontján átmenő forgástengellyel ellátott mágnestű percenként 24-et leng, ha forgástengelye függőleges. Hányat leng percenként, ha forgástengelye vízszintes és
a) párhuzamos a mágneses délvonallal;
b) merőleges a mágneses délvonalra?
Az észlelés helyén a mágneses lehajlás 60∘.
Faragó Andor (1877-1944) feladata
(5 pont)
P. 4624. A mikrohullámú sütőbe gondatlanságból behelyezett villa ágai között szikrázást figyeltünk meg. A villa ágai 5 cm hosszúak voltak, közöttük 4 mm-es résekkel. Az elektromágneses tér frekvenciája 2,45 GHz volt. Becsüljük meg, mekkora lehetett a mágneses indukcióvektor nagysága a villa helyén! (A levegőben a szikra átütéséhez körülbelül 3 kV/mm elektromos térerősség szükséges.)
Közli: Bilicz Sándor, Budapest
(4 pont)
P. 4625. A Napnak gyűjtőlencsével előállított képét fehér ernyőn fogjuk fel. Milyen adatokra van szükségünk, hogy megmondhassuk, hogy a Nap képe az ernyőn hányszor fényesebb, mint az ernyőnek a Nap által közvetlenül megvilágított része?
Selényi Pál (1884-1954) feladata
(4 pont)
P. 4626. Két egyforma, r sugarú, kezdetben töltetlen vezető gömb egymástól d≫r távolságra helyezkedik el az ábra szerint.
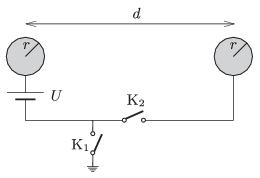
a) Zárjuk a K2 kapcsolót. Mekkora erő ébred a gömbök között?
b) Mekkora erő ébredne a gömbök között, ha az előző kísérletben a K2 kapcsoló helyett a K1 kapcsolót zárnánk?
c) Határozzuk meg a gömbök közötti erőt, ha mindkét kapcsolót zárjuk!
Közli: Vigh Máté, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

