A KöMaL 2014. áprilisi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2014. május 12-én LEJÁRT. |
M. 341. Néhány tojás fehérjéjét verjük kemény habbá! Mérjük meg, hányszorosára nőtt a tojásfehérje térfogata! Mekkora a keletkezett buborékok átlagos mérete? Becsüljük meg a buborékok számát!
Közli: Vass Miklós, Budapest
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2014. május 12-én LEJÁRT. |
P. 4627. Egy felfújt lufit két tenyerünk közé fogva előbb-utóbb azt érezzük, hogy a lufi melegíti a kezünket. Hogy lehet ez?
Kérdezi: Radnai Réka, Budapest, Andor Ilona Ének-Zenei Ált. Isk.
(3 pont)
P. 4628. A 4-es számű főúton haladó gépkocsi a Szolnok és Kisújszállás közötti 50 km-es utat 75 km/h, a Kisújszállás és Karcag közötti 10 km-es utat 80 km/h átlágsebességgel tette meg. Beérhet-e Szolnokról Debrecenbe másfél óra alatt ez a gépkocsi, ha a Karcag és Debrecen közötti 64 km-es úton sem lehet a sebessége 90 km/h-nál nagyobb?
Tarján Imre fizikaverseny, Szolnok
(3 pont)
P. 4629. Vízszintes, súrlódásos talajon egy mozgásában magára hagyott test mozgási energiája egy adott pillanatban 900 J, 2 s múlva már csak 400 J, miközben a test ℓ utat tesz meg.
a) Az ℓ út hányszorosát teszi meg még a test a megállásig?
b) Mennyi idő alatt teszi meg ezt az utat?
Közli: Dudics Pál, Debrecen
(4 pont)
P. 4630. Egy zsáknyi homok vízszintes felületen egy könnyű szőnyegen fekszik. Az M tömegű zsákot a szőnyeg segítségével lassan át akarjuk húzni egy viszonylag sima felületről egy érdesebb felületre. Mennyi munkát kell végeznünk, ha a felületek és a szőnyeg közötti súrlódási együttható μ1, illetve μ2? A zsák súlya nem egyenletesen oszlik el a szőnyegen, de tudjuk, hogy a tömegközéppontja a széleitől s1, illetve s2 távolságban van. (Lásd még a P. 4554. megoldott feladatot lapunk 237. oldalán!)
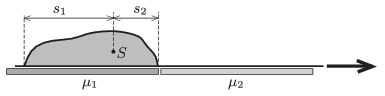
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 4631. Vízszintes, sima jégre állított kétszárú létra szárai α=60∘-os szöget zárnak be egymással. Az m=5 kg tömegű, L=2 m hosszú szárakat összekötő csukló súrlódásmentes. A vékony, kezdetben feszes biztonsági kötél elszakad.
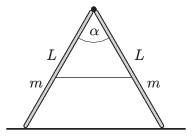
a) Mekkora szöget zárnak be egymással a létraszárak abban a pillanatban, amikor a csukló nem fejt ki erőt?
b) Mekkora erővel nyomja ekkor a létra a jeget?
c) Mekkora sebességgel érkezik a jégre a csukló?
(A létraszárakat a tehetetlenségi nyomaték szempontjából tekintsük vékony, homogén rudaknak!)
Közli: Holics László, Budapest
(5 pont)
P. 4632. Adott tömegű légritkított gázt az ábrán megadott A állapotból az AB úton a B állapotba viszünk. Mennyi munkát végzünk eközben?
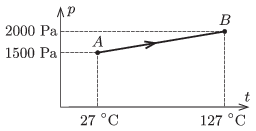
Közli: Simon Ferenc, Zalaegerszeg
(4 pont)
P. 4633. Bizonyos tömegű egyatomos ideális gázzal működő hőerőgép az ábrán látható ABCA vagy ADEA körfolyamatot végezheti. Mekkora a kétféle hatásfok aránya?
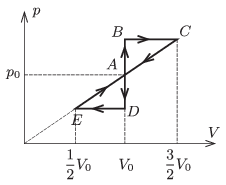
Közli: Kotek László, Pécs
(5 pont)
P. 4634. Egy a=12 cm oldalú szabályos hatszög ábra szerinti két csúcsában Q=6,4⋅10−8 C töltés, a velük szemközti csúcsban −Q töltés van. Milyen irányú és mekkora az elektromos térerősség a hatszög középpontjában és a hatszög töltésmentes csúcsaiban?
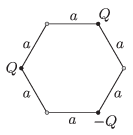
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4635. Mekkora az ábrán látható kapcsolásban R értéke, ha a kondenzátor feszültsége
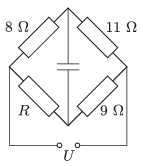
a) UC=0;
b) UC=U2?
Közli: Légrádi Imre, Sopron
(4 pont)
P. 4636. Egy optikai rácsot alkotó rések szélessége a rácsállandó n-ed része. Monokromatikus, λ hullámhosszúságú lézerfénnyel merőlegesen világítjuk meg a d rácsállandójú rácsot, és egy L≫d távolságra lévő ernyőn vizsgáljuk a diffrakciós (elhajlási) képet. Adjuk meg az elhajlási vonalak helyzetét az ernyőn!
Közli: Woynarovich Ferenc, Budapest
(5 pont)
P. 4637. Szigetelő szálra függesztett, alufóliával bevont csokoládényuszit elektromosan feltöltünk. A nyuszi a levegő csekély vezetőképessége miatt lassan elveszíti a töltését. Milyen lesz kisülés közben a nyuszi körül kialakuló mágneses mező? (Feltehetjük, hogy a levegő vezetőképessége független a helytől.)

Közli: Vigh Máté, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

