KöMaL Problems in Mathematics, May 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on June 10, 2015. |
C. 1294. Express the fraction \(\displaystyle \frac{13}{38}\) in the form \(\displaystyle \frac 1m+\frac 1n\), where \(\displaystyle m\) and \(\displaystyle n\) are positive integers.
(5 pont)
C. 1295. The angles at vertices \(\displaystyle C\) and \(\displaystyle D\) of a quadrilateral \(\displaystyle ABCD\) are equal, and the intersection \(\displaystyle E\) of the interior angle bisectors drawn at vertices \(\displaystyle A\) and \(\displaystyle B\) lies on the side \(\displaystyle CD\). Prove that \(\displaystyle E\) bisects side \(\displaystyle CD\).
(5 pont)
C. 1296. Find the angles of the acute-angled isosceles triangle in which the reflection of the centroid about the foot of an altitude lies on the line of the base.
(5 pont)
C. 1297. The main attractions of the show in a circus are the performances of a lion and an elephant. However, these performances cannot be accomplished if the animals are not in the mood. The lion appears on stage in \(\displaystyle \frac{4}{5}\) of the shows, and the elephant only appears in \(\displaystyle \frac{3}{4}\) of the shows. The circus is so lucky as to be able to show at least one of the animals in \(\displaystyle 99\%\) of the shows. What is the probability of both animals appearing in a show?
(5 pont)
C. 1298. The accompanying diagram shows a park with line segments representing the footpaths (in the diagram ``Bejárat'' = ``Entrance'', ``Kijárat'' = ``Exit''). In how many ways is it possible to get from the entrance to the exit if it is not allowed to leave the footpaths, and each footpath is walked at most once?
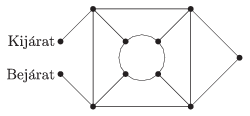
(5 pont)
C. 1299. Solve the equation \(\displaystyle x^3+(1-3b)x^2 + \big(3b^2+2b-6\big) x-b^3+b^2-6b+9=0\), if \(\displaystyle x-b\ge 0\).
(5 pont)
C. 1300. The lengths of the sides of a convex quadrilateral, in this order, are \(\displaystyle \sqrt{a}\), \(\displaystyle \sqrt{a+3}\), \(\displaystyle \sqrt{a+2}\) and \(\displaystyle \sqrt{2a+5}\). The length of each diagonal is \(\displaystyle \sqrt{2a+5}\). Determine the greatest angle of the quadrilateral.
(5 pont)
 |
Problems with sign 'B'Deadline expired on June 10, 2015. |
B. 4714. Given 2015 points in the plane, show that if every four of them form a convex quadrilateral then the points are the vertices of a convex 2015-sided polygon.
(4 pont)
B. 4715. Find all pairs of positive integers \(\displaystyle (a,b)\) such that \(\displaystyle a^{(b^2)}=b^a\).
(5 pont)
B. 4716. The rhombus \(\displaystyle ABFE\) determined by sides \(\displaystyle AB\) and \(\displaystyle AE\) is cut out of a regular pentagon \(\displaystyle ABCDE\). Determine the centre of mass of the remaining concave pentagonal plate \(\displaystyle BCDEF\).
Suggested by P. Dombi, Pécs
(3 pont)
B. 4717. Solve the equation \(\displaystyle |1-x| = \left|2x-57-2\sqrt{x-55} +\frac{1}{x-54-2\sqrt{x-55}}\right|\).
Suggested by B. Bíró, Eger
(4 pont)
B. 4718. The midpoint of edge \(\displaystyle B'C'\) of a cube \(\displaystyle ABCDA'B'C'D'\) is \(\displaystyle E\), and the midpoint of edge \(\displaystyle C'D'\) is \(\displaystyle F\). The plane \(\displaystyle AEF\) divides the cube into two parts. Find the ratio of the volumes of the two parts.
(5 pont)
B. 4719. Show that
\(\displaystyle \sum_{j=0}^{b}\, \sum_{i=j}^{a-b+j} \binom{i}{j} \binom{a-i}{b-j} =(a+1)\binom{a}{b} \)
for all positive integers \(\displaystyle a \ge b\).
Suggested by I. Porupsánszki, Miskolc
(5 pont)
B. 4720. Let \(\displaystyle a\) and \(\displaystyle n\) denote positive integers such that \(\displaystyle a^n-1\) is divisible by \(\displaystyle n\). Prove that the numbers \(\displaystyle a+1\), \(\displaystyle a^2+2\), ..., \(\displaystyle a^n+n\) all leave different remainders when divided by \(\displaystyle n\).
(6 pont)
B. 4721. A circle \(\displaystyle k\) touches the legs \(\displaystyle AB\) and \(\displaystyle AC\) of an isosceles triangle \(\displaystyle ABC\), and intersects the base \(\displaystyle BC\) at \(\displaystyle K\) and \(\displaystyle L\). Line segment \(\displaystyle AK\) intersects the circle \(\displaystyle k\) again at point \(\displaystyle M\). The reflections of point \(\displaystyle K\) in \(\displaystyle B\) and in \(\displaystyle C\) are \(\displaystyle P\) and \(\displaystyle Q\), respectively. Prove that \(\displaystyle k\) is tangent to the circumscribed circle of triangle \(\displaystyle PMQ\).
(6 pont)
B. 4722. Each permutation of an \(\displaystyle n\)-element set is coloured in either red, white or green. Let \(\displaystyle N_{\rm RWG}\) denote the number of ways to perform a red permutation followed by a white permutation and then a green permutation, such that each element is restored to its initial position at the end. Analogously, let \(\displaystyle N_{\rm GWR}\) denote the number of ways to perform a green permutation followed by a white permutation and then finally a red permutation, such that each element is restored to its initial position. Show that \(\displaystyle N_{\rm RWG}=N_{\rm GWR}\).
(6 pont)
 |
Problems with sign 'A'Deadline expired on June 10, 2015. |
A. 644. Let \(\displaystyle f(x,y)\) be a polynomial with two variables and integer coefficients such that \(\displaystyle f\) is constant neither in \(\displaystyle x\)- nor in \(\displaystyle y\)-direction. Prove that \(\displaystyle \max_{a,b\in[-2,2]}\big|f(a,b)\big|\ge4\).
Based on the idea of Tamás Erdélyi, College Station, Texas
(5 pont)
A. 645. Do there exist infinitely many (not necessarily convex) 2015-gons in the plane such that every three of them have a common interior point, but no four have a common point?
(5 pont)
A. 646. Ginger and Rocky play the following game. First Ginger hides two bones in the corners of a rectangular garden. She may dig 45 cm deep altogether, that is, she may either hide the two bones in two different corners, where the sum of their depths may be at most 45 cm, or she may hide them in the same place, both bones at a maximum depth of 45 cm. She levels the ground carefully so that it is impossible to see where she has dug. Then Rocky may dig holes with a total depth of 1 m. Rocky's goal is to maximize the probability of finding both bones, while Ginger's goal is to maximize the probability of keeping at least one for herself.
\(\displaystyle (a)\) Show that if Ginger plays well she can achieve a probability of more than \(\displaystyle 1/2\) for at least one bone remaining hidden, independently of Rocky's search strategy.
\(\displaystyle (b)\) What are the chances of Ginger's success if both dogs play optimally?
Proposed by: Endre Csóka, Warwick
(5 pont)
Upload your solutions above.
