A KöMaL 2015. májusi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
C-jelű feladatokA beküldési határidő 2015. június 10-én LEJÁRT. |
C. 1294. Fejezzük ki a \(\displaystyle \frac{13}{38}\) törtet \(\displaystyle \frac 1m+\frac 1n\) alakban, ahol \(\displaystyle m\) és \(\displaystyle n\) pozitív egész számok.
(5 pont)
C. 1295. Az \(\displaystyle ABCD\) négyszög \(\displaystyle C\) és \(\displaystyle D\) csúcsánál levő szög megegyezik, továbbá az \(\displaystyle A\) és \(\displaystyle B\) csúcsnál levő belső szögfelezők \(\displaystyle E\) metszéspontja a \(\displaystyle CD\) oldalra esik. Bizonyítsuk be, hogy \(\displaystyle E\) felezi a \(\displaystyle CD\) oldalt.
(5 pont)
C. 1296. Mekkorák annak a hegyesszögű egyenlőszárú háromszögnek a szögei, melynek súlypontját az egyik magasság talppontjára tükrözve a tükörkép a háromszög alapjának egyenesére esik?
(5 pont)
C. 1297. Egy cirkuszban a fő attrakció az oroszlán és az elefánt mutatványa. Az állatok szeszélyessége miatt azonban nem mindig valósítható meg ez a két produkció. Az oroszlán az előadások \(\displaystyle \frac{4}{5}\) részében lép porondra, míg az elefánt csak \(\displaystyle \frac{3}{4}\) részében. Szerencsés cirkusz lévén, az előadások \(\displaystyle 99\%\)-ában legalább az egyik állat szerepel. Mekkora valószínűséggel láthatjuk mindkét állatot egy műsoron?
(5 pont)
C. 1298. A mellékelt ábra egy parkot szemléltet, ahol a szakaszok mutatják az ösvényeket. Hányféleképpen juthatunk el a bejárattól a kijáratig, ha minden ösvényen legfeljebb egyszer mehetünk végig, és az ösvényekről nem térhetünk le?
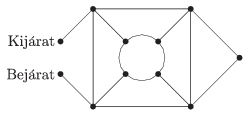
(5 pont)
C. 1299. Oldjuk meg az \(\displaystyle x^3+(1-3b)x^2 + \big(3b^2+2b-6\big) x-b^3+b^2-6b+9=0\) egyenletet, ha \(\displaystyle x-b\ge 0\).
(5 pont)
C. 1300. Egy konvex négyszög oldalainak hossza sorban \(\displaystyle \sqrt{a}\), \(\displaystyle \sqrt{a+3}\), \(\displaystyle \sqrt{a+2}\) és \(\displaystyle \sqrt{2a+5}\), mindkét átlója \(\displaystyle \sqrt{2a+5}\) hosszú. Határozzuk meg a négyszög legnagyobb szögét.
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2015. június 10-én LEJÁRT. |
B. 4714. Adott a síkon 2015 pont. Mutassuk meg, hogy ha közülük bármely négy egy konvex négyszög négy csúcsa, akkor a pontok egy konvex 2015-szög csúcsai.
(4 pont)
B. 4715. Adjuk meg az összes pozitív egész számokból álló \(\displaystyle (a,b)\) számpárt, amelyre \(\displaystyle a^{(b^2)}=b^a\) teljesül.
(5 pont)
B. 4716. Az \(\displaystyle ABCDE\) szabályos ötszögből kivágtuk az \(\displaystyle AB\) és \(\displaystyle AE\) élek által meghatározott \(\displaystyle ABFE\) rombuszt. Határozzuk meg a megmaradó \(\displaystyle BCDEF\) konkáv ötszöglemez súlypontját.
Javasolta: Dombi Péter (Pécs)
(3 pont)
B. 4717. Oldjuk meg az
\(\displaystyle |1-x| = \left|2x-57-2\sqrt{x-55}+\frac{1}{x-54-2\sqrt{x-55}}\right| \)
egyenletet.
Javasolta: Bíró Bálint (Eger)
(4 pont)
B. 4718. Az \(\displaystyle ABCDA'B'C'D'\) kocka \(\displaystyle B'C'\) élének felezőpontja \(\displaystyle E\), \(\displaystyle C'D'\) élének felezőpontja pedig \(\displaystyle F\). Az \(\displaystyle AEF\) sík két részre osztja a kockát. Határozzuk meg a két rész térfogatának arányát.
(5 pont)
B. 4719. Bizonyítsuk be, hogy bármely \(\displaystyle a \ge b\) pozitív egész számokra teljesül, hogy
\(\displaystyle \sum_{j=0}^{b}\, \sum_{i=j}^{a-b+j} \binom{i}{j} \binom{a-i}{b-j} =(a+1)\binom{a}{b}. \)
Javasolta: Porupsánszki István (Miskolc, Földes Ferenc Gimn., 12. évf.)
(5 pont)
B. 4720. Figyelem! A feladat szövege a nyomtatott lapban hibásan jelent meg.
Legyenek \(\displaystyle a\) és \(\displaystyle n\) olyan pozitív egészek, amelyekre \(\displaystyle a^n-1\) osztható \(\displaystyle n\)-nel. Bizonyítsuk be, hogy az \(\displaystyle a+1\), \(\displaystyle a^2+2\), ..., \(\displaystyle a^n+n\) számok mind különböző maradékot adnak \(\displaystyle n\)-nel osztva.
(6 pont)
B. 4721. A \(\displaystyle k\) kör érinti az \(\displaystyle ABC\) egyenlő szárú háromszög \(\displaystyle AB\) és \(\displaystyle AC\) szárait, a \(\displaystyle BC\) alapját pedig \(\displaystyle K\)-ban és \(\displaystyle L\)-ben metszi. Az \(\displaystyle AK\) szakasz a \(\displaystyle k\) kört másodszor az \(\displaystyle M\) pontban metszi. A \(\displaystyle K\) pont \(\displaystyle B\)-re, illetve \(\displaystyle C\)-re vonatkozó tükörképe rendre \(\displaystyle P\) és \(\displaystyle Q\). Igazoljuk, hogy \(\displaystyle k\) érinti a \(\displaystyle PMQ\) háromszög köré írt kört.
(6 pont)
B. 4722. Egy \(\displaystyle n\)-elemű halmaz minden permutációját kiszíneztük a piros, fehér és zöld színek valamelyikével. Jelölje \(\displaystyle N_{PFZ}\) azt, hogy hányféleképpen lehet egymás után egy piros, majd egy fehér, végül egy zöld permutációt végrehajtani úgy, hogy végül minden elem a helyére kerüljön vissza. Hasonlóan, jelölje \(\displaystyle N_{ZFP}\) azt, hogy hányféleképpen lehet egymás után egy zöld, egy fehér, végül egy piros permutációt végrehajtani úgy, hogy végül minden elem a helyére kerüljön vissza. Mutassuk meg, hogy \(\displaystyle N_{PFZ}=N_{ZFP}\).
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2015. június 10-én LEJÁRT. |
A. 644. Legyen \(\displaystyle f(x,y)\) kétváltozós, egész együtthatós polinom, ami sem \(\displaystyle x\)-, sem \(\displaystyle y\)-irányban nem konstans. Mutassuk meg, hogy
\(\displaystyle \max_{a,b\in[-2,2]}\big|f(a,b)\big|\ge4. \)
Erdélyi Tamás (College Station, Texas) ötletéből
(5 pont)
A. 645. Létezik-e végtelen sok (nem feltétlenül konvex) 2015-szög a síkon úgy, hogy közülük bármely háromnak van közös belső pontja, de semelyik négynek nincs közös belső pontja?
(5 pont)
A. 646. Pamacs és Cézár a következő játékot játssza. Először Pamacs két csontot elás a téglalap alakú kert sarkaiban. Összesen 45 cm mélyre áshat, tehát a két csontot vagy különböző sarokba rejti, és a mélységeik összege legfeljebb 45 cm, vagy pedig egy helyre, és mindkét csontnak legfeljebb 45 cm mélyen kell lennie. A földet gondosan elsimítja, így nem lehet ránézésre megállapítani, hogy mely sarkokba rejthette el a csontokat. Cézár ezek után gödröket áshat ki, melyek mélységének összege összesen 1 m. Cézár célja az, hogy minél nagyobb eséllyel megtalálja mindkét csontot, Pamacs célja pedig az, hogy minél nagyobb valószínűséggel megtarthassa magának legalább az egyiket.
\(\displaystyle (a)\) Mutassuk meg, hogy Pamacs ügyesen játszva elérheti, hogy 1/2-nél nagyobb valószínűséggel rejtve maradjon legalább az egyik csontja, függetlenül Cézár stratégiájától.
\(\displaystyle (b)\) Ha mindkét kutya optimálisan játszik, Pamacs mekkora eséllyel jár sikerrel?
Javasolta: Csóka Endre (Warwick)
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)