A KöMaL 2016. januári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2016. február 10-én LEJÁRT. |
K. 487. Keressük meg azt a legnagyobb, illetve legkisebb nyolcjegyű számot, melynek számjegyei 0, 1, 2, 3, 4, 5, 6, 7 valamilyen sorrendben, és teljesül rá, hogy bármely két szomszédos számjegyének összege prímszám.
(6 pont)
K. 488. Bizonyítsuk be, hogy ha \(\displaystyle a \ge n\), továbbá \(\displaystyle a\) és \(\displaystyle n\) pozitív egész számok, akkor az
\(\displaystyle (a-1)(a-2)(a-3)\ldots (a-n) \)
szorzat osztható \(\displaystyle n\)-nel.
(6 pont)
K. 489. Péter beírta az első 2015 pozitív egész számot egy \(\displaystyle 100\times 100\)-as táblázatba az ábrának megfelelően. (Az ábrán látható kitöltés még nem teljes.) Melyik számot írta a 2. sorban utolsóként?
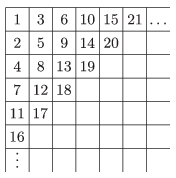
(6 pont)
K. 490. Anti hangyákat idomít. A mutatványa a következő: 99 hangya alszik egy 1 m hosszú egyenes rúdon. Füttyszóra egyszerre felébrednek, és elindulnak a rúd valamelyik vége felé 1 cm/s sebességgel. Ha egy hangya a rúd végére ér, lemászik a rúdról. Ha két hangya találkozik, mindketten azonnal megfordulnak és az ellenkező irányba indulnak tovább. A műsorszám addig tart, amíg minden hangya le nem mászik a rúdról. Legfeljebb mennyi ideig tarthat a mutatvány?
(6 pont)
K. 491. András gondolt öt számra és felírta őket egy lapra. A számokból képezte az összes lehetséges háromtagú összeget. Így a következő értékeket kapta: 3, 4, 6, 7, 9, 10, 11, 14, 15 és 17. Melyik öt számra gondolt András?
(6 pont)
K. 492. Hány olyan legfeljebb négyjegyű pozitív egész szám van, melyben a számjegyek összege legfeljebb 31?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2016. február 10-én LEJÁRT. |
C. 1329. Szaniszló király udvarából küldöttség indul egy távoli fejedelemségbe. Három nap után egy futárt visszaküldenek az udvarba egy üzenettel. A futár két nap alatt teszi meg azt az utat, amelyet a küldöttség három nap alatt. A válasszal a futár a küldöttség után nyargal, és pontosan akkor éri utol őket, amikor azok megérkeznek a fejedelemségbe. A fejedelmet viszont, Szaniszló király nagy barátját, közben száműzték. Ezért az egész küldöttség nyomban visszafordul, de most már mindannyian a futár sebességével mennek haza. Hány nap telik el a küldöttség indulása és visszaérkezése között?
(5 pont)
C. 1330. Hány különböző, téglalap alakú montázst készíthetünk négy különböző, \(\displaystyle 2:3\) képarányú fotóból? (A fényképeket nagyíthatjuk, de nem forgathatjuk el, és két montázst ugyanolyannak tekintünk, ha nagyítással megkaphatóak egymásból.)
(5 pont)
C. 1331. Peti a 13 éves születésnapi zsúrjára 13 barátját hívta meg. Mindegyiküktől 13 darab színes tömbgyertyát kapott, melyek 2,5 cm sugarú, 30 cm magasságú, szabályos henger alakúak. Hogy épségben megőrizhesse kincseit, elővesz egy \(\displaystyle \rm 50~cm \times 78~cm \times 31~cm\) nagyságú, téglatest alakú dobozt. Be tudja-e rakni Peti a gyertyákat a dobozba úgy, hogy azok ne sérüljenek, és egyik se lógjon ki a dobozból?
(5 pont)
C. 1332. Viktória nagymamája az ötöslottón minden héten egy szelvénnyel játszik. Mekkora a valószínűsége annak, hogy egy év alatt (52 húzás során) egyszer sem nyer? (Az ötöslottón 90 szám közül 5 nyerőszámot sorsolnak ki. Egy nyertes szelvényen ezek közül legalább 2 számot kell eltalálni.)
(5 pont)
C. 1333. Határozzuk meg azt a háromelemű, valós számokból álló adathalmazt, amelynek átlaga, mediánja és szórása is 3.
(5 pont)
C. 1334. Bizonyítsuk be, hogy ha az \(\displaystyle ABCD\) húrnégyszög trapéz (ahol \(\displaystyle AB\parallel CD\)) vagy az \(\displaystyle AB\) oldala a köréírt kör átmérője, akkor teljesülnek a
\(\displaystyle BD\cdot x+AD\cdot \sqrt{1-x^2} = AC;\)
\(\displaystyle AC\cdot x+BC\cdot \sqrt{1-x^2} = BD\)
egyenletek valamely \(\displaystyle 0<x<1\) esetén.
(5 pont)
C. 1335. Egy egységnyi oldalú, szabályos háromszög alapú gúla oldaléleinek hossza 2 egység. Mekkora a gúla kitérő éleinek távolsága?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2016. február 10-én LEJÁRT. |
B. 4759. Egy kerek asztal körül négy férfi és négy nő ül. Bizonyítsuk be, hogy van négy szomszédos ember, akik közt ugyanannyi a nő, mint a férfi.
(3 pont)
B. 4760. Négy különböző színű, szabályos dobókockát elhelyeztünk egymás mellett, az ábrán látható módon. Egy lépésben a következőt tehetjük: megfogunk két lapszomszédos kockát, és ezeket a közös lap középpontján átmenő, arra merőleges tengely körül \(\displaystyle 90^\circ\)-kal elforgatjuk. Hányféle különböző elrendezést lehet létrehozni ilyen lépésekkel?
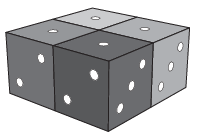
(6 pont)
B. 4761. Legyen az \(\displaystyle n\) egész 3-nál nagyobb. Igazoljuk, hogy ha egy egész szám \(\displaystyle n\) alapú számrendszerbeli alakjában minden számjegy pontosan egyszer fordul elő, akkor a szám nem lehet prímszám.
Javasolta: Halasi Zoltán (Csobánka)
(4 pont)
B. 4762. Egy egyszerű gráfnak minden csúcsa negyedfokú, és minden éléhez pontosan egy olyan csúcs található, amely az él mindkét végpontjával össze van kötve. Legalább hány csúcsa van egy ilyen gráfnak?
(3 pont)
B. 4763. Legyen \(\displaystyle G\) egy \(\displaystyle n\) csúcsú, irányítatlan, egyszerű gráf. Igazoljuk, hogy megadhatóak a gráfhoz a természetes számok olyan végtelen \(\displaystyle \mathcal{H}_1,\mathcal{H}_2, \ldots, \mathcal{H}_n\) részhalmazai, amelyekre bármely két részhalmaz metszete végtelen, ha a hozzájuk tartozó csúcsok éllel összekötöttek, és üres, ha nincs él a megfelelő csúcsok között.
Javasolta: Mészáros Gábor (Budapest)
(4 pont)
B. 4764. Tekintsük a síkbeli derékszögű koordináta-rendszerben az összes olyan egyenest, amelynek az egyenlete felírható \(\displaystyle aX+\frac{Y}{a}=2\) alakban, ahol \(\displaystyle a\) valós szám. Határozzuk meg a sík azon pontjainak halmazát, amelyek egyik egyenesen sincsenek rajta.
(5 pont)
B. 4765. Az \(\displaystyle ABCD\) húrnégyszögben az \(\displaystyle ADB\sphericalangle\) és \(\displaystyle ACB\sphericalangle\) szögek felezői az \(\displaystyle AB\) oldalt rendre az \(\displaystyle E\) és \(\displaystyle F\) pontokban, a \(\displaystyle CBD\sphericalangle\) és \(\displaystyle CAD\sphericalangle\) szögek felezői pedig a \(\displaystyle CD\) oldalt rendre a \(\displaystyle G\) és \(\displaystyle H\) pontokban metszik. Bizonyítsuk be, hogy az \(\displaystyle E\), \(\displaystyle F\), \(\displaystyle G\), \(\displaystyle H\) pontok egy körön vannak.
Javasolta: Bíró Bálint (Eger)
(6 pont)
B. 4766. Az \(\displaystyle a_{1}, a_{2}, \ldots\) sorozatot a következő rekurzióval definiáljuk: \(\displaystyle a_{1}=1\), \(\displaystyle a_{2}=5\), \(\displaystyle a_{3}=15\), továbbá ha \(\displaystyle n\ge 4\), akkor
\(\displaystyle a_{n}=n^{2}+a_{n-1}+a_{n-2}-a_{n-3}. \)
\(\displaystyle a)\) Számítsuk ki az \(\displaystyle a_{1}+a_{2}+a_{3}+\ldots +a_{2015}\) összeget.
\(\displaystyle b)\) Igazoljuk, hogy \(\displaystyle \frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}+ \ldots +\frac{1}{a_{2015}}<\frac{4}{3}\).
Javasolta: Kovács Béla (Szatmárnémeti)
(5 pont)
B. 4767. Határozzuk meg azokat a konvex poliédereket, amelyekre teljesül, hogy mindegyik \(\displaystyle C\) csúcs körül a csatlakozó lapok \(\displaystyle C\)-nél levő szögeinek összege pontosan \(\displaystyle 180^\circ\).
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2016. február 10-én LEJÁRT. |
A. 659. Mely \(\displaystyle n\) pozitív egész számokhoz találhatók olyan \(\displaystyle g(x)\) és \(\displaystyle h(x)\) valós együtthatós, \(\displaystyle n\)-nél alacsonyabb fokú polinomok, amelyekkel
\(\displaystyle g\big(h(x)\big) =x^n+x^{n-1}+x^{n-2}+\ldots+x^2+x+1? \)
Schweitzer Miklós Emlékverseny, 2015
(5 pont)
A. 660. Az \(\displaystyle ABCD\) érintőnégyszög beírt köre \(\displaystyle \omega\), az \(\displaystyle ABC\) és az \(\displaystyle ACD\) háromszögekbe írt körök középpontjai \(\displaystyle I\), illetve \(\displaystyle J\). Legyen \(\displaystyle T\) és \(\displaystyle U\) az a két pont az \(\displaystyle \omega\) körnek az \(\displaystyle ABC\), illetve az \(\displaystyle ACD\) háromszögbe eső ívén, amelyre az \(\displaystyle ATC\), illetve az \(\displaystyle ACU\) körök érintik \(\displaystyle \omega\)-t. Mutassuk meg, hogy az \(\displaystyle AC\), \(\displaystyle IU\) és \(\displaystyle JT\) szakaszok egy ponton mennek át.
(5 pont)
A. 661. Legyen \(\displaystyle K\) rögzített pozitív egész szám. Legyen \(\displaystyle (a_0,a_1,\ldots)\) az a számsorozat, amelyre \(\displaystyle a_0=-1\) és bármely \(\displaystyle n\) pozitív egészre
\(\displaystyle \sum_{\substack{i_0,i_1,\ldots,i_K\ge0 \\ i_0+i_1+\ldots+i_K=n}} \frac{a_{i_1}\cdot\ldots\cdot a_{i_K}}{i_0+1} =0. \)
Mutassuk meg, hogy \(\displaystyle n\ge1\) esetén \(\displaystyle a_n>0\).
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)