KöMaL Problems in Mathematics, September 2016
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 10, 2016. |
K. 505. A certain job was completed by three workers. They manufactured machine parts (each machine part was made by one particular worker). The whole task took 15 hours, and the total wages paid to the three of them were \(\displaystyle 142\;000\) forints (HUF, Hungarian currency). The wages were proportional to the quantity of machine pars manufactured. It took the first worker 12 minutes to make one machine component. The second worker got twice as much money as the first worker, and the third one was paid \(\displaystyle 8\;000\) forints less than the second one. How many machine components did each of the three workers make?
(6 pont)
solution (in Hungarian), statistics
K. 506. Out of the set of integers from 1 to 1000, remove all multiples of 2. Then remove all multiples of 3 from the remaining set of numbers. Then continue to remove the multiples of 5, 7, 11, 13, 15, 17, up to 19. At the end of this procedure, select all composite numbers remaining, and add them together. What is the total obtained?
(6 pont)
solution (in Hungarian), statistics
K. 507. A six-pointed star is inscribed in each of two congruent regular hexagons. A smaller six-pointed star is then inscribed in the smaller hexagon formed inside the first star. The points of the star are the vertices of the corresponding hexagon in one case, and the midpoints of the sides of the hexagon in the other case. The resulting figures are shown in the diagram.
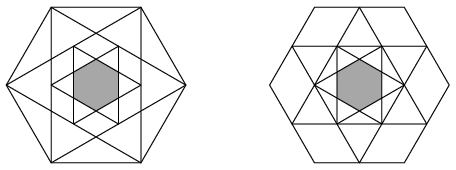
Compare the areas of the two small shaded hexagons.
(6 pont)
solution (in Hungarian), statistics
K. 508. Earthquakes are getting more and more frequent in Wonderland. Several houses have developed cracks in the walls, some even fell down. The council of elders decided to reform building regulations. They became convinced that the condition for a brick wall being earthquake-proof is that no vertical or horizontal line should extend through it completely along the sides of the bricks. The dimensions of the bricks are \(\displaystyle 1 \times 2\).
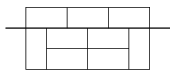
The wall in the figure is wrong, since there is a horizontal line cutting all through it
\(\displaystyle a)\) Design a plan for a \(\displaystyle 6 \times 8\) earthquake-proof wall, and another one for a \(\displaystyle 8 \times 8\) earthquake-proof wall.
\(\displaystyle b)\) Prove that it is impossible to build a \(\displaystyle 6 \times 6\) earthquake-proof wall.
(6 pont)
solution (in Hungarian), statistics
K. 509. Nine friends decided to form clubs. Each club will have three members, and any two clubs may have at most one member in common. What is the greatest possible number of clubs they can form?
(6 pont)
solution (in Hungarian), statistics
K. 510. The numbers \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) are not necessarily different real numbers. Given that \(\displaystyle ab=c\), \(\displaystyle bc=a\) and \(\displaystyle ca=b\), find all possible values of \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\).
(6 pont)
 |
Problems with sign 'C'Deadline expired on October 10, 2016. |
C. 1364. The citizens of a village were having a vote to elect a mayor. There were two candidates: Charlie and Alex. Participation was remarkable, 90% of the population eligible to vote took part. 128 votes turned out to be invalid. Charlie received 248 more valid votes than Alex. 49% of the whole population eligible to vote voted for Charlie. How many votes did he get?
(German competition problem)
(5 pont)
solution (in Hungarian), statistics
C. 1365. A square is drawn over each side of a regular \(\displaystyle n\)-gon, on the outside. The outer vertices of the squares form a regular polygon of \(\displaystyle 2n\) sides. How many sides did the original polygon have?
(5 pont)
solution (in Hungarian), statistics
C. 1366. The creatures living on asteroid GZs4-26 count in base three. The digits they use are \(\displaystyle \triangle\), \(\displaystyle \square\) and \(\displaystyle \bigcirc\), in some order. Given that \(\displaystyle \square\square\square\cdot \triangle\triangle =\square\bigcirc \triangle\square\triangle\), determine the result of the multiplication \(\displaystyle \triangle\square\bigcirc\cdot \square\bigcirc\square\triangle\).
(5 pont)
solution (in Hungarian), statistics
C. 1367. The convex octagon \(\displaystyle ABCDEFGH\) has a centre of symmetry. Prove that the sum of the areas of the quadrilaterals \(\displaystyle ABEF\), \(\displaystyle BCFG\), \(\displaystyle CDGH\) and \(\displaystyle DEHA\) is twice the area of the octagon.
(5 pont)
solution (in Hungarian), statistics
C. 1368. Solve the equation
\(\displaystyle {[x]}^2+ {\{x\}}^2 + x^2 +2[x]\{x\}=4x-2x[x]-2x\{x\}-1, \)
where \(\displaystyle [x]\) denotes the greatest integer not greater than the number \(\displaystyle x\), and \(\displaystyle \{x\}\) denotes the difference between \(\displaystyle x\) and \(\displaystyle [x]\).
(5 pont)
solution (in Hungarian), statistics
C. 1369. The coordinates of the centroid of a triangle are \(\displaystyle \left(5;-\frac{5}{3}\right)\), its orthocentre is \(\displaystyle (3;-1)\), and one vertex is \(\displaystyle (7;3)\). Find the coordinates of the other two vertices.
(5 pont)
solution (in Hungarian), statistics
C. 1370. In the school cafeteria, nine students sit down to three vacant tables with four seats around each. What is the probability that there is a different number of students sitting at each table?
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 10, 2016. |
B. 4804. With his sword received from the queen of the lakes, Sir Robin wants to free the town of Agnor from a dragon. The dragon has three heads and three tails. With one slash, he may cut off one head, two heads, one tail or two tails. If he cuts off one head, the dragon will immediately grow three heads in its place. If he cuts off two heads, then nothing will grow in its place. If he cuts off one tail, there will be two tails growing immediately. Finally, if he cuts off two tails then the dragon will grow a head. What is the minimum number of cuts needed to kill the dragon (that is, in order that the dragon has no heads or tails remaining at all)?
(German competition problem)
(3 pont)
solution (in Hungarian), statistics
B. 4805. Solve the simultaneous equations \(\displaystyle x+y+z=2\), \(\displaystyle xyz=2(xy+yz+zx)\) on the set of real numbers.
Proposed by J. Szoldatics, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4806. Given a circular disc \(\displaystyle K\) and two points on it, separated by a distance larger than \(\displaystyle 2\) units. Show that \(\displaystyle K\) contains a disc of unit radius that does not contain either of the two points.
Proposed by Gy. Károlyi, Budajenő
(3 pont)
solution (in Hungarian), statistics
B. 4807. A square is drawn over each side of a right-angled triangle \(\displaystyle ABC\) of unit area, on the outside. Denote the centres of the squares by \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\). Prove that the area of triangle \(\displaystyle DEF\) is at least two.
(Kvant)
(4 pont)
solution (in Hungarian), statistics
B. 4808. A point \(\displaystyle (a;b)\) of the coordinate plane, where \(\displaystyle a\) and \(\displaystyle b\) are positive integers, is coloured red. Then if a point \(\displaystyle (x;y)\) is red then point \(\displaystyle (x+1;y+1)\), as well as point \(\displaystyle \left(\frac x2;\frac y2\right)\) are also coloured red, provided that \(\displaystyle x\) and \(\displaystyle y\) are both even. If \(\displaystyle (x;y)\) and \(\displaystyle (y;z)\) have both been coloured, then we will also colour the point \(\displaystyle (x;z)\) red. What is the distance from the origin to the closest point coloured red?
Proposed by Z. Bereczki, Szeged
(5 pont)
solution (in Hungarian), statistics
B. 4809. Rose colours every point of the number line either blue or red. Violet will perceive a point as purple if however small a neighbourhood of the point is considered, there exist both a red point and a blue point in it. Is it possible that the numbers Violet sees purple
\(\displaystyle a)\) cover the whole number line,
\(\displaystyle b)\) are exactly the integers,
\(\displaystyle c)\) are exactly the rational numbers?
Proposed by B. Maga, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4810. Two angles of triangle \(\displaystyle ABC\) are \(\displaystyle BAC\sphericalangle=15^{\circ}\) and \(\displaystyle ABC\sphericalangle=30^{\circ}\). The perpendicular drawn to side \(\displaystyle AC\) at point \(\displaystyle C\) intersects line segment \(\displaystyle AB\) at \(\displaystyle D\), and the perpendicular bisector of \(\displaystyle AB\) intersects line \(\displaystyle CD\) at \(\displaystyle E\). Extend line segment \(\displaystyle AB\) beyond \(\displaystyle B\) by the length of line segment \(\displaystyle BC\) to get \(\displaystyle G\). Prove that the points \(\displaystyle B\), \(\displaystyle G\), \(\displaystyle E\), \(\displaystyle C\) lie on a circle of diameter \(\displaystyle \sqrt{2} \cdot AB\).
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
B. 4811. Prove that
\(\displaystyle \frac1{a_1} + \frac1{[a_1,a_2]} + \frac1{[a_1,a_2,a_3]} + \ldots + \frac1{[a_1,a_2,\ldots,a_n]} < 2, \)
for all integers \(\displaystyle 0<a_1<a_2<\ldots<a_n\), where the symbol \(\displaystyle [\dots]\) stands for the least common multiple.
(6 pont)
solution (in Hungarian), statistics
B. 4812. Let \(\displaystyle C_1\), \(\displaystyle A_1\) and \(\displaystyle B_1\) denote the feet of the altitudes drawn to sides \(\displaystyle AB\), \(\displaystyle BC\) and \(\displaystyle CA\) of an acute-angled triangle \(\displaystyle ABC\), respectively. The perpendicular projections of the orthocentre of triangle \(\displaystyle ABC\) on the lines \(\displaystyle A_1B_1\), \(\displaystyle B_1C_1\), \(\displaystyle C_1A_1\) are \(\displaystyle C_2\), \(\displaystyle A_2\) and \(\displaystyle B_2\), respectively. Prove that the lines \(\displaystyle AA_2\), \(\displaystyle BB_2\) and \(\displaystyle CC_2\) are concurrent, and their intersection lies on the Euler line of triangle \(\displaystyle ABC\).
Proposed by Sz. Miklós, Herceghalom
(6 pont)
 |
Problems with sign 'A'Deadline expired on October 10, 2016. |
A. 674. Let \(\displaystyle a_1, \ldots, a_n>1\) be integers satisfying the inequality
\(\displaystyle \sum_{i=1}^{n} \frac{1}{a_{i}+1} \le \frac{7}{12}. \)
Every year, the government of Optimistica publishes its Annual Report with \(\displaystyle n\) economic indicators. For each \(\displaystyle i=1,\ldots,n\), the possible values of the \(\displaystyle i\)-th indicator are \(\displaystyle 1, 2, \ldots, a_i\). The Annual Report is said to be optimistic if at least \(\displaystyle n - 1\) indicators have higher values than in the previous report. Prove that the government can publish optimistic Annual Reports in an infinitely long sequence.
Based on the problem of the 1st International Olympiad of Metropolises
(5 pont)
solution (in Hungarian), statistics
A. 675. Let \(\displaystyle r(x)\) be a polynomial with real coefficients whose degree \(\displaystyle n\) is odd. Prove that the number of pairs of polynomials \(\displaystyle p(x)\) and \(\displaystyle q(x)\) with real coefficients satisfying the equation \(\displaystyle \big(p(x)\big)^3 + q(x^2) = r(x)\), is smaller than \(\displaystyle 2^n\).
Based on the problem of the 1st International Olympiad of Metropolises
(5 pont)
A. 676. Let \(\displaystyle \mathcal{K}\) be a circle with diameter \(\displaystyle OI\). Construct a one-to-one correspondence \(\displaystyle f \colon \mathcal{K}\setminus \{O,I\}\to\mathbb{R}\setminus\{0\}\) with the following property: for every four distinct points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) of \(\displaystyle \mathcal{K}\), other than \(\displaystyle O\) and \(\displaystyle I\), \(\displaystyle f(A)f(B)=f(C)f(D)\) is satisfied if and only if the lines \(\displaystyle AB\), \(\displaystyle CD\) and \(\displaystyle OI\) are concurrent or parallel to each other.
(5 pont)
Upload your solutions above.
