A KöMaL 2017. februári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2017. március 10-én LEJÁRT. |
I. 421. Az első világháborúban fontossá vált a rádión küldött üzenetek rejtjelezése, hogy azokat az ellenség – lehallgatás esetén – ne tudja megfejteni. A háború egyik leghíresebb titkosítási rendszere az ADFGVX kódolás volt, amit a németek vezettek be, és 1918. március 5-én kezdtek el alkalmazni. Egy francia hadnagy, Georges Painvin azonban viszonylag hamar, már június 2-án megfejtett egy ezzel a kóddal rejtjelezett üzenetet.
A rejtjelezésnél használt kulcs két részből áll: egy 6×6-os kódtáblából, amely tartalmazza a 26 nagybetűt és a 10 számjegyet, valamint egy kódszóból.
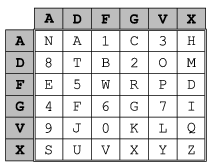
A kódtábla első sorát és első oszlopát kiegészítik az A, D, F, G, V, X karakterekkel, ezek lesznek a sor-, illetve az oszlopazonosítók. (Azért ezeket a karaktereket választották, mert az akkoriban használt, nekik megfelelő Morse jelek jól elkülöníthetőek voltak.)
A példánkban használt táblázat az ábrán látható, a kódszó legyen KOMAL, a nyílt szöveg pedig legyen: AZAKCIO7KORINDUL.
Maga a rejtjelezés több lépésből áll:
1. Meghatározzuk a kódtábla alapján a nyílt szöveg karaktereinek koordinátáit (sor, oszlop), és azokat egymás mellé írjuk:

2. A kódszó karakterei alá sorfolytonosan beírjuk az így kapott koordinátasorozatot. Példánkban ezt az első táblázat mutatja.

3. Átrendezzük a táblázat oszlopait úgy, hogy a kódszó betűi névsorba kerüljenek. Az átrendezés utáni állapotot példánkban a második táblázat szemlélteti.
4. A titkos üzenetet úgy kapjuk meg, hogy a második (kódszó nélküli) táblázatot ,,oszlopfolytonossá'' alakítjuk. Példánkban:
XAVDXXADGVFAVAGGVADXGDGGXDVXVGFV
Készítsünk programot i421 néven, amely lehetővé teszi egy megadott szöveg rejtjelezését és visszafejtését a fenti leírás alapján. A program első parancssori argumentuma egy karakter, amely megadja, hogy a felhasználó az adatokat rejtjelezni vagy visszafejteni szeretné (R/V), második a kódot tartalmazó fájl neve, a harmadik a rejtjelezendő/visszafejtendő adatokat tartalmazó fájl neve, a negyedik pedig a kimeneti fájl neve legyen. A kódot tartalmazó fájl első hat sora a kódtábla sorait tartalmazza (szóközök és a koordináták nélkül), utolsó sora pedig a kódszót.
Feltételezhetjük, hogy a bemeneti adatok csak az angol ábécé fentieknek megfelelő nagybetűit tartalmazzák. Feltehetjük továbbá, hogy a rejtjelezendő/visszafejtendő állomány mérete legfeljebb 1000 karakterből áll, továbbá a kódszó nem hosszabb 10 karakternél.
Beküldendő egy i421.zip tömörített állományban a program forráskódja és dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
Letölthető fájlok (egy lehetséges kód, valamint egy lehetséges rejtjelezendő fájl): be.txt , kod.txt .
(10 pont)
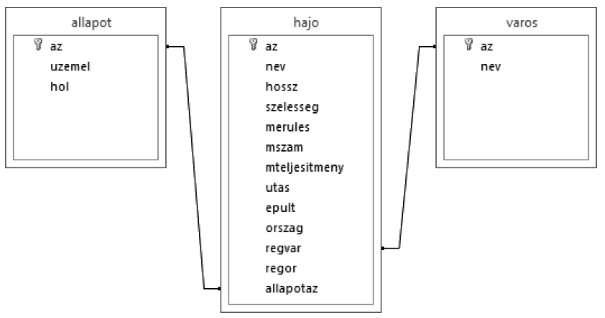
I. 422. A http://folyamhajo.hu folyamhajózási információs portálról minden olyan folyami kabinos személyhajóról (szállodahajó) jellemző adatokat ismerhetünk meg, mely az elmúlt évtizedekben legalább egyszer megfordult hazánkban. Az adatok a hajo.txt, a varos.txt és az allapot.txt állományokban állnak rendelkezésünkre. Az állományok tabulátorral tagolt, UTF-8 kódolású szövegfájlok, az első sorok a mezőneveket tartalmazzák.
1. Készítsünk új adatbázist regiszter néven. A mellékelt adatállományokat importáljuk az adatbázisba a fájlnévvel azonos hajo.txt, varos.txt és allapot.txt néven. Beolvasáskor állítsuk be a megfelelő adatformátumokat és kulcsokat. A táblákba ne vegyünk fel új mezőt.
Táblák

Készítsük el a következő feladatok megoldásait. Az egyes lekérdezéseknél ügyeljünk arra, hogy mindig csak a kért értékek jelenjenek meg és más adatok ne. Megoldásainkat a zárójelben lévő néven mentsük el.
2. Készítsünk lekérdezést, amely ábécérendben jeleníti meg a jelenleg is üzemelő személyhajók nevét. (2szemely)
3. Készítsünk lekérdezést, amely kilistázza a Viking Hajókirándulásnak, a dunai turisztikai célú hajózás meghatározó szereplőjének hajóit. Ezeknek a hajóknak a neve a ,,Viking'' szórészletet tartalmazza. (3viking)
4. Testvérhajónak nevezik azokat a hajókat, amelyeket ugyanabban az évben és országban gyártottak, valamint hosszúságuk, szélességük és merülésük is megegyezik. Soroljuk fel lekérdezés segítségével a ,,VIKING NEPTUNE'' testvérhajóit. (4neptune)
5. Lekérdezés segítségével adjuk meg, hogy melyik három európai városban regisztrálták a legtöbb hajót. (5kozpont)
6. Lekérdezés segítségével soroljuk fel azoknak az országoknak a betűjelét, ahol hajóregisztráció történt, de hajóépítő országként egy hajónál sincsenek megjelölve. (6konyveles)
7. Adjuk meg lekérdezés segítségével annak a hajónak, vagy hajóknak a nevét, amelynél teljes kihasználtság esetén a legnagyobb az egy utasra eső maximális teljesítmény. A teljes teljesítményt a motorszám és a névleges motorteljesítmény szorzataként számoljuk. (7eros)
8. Lekérdezés segítségével számoljuk meg, hogy az adatbázisban hány olyan hajó van, amelynek a maximális utasszáma az 50–99, a 100–149, a 150–199, illetve a 200–249 tartományokban van. (8kategoriak)
Beküldendő egy tömörített i422.zip állományban az adatbázis, valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott adatbázis-kezelő neve és verziószáma.
Letölthető állományok: allapot.txt , hajo.txt , varos.txt .
(10 pont)
I. 423. Ha egy m tömegű pontszerű testet egy D rugóállandójú rugóra függesztünk, majd egyensúlyi helyzetéből függőlegesen kitérítjük, akkor a test harmonikus rezgőmozgást végez. A mozgással az I. 417. feladatban foglalkoztunk. A feladatot általánosítjuk, és most azt vizsgáljuk, hogy milyen mozgás alakul ki akkor, ha a kitérés kezdetben nem függőleges.
A test mozgásának leírása igen összetett, a részletek iránt érdeklődőknek ajánljuk a Fizikai Szemle 2006/10. számát: http://fiztan.phd.elte.hu/nyilt/publokt/Tel-200610.pdf. A pontszerű test mozgásegyenletének megoldása helyett alkalmazzunk szimulációt a mozgás leírására.
Legyen egy D rugóállandójú húzó-nyomó rugó, amely a kezdeti l0 hosszúságtól való Δl megnyúlással vagy összenyomással ellentétes irányú, és azzal arányos Frugó=−D⋅Δl erőt fejt ki. Az elhanyagolható tömegű rugó egyik vége egy pontban rögzített (e körül szabadon elfordulhat), másik végén egy m tömegű test található. Könnyen látható, hogy ha a testet egy pontban kezdősebesség nélkül elengedjük, akkor egy olyan függőleges síkban mozog, amely a rugó rögzítési pontját és a test kezdőpontját is tartalmazza. Feladatunk az, hogy ennek a síkmozgásnak a pályáját megrajzoljuk.
A szimulációt a következő leírás alapján végezzük:
1. Vonatkoztatási rendszerként célszerű olyan derékszögű koordináta-rendszert használni, amelynek y tengelye függőleges, origója pedig a rugó felfüggesztési pontja.
2. Kezdetben (és minden későbbi pillanatban) ismerjük a test r(x,y) helyvektorát, amiből kiszámítható a nyújtatlanul l0 hosszúságú rugó aktuális hossza és Δl megnyúlása vagy összenyomódása.
3. A rugóerő nagyságát a Frugó=−D⋅Δl képletből kapjuk, az erő irányát a test helyzetéből tudjuk meghatározni.
4. A testre a rugón kívül még a nehézségi erő hat. Az erőhatások függetlenségének elve alapján mindkét erőt felbonthatjuk a koordináta-rendszer tengelyeinek megfelelően, így ki tudjuk számítani az összegüket, tehát a testre ható eredő erő koordinátáit.
5. Ezek alapján megkapható a test a pillanatnyi gyorsulásvektora, illetve annak koordinátái.
6. A test az adott helyzetéből Δt idő alatt elmozdul. A Δr elmozdulásvektort közelítsük a pillanatnyi sebesség és gyorsulás értékeiből a
Δr=v⋅Δt+12a⋅(Δt)2
képlet segítségével.
7. A test pillanatnyi v sebességét Δt idővel később a v(Δt)=v+a⋅Δt kifejezéssel adjuk meg.
8. Helyezzük tehát a testet az új helyére, végezzük el a rajzolást, majd folytassuk a szimulációt a 2. ponttól.
A program legyen felhasználóbarát, tehát oldjuk meg, hogy a fizikai paramétereket (m, D, l0, Δt) és a test r(x,y) kezdeti pozícióját a szimuláció megkezdése előtt a felhasználó megadhassa.
Beküldendő egy i423.zip tömörített mappában a szimulációt végző program forráskódja, a fordításhoz és futtatáshoz szükséges környezet leírása. A megoldáshoz a versenykiírásban szereplő fejlesztői rendszerek egyike, illetve ahhoz egyszerűen telepíthető ingyenes grafikus kiegészítő könyvtár (pl. SFML) használható.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2017. március 10-én LEJÁRT. |
I/S. 15. Benedek ásatásokon segédkezik, ahol az egyik nap találtak egy olyan szöveges dokumentumot, amelyben csak A és B betűkből álló, meglehetősen hosszú szavak szerepeltek. Benedek azt a feladatot kapta a főnökétől, hogy a szavak felett ívekkel, kettesével kösse össze az azonos betűpárokat (az A-t az A-val, a B-t a B-vel), majd számolja meg a dokumentumban szereplő ,,szép'' és ,,nagyon szép'' szavakat. ,,Szép''-nek nevezzük azokat a szavakat, amelyekben kialakítható olyan párosítás, amelynél minden egyes betűnek van párja és a rajzolt ívek nem keresztezik egymást. ,,Nagyon szép''-ek azok a szavak, amelyekben a szép kritériumnak megfelelő összekötés egyértelmű, vagyis pontosan egyféle a kereszteződés nélküli megfelelő összeköttetés.
A feladatunk a szövegben előforduló ,,szép'' és ,,nagyon szép'' szavak megszámolása.
A standard bemenet első sora a dokumentumon szereplő szavak N (1≤N≤1000) számát, a következő N sor pedig a csupa A és B betűből álló szavakat tartalmazza. Egy-egy szó hossza legalább 1 és legfeljebb 100000 betű. Az összes szó hosszának összege nem nagyobb, mint 1000000. A standard kimenet első sorába a ,,szép'' szavak számát, míg a második sorába a ,,nagyon szép'' szavak számát kell írni.
Pontozás: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. További 7 pontot ér a ,,szép'' szavak számának helyes megadása, és további 2 pont a ,,nagyon szép'' szavak helyes megszámlálására jár.
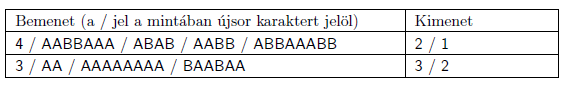
Magyarázat:
AABBAAA – nem szép és nem nagyon szép, mivel nincs minden betűnek párja;
ABAB – nem szép és nem nagyon szép, a betűk feletti párosítás metszi egymást;
AABB – szép és nagyon szép – az összekötés egyértelmű;
ABBAAABB – szép, de nem nagyon szép, mert az első A-t a 2. és a 4. A-val is lehet kötni, így többféleképpen is létrejöhet az átmetszés nélküli párosítás.
Beküldendő egy tömörített is15.zip állományban a program forráskódja és rövid dokumentációja, amely ismerteti a megoldás menetét és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2017. március 10-én LEJÁRT. |
S. 114. A vulkanikus eredetű szigetek gyakran egy vonal mentén helyezkednek el. Egy ilyen szigetcsoport mesés kincset rejt. Kalóz vagy, és hozzájutottál egy térképhez, amelyen az összes sziget rajta van. Mindegyik szigeten van valamennyi kincs, melyeknek a pontos helyét és értékét minden sziget esetén ismered. Legénységet toboroztál és készen állsz a nagy útra, viszont a térkép alapján elkezdtél kételkedni, hogy talán nem minden egyes szigetre érdemes elhajózni, ugyanis a hajózás nagyon megdrágult az utóbbi hónapokban.
Minden sziget esetében ismered, hogy mennyibe kerül odahajózni a kiindulási kikötőből (most itt vagy, ez a szigetcsoporton kívül helyezkedik el), illetve minden pár szomszédos szigetre tudod, hogy mennyibe kerül az út a két sziget között (mindkét irányban ugyanannyi). A kiindulási kikötőből el kell hajóznod az egyik szigetre, ezután a szigetek között tetszőlegesen hajózhatsz. Ezenkívül néhányan megtudták, hogy nálad van a kincses térkép, így irigyek és tudod, hogy bármire képesek lennének, hogy megszerezzék, ezért soha többé nem jöhetsz vissza a kiindulási kikötőbe (vagyis a szigetcsoporton belül akárhol befejezheted az utadat). Ez azt is jelenti, hogy akkor is el kell hajóznod, ha a kincskereső utad veszteséges lenne, ekkor a legkisebb veszteségre kell törekedned. Készíts programot, amely megadja, hogy hogyan hajózz, hogy a legtöbb nyereségre, vagy a legkisebb veszteségre tegyél szert.
A standard bemenet első sorában a szigetek N száma van. A második sor N darab nemnegatív egész számot tartalmaz, az i-edik K[i], az i-edik szigeten lévő kincs értéke. A harmadik sor szintén N darab nemnegatív egész számot tartalmaz, az i-edik H[i], a kiindulási kikötőből az i-edik szigetre hajózás költsége. A negyedik sor N−1 darab nemnegatív egész számot tartalmaz, az i-edik szám S[i], az i-edik és az (i+1)-edik sziget közötti hajózás költsége.
A standard kimenet első sorába írd ki a maximális hasznot/minimális veszteséget, a második sor tartalmazzon egy maximális hasznot/minimális veszteséget hozó útvonalat: az első szám legyen L, a hajóutak (egy-egy hajóút a kiindulási kikötőből egy szigetre hajózás, valamint a hajóutak száma), ezt kövesse L sziget sorszáma, a hajóutak célpontjai.
Pontozás: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. 4 pontot ér a maximális haszon/minimális veszteség helyes meghatározása, és további 5 pontot ér a szigetek egy lehetséges, a fenti eredményt adó bejárása. Ha a haszon/veszteség értéke helytelen, akkor a hajóutakért nem jár pont.
Korlátok: 1≤N≤200000, 0≤K[i],H[i],S[i]≤109.

Magyarázat: Az ötödik szigetre hajózunk először (1 kincs – 5 költség), majd sorban jön a 4-es, 3-as, majd a 2-es (rendre 12+15+10 kincs – 15+1+3 költség) összesen 38−24=14 haszon.
Beküldendő egy tömörített s114.zip állományban a program forráskódja és rövid dokumentációja, amely ismerteti a megoldás menetét és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.
|
|

