A KöMaL 2018. novemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2018. december 10-én LEJÁRT. |
I. 466. A mérgezett csoki egy nagyon egyszerűen leírható kétszemélyes játék. A játékosok felváltva ,,törnek'' a táblából és az veszít, akinek a végén csak a mérgezett kocka marad. Ismert, hogy a kezdőnek van nyerő stratégiája, de az csak az N×N és a 2×N méretű tábla esetén fogalmazható meg egyszerűen, más méretű táblát használva a játék valós izgalmat hordoz.
A játékról bővebben például a http://web.cs.elte.hu/szakdolg/ghorvath.pdf címen elérhető diplomamunkában olvashatunk.
Ebben a feladatban a következő formában játszunk:
∙ a csokoládétábla N sorból és M oszlopból áll;
∙ az egyes csokoládékockákat két egész számmal azonosítjuk;
∙ a mérgezett csokoládékocka az (M,N) számpárral adható meg;
∙ a táblából minden lépésben legalább egy kockát törünk le. A törést minden esetben a teljes csokoládétábla (1,1) sarkával ,,szemközti'' (i,j) számpárral adjuk meg. Ekkor minden, még meglévő (x,y) csokoládékockát elveszünk, amelyre x≤i és y≤j.
A játékosok dokumentálni szerették volna a játékot, ezért a soron következő lépést egy kártyalapra írták, majd a másik játékos előző lépését tartalmazó lapra helyezték. Ez a módszer sajnos nem volt jó, mert egy ajtónyitáskor keletkező huzat a kártyákat lesodorta az asztalról és azok összekeveredtek. Készítsünk programot, amely a kártyákat egy lehetséges törési sorrendbe állítja és megadja, hogy a meghatározott sorrend esetén az egyes versenyzőkhöz hány csokoládékocka került.
A program standard bemenetének első sorában a csokoládétábla mérete, az oszlopok és a sorok száma, azaz M és N, valamint a kártyalapok K száma található. A következő K sorban az egyes kártyákon szereplő oszlop, sor értékpárok szerepelnek. A kimenet első sorában K egész szám szerepel: a töréseket leíró kártyák egy lehetséges sorrendje. A második sorban ezen sorrend esetén az első, illetve a második játékos által letört kockák száma. Az elválasztó karakter minden esetben a szóköz. A bemenetben egyetlen szám értéke sem nagyobb 1000-nél.

Beküldendő egy i466.zip tömörített állományban a program forráskódja és a működéséhez szükséges egyéb fájlok, továbbá a hozzá kapcsolódó dokumentáció. Utóbbi világítson rá a problémamegoldás lényeges elemeire, valamint tartalmazza, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 467. (É). Idézet a Wikipédiáról: ,,A Steam egy tartalomtovábbító és -kezelő rendszer, amelyet a Valve Software fejlesztett ki. Funkciói különféle számítógépes szoftverek (túlnyomórészt játékok) digitális áruházi rendszerben történő értékesítése, többjátékos módok menedzselése, és közösségépítő háló fenntartása ldots 2015-ben a Steam-en eladott, illetve itt érvényesített termékek értéke meghaladta a három és fél milliárd dollárt, ldots több mint 125 millió felhasználója van. (https://hu.wikipedia.org/wiki/Steam.)
Feladatunk a Steam-en elérhető toplistás játékok adatainak feldolgozása adatbázis-kezelő program segítségével. Forrás: http://steamcharts.com/top (utolsó letöltés 2018. 01. 07.).
1. Készítsünk új adatbázist steam néven. A letölthető adatállományokat importáljuk az adatbázisba a fájlnévvel azonos nevű táblákba. Beolvasáskor állítsuk be a megfelelő típusokat és kulcsokat. Az állományok tabulátorral tagolt, UTF-8 kódolású szövegfájlok, az első sorok a mezőneveket tartalmazzák.
2. Amelyik feladat megoldásához szükségünk van rá, alakítsunk ki megfelelő kapcsolatokat a táblák között.
Táblák:


Készítsük el a következő feladatok megoldását. Az egyes lekérdezéseknél ügyeljünk arra, hogy mindig csak a kért értékek jelenjenek meg és más adatok ne. Megoldásainkat a zárójelben lévő néven mentsük el.
3. Melyik napon játszottak több órát a Steam-en: szenteste, vagy újév napján? Jelenítsük meg a dátumot. (3csucsnap)
4. Az ingyenes játékok közül melyiknek van a legtöbb értékelése? Írassuk ki a játék nevét. (4ingyenertek)
5. Hány esetben nincsen megadva a javasolt grafikus kártya típusa, ha egyébként az adott operációs rendszer verzió támogatott? (5hiany)
6. Mennyibe kerülne megvásárolni azokat a fizetős játékokat, amelyeknek több, mint 150000 értékelése van és azok nagyon pozitívak? Az eredményt euróban jelenítsük meg, tizedes helyek nélkül. (6ara)
7. Vizsgáljuk meg, hogy hány Multiplayer játék érhető el Windows, és hány MacOS operációs rendszerre. (7multi)
8. Készítsünk lekérdezést, ami összehasonlítja, hogy átlagosan hány GB szabad helyet igényelnek azok a MacOS operációs rendszer alatt futtatott játékok, melyekhez szükséges szélessávú internetkapcsolat, és amelyekhez nem. (8osszehasonlitas)
9. Készítsünk jelentést, ami szemlélteti, hogy a ,,Dota 2'' játékkal hány órát játszottak decemberben az egyes napokon. A jelentésben az óraszám szerint csökkenő sorrendben jelenjenek meg az értékek és a hozzá tartozó napok. A jelentés címe legyen Dota 2 – december. (9dota)
10. Összesen hány nyelven érhetőek el az egyes játékok felületei? Jelenítsük meg a játék nevét, és a nyelvek számát. (10nyelv)
Beküldendő egy tömörített i467.zip állományban az adatbázis, valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott adatbázis-kezelő neve és verziószáma.
Letölthető állomány: steam.zip.
(10 pont)
I. 468. A Mastermind játék már korábban is előkerült az informatika feladatok között. Most ennek a számjegyes változata szerepel feladatunkban: kitalálandó négy számjegy, amelyek akár egyformák is lehetnek. A játékot egy számítógép ellen játssza az általunk írt program. A számítógép ,,gondol'' négy számra, majd programunk minden lépésben négy számot tippel, válaszként pedig megkapja, hogy hány számjegy van jó helyen és mennyi szerepel még a tippünkből a gondolt számok között rossz helyen. (https://hu.wikipedia.org/wiki/Mastermind#Számjegyesváltozat.)
Az ellenféllel az alábbi formában kommunikálhatunk a kezdés, kérdés és rákérdezés parancsokkal.
| művelet | url | válasz |
| kezdés | http://localhost/mm/ellenfel.php?muvelet=kezdes | OK |
| kérdés | http://localhost/mm/ellenfel.php?muvelet=kerdes&ertek=1234 | 2 1 |
| kérdés | http://localhost/mm/ellenfel.php?muvelet=kerdes&ertek=1245 | 0 2 |
| rákérdezés | http://localhost/mm/ellenfel.php?muvelet=rakerdezes&ertek=5334 | 4 0 |
A táblázat válasz oszlopában a kérdésnél és a rákérdezésnél a számok között pontosan egy szóköz van. Nem cél, hogy a lehető legkevesebb lépésben jussunk megoldásra, de törekedjünk arra, hogy olyan kérdést ne tegyünk fel, amely ellentmondásban van a korábban kapott válaszokkal.
A feladat megoldásaként a versenykiírásban szereplő eszközökkel elkészíthető alkalmazások mellett más programozási eszközöket, akár webes alkalmazásokat is elfogadunk. Feltétel, hogy a program indítását követően a rákérdezéssel bezárólag ne legyen szükség felhasználói beavatkozásra és a futás során ne igényeljen aktív netkapcsolatot.
Beküldendő egy i468.zip tömörített állományban a program forráskódja és a működéséhez szükséges egyéb fájlok, továbbá a hozzá kapcsolódó dokumentáció. Utóbbi a problémamegoldás lényeges elemeire világít rá, valamint tartalmazza, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
Értékelés: 4 pont jár, ha a program szabályos eszközökkel kitalálja a megoldást, további 4 pontot ér, ha a kérdések nincsenek ellentmondásban a korábban kapott válaszokkal. A körültekintően elkészített dokumentáció 2 pontot ér.
A kommunikációra példát adó ellenfel.php fájl letöltése: ellenfel.zip
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2018. december 10-én LEJÁRT. |
I/S. 30. Matekórán Bence és osztálytársai az összeadást, szorzást és a négyzetre emelést gyakorolják a következő módon: A tanár felír a táblára egy N×M-es táblázatba számokat, ezután felad Q számolási feladatot a diákoknak. Egy-egy feladatban kiválasztja egy tetszőleges A×B téglalap alakú részét a táblázatnak, majd megkéri a diákokat, hogy az ott levő számok mindegyikét szorozzák meg a-val és az eredményhez adjanak hozzá b-t, majd minden így kapott számot emeljenek négyzetre, végül adják össze őket. Az így kapott összeg kiszámítását jelenti egy-egy feladat.
Bence lázadó típus, ezért a végén csak a páros számokat adja össze. Adjuk meg mind a Q feladatra, hogy milyen eredményt kapott Bence. Egy feladat elvégzése után a táblázat változatlan marad, tehát mindegyik feladatnál az eredeti táblázat számaival kell dolgozni, de természetesen más a és b értékekkel, illetve más-más táblázatrészben.
Bemenet: az első sor tartalmazza a táblázat sorainak N, oszlopainak M számát és a kérdések Q számát. A sorok fentről lefelé 0-tól (N−1)-ig vannak indexelve, az oszlopok balról jobbra 0-tól (M−1)-ig. A következő N sor M számot tartalmaz: a táblázat számait fentről lefelé és balról jobbra. A következő Q sor mindegyike hat számot tartalmaz: az a, b, n1, m1, n2, m2 számokat, ekkor azon a táblázatrészen kell elvégezni a műveleteket, aminek bal felső sarkának sorindexe n1, oszlopindexe m1; jobb alsó sorának sorindexe n2, oszlopindexe m2. Az itt levő számokat kell megszorozni a-val, hozzájuk adni b-t, négyzetre emelni a kapott számot, majd a párosakat összeadni.
Kimenet: Q sort tartalmazzon, az i. sor az i. feladat eredményét.
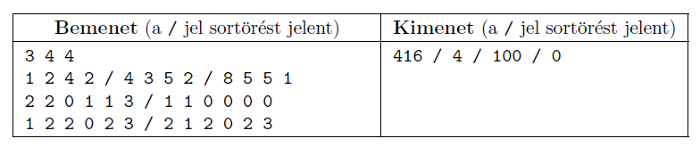
Korlátok: 1≤N,M≤1000, 1≤Q≤106, 0≤a,b és a táblázat elemei ≤100, egészek.
A pontok 20%-a kapható, ha N⋅M⋅Q≤106; további 20% kapható, ha a=1, b=0; további 20% kapható, ha b=0; további 40% kapható az eredeti bemenetre. Időlimit: 0,5 mp.
Az I/S és S-jelű feladatok megoldását a http://mester.inf.elte.hu automatikus értékelő rendszer segítségével kipróbálhatod, tesztelheted (Téma: KöMaL - 2018/19).
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2018. december 10-én LEJÁRT. |
S. 129. Egy város csatornahálózatát csomópontok és a csomópontok között levő csatornák alkotják. A városban összesen N darab csomópont van és N−1 darab csatorna, a csatornák és csomópontok egy összefüggő hálózatot alkotnak. A csomópontok különböző magasságokban vannak, a 0 indexű csomópont van a legalacsonyabban. Egy p csomópont magasabban van, mint egy r csomópont, ha a p és 0 indexű csomópontok távolsága nagyobb, mint az r és 0 indexűeké. A lejtés miatt minden csatornában egy irányban folyik a víz, a magasabban levőtől az alacsonyabban levőig. Egy csomópontból abba a csatornába folyik a víz, amelyik a vizet egy alacsonyabban levő csomóponthoz szállítja, ha van ilyen csatorna. Ha nincs, akkor a csomópontban felgyűlik a víz, nem folyik sehova. Az előbbiekből adódik, hogy kezdetben a víz mindenhonnan a 0 indexű pontba folyik, ahol az felgyűlik. Az év során csatornák dugulnak el, ilyenkor használhatatlanok, nem folyik bennük a víz. Az eldugult csatornákat lehet, hogy megtisztítják, ilyenkor újra folyik bennük a víz. Kezdetben minden csatorna tiszta.
Georgie papírcsónakokkal játszik, a csónakot elhelyezi egy p indexű csomópontban. Ekkor a papírcsónak – követve a víz folyását – végül egy r indexű csomópontban köt ki, ahol felgyűlik a víz. Segítsünk Georgienak megtalálni ezt az r csomópontot.
Bemenet: Az első sorban található a csomópontok N és a tevékenységek Q száma. A következő N−1 sorban a csomópontok indexei vannak: az i. sorban egy j szám, azt jelenti, hogy az i és j indexű pontokat csatorna köti össze, amin j felé folyik a víz. (A 0 indexűből nem folyik sehova.) A következő Q sor mindegyike egy x és egy p számot tartalmaz. Ha x=1, akkor Georgie elhelyez egy papírcsónakot a p csomópontnál. Ha x=0, akkor az a csatorna, ami p-ből szállítja a vizet eldugul, ha eddig folyt benne a víz, vagy kitisztul, ha el volt dugulva.
Kimenet: Minden papírcsónak elhelyezés után írjuk ki (szóközzel elválasztva), hogy melyik indexű csomópontba kell mennie Georgienak, hogy megtalálja a csónakját.

Korlátok: 2≤N≤105, 1≤Q≤105.
Értékelés: a pontok 20%-a kapható, ha N⋅Q≤106; további 30% kapható, ha csatorna csak eldugulhat, nem tisztulhat ki; további 50% kapható az eredeti korlátokra. Időlimit: 0,5 mp.
Az I/S és S-jelű feladatok megoldását a http://mester.inf.elte.hu automatikus értékelő rendszer segítségével kipróbálhatod, tesztelheted (Téma: KöMaL - 2018/19).
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.
|
|

