A KöMaL 2019. januári informatika feladatai

I-jelű feladatok A beküldési határidő 2019. február 11-én LEJÁRT.

I. 472. Ma már számtalan eszköz és azt vezérlő program áll rendelkezésre, hogy az igényelt méretben és formában állítsunk elő feliratokat. 40-50 évvel ezelőtt még mechanikus céleszköz volt szükséges, hogy az írógéppel írhatóhoz hasonló karaktereket nyomjunk egy vékony műanyag szalagra. A megfelelő karaktert egy tárcsa elfordításával lehetett kiválasztani, majd egy kar meghúzásával egy műanyag szalagra rögzíteni. A benyomás eredményeként a betű alakjának megfelelő kiemelkedés jött létre, egyúttal a szalag el is fehéredett. (Az eszköz ma is szerepel a boltok kínálatában.)

Az eszköz forgatható tárcsáján az ABC betűi szerepeltek. Az egyszerűbb szerkezeteknél a tárcsát csak az egyik irányban lehetett forgatni, ezért a BABA szó leírásához kétszer is körbe kell forgatni a tárcsát. Jól látható, hogy ha a tárcsa mindkét irányban szabadon forgatható lenne, sokkal gyorsabban előállna a felirat.

Készítsünk vezérlő programot egy feliratozó gép tárcsájának kezeléséhez, amely biztosítja a feliratok legrövidebb idő alatti elkészültét. A tárcsa egy karakterrel való elfordítása egy időegységet igényel. A forgásirány megváltoztatásához V időegység kell. A folyamatosan előre haladó szalag egy karakterhellyel való elmozdítása szintén egy időegység, mozgatása a tárcsa mozgatásával párhuzamosan is történhet. Az aktuális karakter benyomása is egy időegység.

A program standard bemenetének első sorában az irányváltáshoz szükséges V érték található. A második sorban pedig a felirat olvasható, amely csak az angol ábécé nagybetűit és a szóközt tartalmazhatja, legfeljebb 200 karakter hosszban. A kimenet első sorában az elkészítéshez szükséges idő, a következőben pedig a szükséges fordítások száma és az irányváltások (jele #) szerepelnek egymástól egy-egy szóközzel elválasztva.

A tárcsa az angol ábécé nagybetűit tartalmazza ábécé sorrendben. Induláskor az A karakteren áll, ha egyet fordítunk, akkor a B karakter következik.

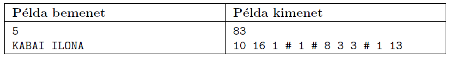
A kimenet magyarázata: A tárcsa forgatásához összesen 56 időegység kell. A forgásirány háromszori megváltoztatása 15 időegység. A 10 karakter előállítása 10 időegység. Az első szó utolsó karaktere egyezik a következő szó első karakterével, így a tárcsát nem kell forgatni, de a szalagot továbbítani kell, először a szóköz helyére, majd a második I karakter pozíciójára.

Beküldendő egy i472.zip tömörített állományban a program forráskódja és a működéséhez szükséges egyéb fájlok, továbbá a hozzá kapcsolódó dokumentáció. Utóbbi a problémamegoldás lényeges elemeire világít rá, valamint tartalmazza, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

megoldás, statisztika

I. 473. (É). Ebben a feladatban egy cég dolgozóinak adatai állnak rendelkezésünkre. A táblázat a következő adatokat tartalmazza: a dolgozó neve, neme, az a részleg, ahol a dolgozó a munkáját végzi, a céghez való belépés éve, valamint a dolgozó bére. Célunk egy olyan táblázat elkészítése, amellyel a cégvezetés elemezheti a dolgozók bérét. A feladatok megoldása során ügyeljünk arra, hogy az eredmények helyesek legyenek akkor is, ha új dolgozókat alkalmaz a cégvezetés, vagy ha egyes dolgozók időközben kilépnek.

1. Töltsük be a táblázatkezelő program egyik munkalapjára az A1 cellától kezdve a honlapunkról letölthető dolg.txt adatfájlt (tabulátorokkal tagolt, UTF-8 kódolású szövegállomány), majd mentsük a munkafüzetet dolgozok néven a program alapértelmezett formátumában.

2. Határozzuk meg az I4:I5 tartományban a cég dolgozónak számát és együttes bérét (bértömegét).

3. A cégvezetés a dolgozók bérét szeretné megemelni, a dolgozók egységesen 5% béremelést kapnak. Azok azonban, akik még így sem érik el az I2-es cellában lévő bérminimumot, a bérminimumot fogják kapni. Határozzuk meg a dolgozók új bérét az $\displaystyle F$ oszlop celláiban. Az adatokat kerekítsük egész számra.

4. Határozzuk meg az I6-os cellában, hogy hány olyan dolgozó lesz béremelés után, aki a bérminimumot kapja.

5. Írjuk be az I8-as cellába egy részleg nevét, majd határozzuk meg az I11:J12 tartomány celláiban az adott részleg dolgozóinak számát és átlagbérét nemenkénti bontásban.

6. Emeljük ki az I8-as cellában megadott részlegen dolgozók összes adatát feltételes formázással az A:F oszlopokban halványszürke háttérrel.

7. Jelenítsük meg az I14-es cellában képlettel az aktuális évet (például 2019.$\displaystyle \,$03.$\displaystyle \,$15-én 2019-et). A következő két feladatban használjuk fel ennek a cellának a tartalmát.

8. A cégvezetés szeretné külön jutalomban részesíteni a törzsgárdát, vagyis azokat a dolgozókat, akik több, mint 25 éve a cég alkalmazásában állnak. Emelje ki az ő nevüket feltételes formázással, félkövér betűstílussal.

9. A H17:I28 tartományban a dolgozók új bérének eloszlását szeretnénk meghatározni 50$\displaystyle \,$000 Ft-os sávonként. Határozzuk meg az I17:I27 tartományban képlettel, hogy hány dolgozó esik az egyes sávokba.

10. Írjuk a H30-as cellába a Maximális bért kap: szöveget, és határozzuk meg az I31-es cellába az illető nevét (felhasználhatjuk, hogy egy ilyen dolgozó van).

11. Ábrázoljuk sávdiagramon a dolgozók új bérének eloszlását! A függőleges tengelyen a sávok alsó határa jelenjen meg. A diagram címe A megemelt bér eloszlása legyen.

12. Formázzuk meg a táblázatot a mintának megfelelően.

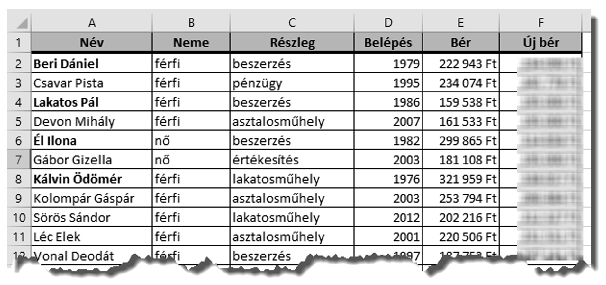
Beküldendő egy tömörített i473.zip állományban a megoldást adó táblázatkezelő munkafüzet és egy rövid dokumentáció, amely megadja a felhasznált táblázatkelő nevét és verzióját.

Letölthető fájl: dolg.txt

(10 pont)

megoldás, statisztika

I. 474. A jamaicai jégkorongbajnokság utolsó, mindent eldöntő mérkőzését a Grizzlimedvék félelmetes hírű csapata a Pingvinekkel játssza. Döntetlen esetén, vagy ha a Grizzlik győznek, ők a bajnokok. Ha viszont a Pingvinek győznek, akkor a Pingvinek nyerik a bajnokságot.

A Pingvinek – akiket alacsonyabb termetük miatt sokak esélytelenebbnek tartottak – az első két harmadban, nem kis szerencsével egygólos előnyt szereztek. A statisztikák szerint, ha a szokásos rendszerben játszanak, akkor a Grizzlik átlagosan 600, a Pingvinek átlagosan 900 másodpercenként szereznek gólt. Ha viszont a Grizzlik lehozzák a kapusukat, és öt helyett hat mezőnyjátékossal rohamoznak, akkor 180 másodpercenként szereznek, de – az üresen hagyott kapu miatt – 90 másodpercenként kapnak gólt. Ha továbbra sem változik az eredmény, mennyi idővel a mérkőzés vége előtt érdemes a Grizzliknek lehozniuk a kapusukat, hogy a lehető legnagyobb valószínűséggel kiegyenlítsenek?

Készítsünk számítógépes programot, amely megadja a választ a feltett kér­désre.

Beküldendő egy i474.zip tömörített állományban a program forráskódja és a dokumentáció, amely a megoldási módszer rövid ismertetése mellett megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

Javasolta: Kós Géza

(10 pont)

megoldás, statisztika

I/S-jelű feladatok A beküldési határidő 2019. február 11-én LEJÁRT.

I/S. 32. Egy iskola könyvtárban összesen $\displaystyle M$ darab számítógép van. Egy nap $\displaystyle N$ diák előre megadta, hogy melyik időpillanattól melyik időpillanatig szeretne használni egy gépet. Tegyük fel, hogy egy diák az $\displaystyle a_{1}$ időpillanattól a $\displaystyle b_{1}$ időpillanatig szeretne gépezni, egy másik pedig $\displaystyle a_{2}$-től $\displaystyle b_{2}$-ig. Ők csak akkor használhatják ugyanazt a gépet, hogyha $\displaystyle b_{1}<a_{2}$ vagy $\displaystyle b_{2}<a_{1}$. Ha egy diák nem tud használni egy gépet sem a teljes kért időtartam alatt, akkor a könyvtárosnak el kell utasítania a kérését. Mivel csak $\displaystyle M$ gép van, így nem biztos, hogy mindenkinek lesz szabad gépe. A könyvtáros szeretne a lehető legkevesebb diáknak nemet mondani. Segítsünk neki egy programmal, amely megadja, hogy legkevesebb hány diáknak és kiknek kell nemet mondania.

Bemenet: Az első sor tartalmazza a diákok $\displaystyle N$ számát és a gépek $\displaystyle M$ számát. A diákokat 0-tól $\displaystyle N-1$-ig indexeljük. A következő $\displaystyle N$ sor mindegyike egy $\displaystyle a$ és egy $\displaystyle b$ számot tartalmaz, amely leírja, hogy az adott diák mettől meddig szeretne gépezni.

Kimenet: Az első sor tartalmazza azt a minimum számot, ahány diáknak nemet kell mondani. A következő sor tartalmazza azon diákok indexét növekvő sorrendben, akiknek nemet kell mondani. Több lehetséges megoldás, vagyis azonos számú elutasított diák esetén a legkisebb indexű diákokat fogadja a könyvtáros.

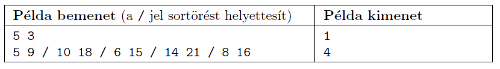
Korlátok: $\displaystyle 1\le N,M\le {10}^{5}$, $\displaystyle 0\le a,b\le {10}^{9}$, egy diákra: $\displaystyle a<b$.

Időkorlát: 0,5 mp.

Értékelés: A pontok 20%-a kapható, ha $\displaystyle N\cdot M\le {10}^{6}$; további 20% kapható, ha $\displaystyle b-a=1$ minden diákra; további 20% kapható, ha $\displaystyle a,b\le {10}^{6}$ minden diákra; további 40% kapható az eredeti korlátokra.

Beküldendő egy is32.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy melyik fejlesztő környezetben futtatható.

(10 pont)

statisztika

S-jelű feladatok A beküldési határidő 2019. február 11-én LEJÁRT.

S. 131. Egy cukrászatban különböző díszítéseket lehet kérni a tortákra. Összesen $\displaystyle N$ különböző dísz van, egy tortára pontosan $\displaystyle M$ darab dísznek kell kerülnie. Hogy ne legyen egyhangú a torta, egyféle díszből legföljebb $\displaystyle K$ darab kerülhet egy tortára. Ezen feltételek mellett a cukrászat elkészítette az összes különböző díszítésű tortát, mindegyikből pontosan egyet. Ezután a tortákat autók szállították el különböző cukrászdákba. Minden autó pontosan $\displaystyle P$ tortát tudott szállítani, se többet, se kevesebbet. A maradék tortákat, amiket nem tudtak elszállítani, a cukrászat dolgozói fogyasztották el. Adjuk meg, hogy hány tortát kaptak a dolgozók, illetve a torták számának $\displaystyle P$-vel való osztási maradékát.

Bemenet: egyetlen sor tartalmazza az $\displaystyle N$, $\displaystyle K$, $\displaystyle M$, $\displaystyle P$ számokat.

Kimenet: egy egész számot tartalmaz, amely megadja a dolgozók által kapott torták $\displaystyle P$ szerinti maradékát.

Példa:

Korlátok: $\displaystyle 1 \le N, K M \le 10^{17}$; $\displaystyle K < M$; $\displaystyle 2 \le P < 10^6$. Időlimit: 0,5 másodperc.

Értékelés: a pontok 20%-a kapható, ha $\displaystyle N,K,M \le 20$; további $\displaystyle 20\%$ kapható, ha $\displaystyle N,K,M \le 10^6$; további 10% kapható, ha $\displaystyle P$ prím; további 10% kapható, ha $\displaystyle M$ osztható $\displaystyle K$-val; további 40% kapható az eredeti korlátokra.

Beküldendő egy s119.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.

(10 pont)

statisztika