A KöMaL 2019. januári matematika feladatai

K-jelű feladatok A beküldési határidő 2019. február 11-én LEJÁRT.

---

K. 609. Hány óra van most, ha 50 perccel ezelőtt négyszer annyi perccel múlt 3 óra, mint amennyi még 6 óráig hátravan? (Ugyanazon a délutánon értve az időpontokat.)

(6 pont)

megoldás, statisztika

---

K. 610. Három méter magasra vezető 1 méter széles tömör beton lépcsőt kell építenünk, egyforma magas lépcsőfokokkal. Minden lépcsőfoknak van egy magassága ($\displaystyle m$), és egy úgynevezett lépésmélysége ($\displaystyle l$), ahogy az ábra mutatja. A lépcsőfokoknál előírás, hogy $\displaystyle 2m+l=64$ cm, valamint hogy a lépcsőfok ne legyen magasabb, mint amekkora a lépésmélysége. Legkevesebb hány lépcsőfokra lesz szükség? Mennyi betonra lesz szükség a minimális darabszámú lépcsőfokból álló lépcsőhöz?

(6 pont)

megoldás, statisztika

---

K. 611. Párokba lehet-e rendezni 1-től 50-ig az egész számokat úgy, hogy minden párban a számok összege más-más prímszám legyen?

(6 pont)

megoldás, statisztika

---

K. 612. Keressük meg az összes olyan pozitív egész $\displaystyle n$ számot, melyre $\displaystyle n + 125$ és $\displaystyle n + 201$ is négyzetszám.

(6 pont)

megoldás, statisztika

---

K. 613. Egy táblára ketten felváltva felírnak egy-egy 10-nél nem nagyobb pozitív egész számot. A szabály szerint olyan számot nem lehet felírni, amely a táblára már felírt számok valamelyikének osztója. Aki nem tud új számot felírni, veszít. Melyik játékosnak van nyerő stratégiája?

Javasolta: Loránt László

(6 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2019. február 11-én LEJÁRT.

---

C. 1518. Hány olyan $\displaystyle 13$-jegyű pozitív egész szám van, ami csak a $\displaystyle 3$, $\displaystyle 6$, $\displaystyle 9$ számjegyeket tartalmazza, és bármely két szomszédos számjegyének különbsége $\displaystyle 3$?

(5 pont)

megoldás, statisztika

---

C. 1519. Egy háromszög két oldalának hossza $\displaystyle 31$ és $\displaystyle 22$, a hozzájuk tartozó súlyvonalak merőlegesek egymásra. Mekkora a harmadik oldal?

(5 pont)

megoldás, statisztika

---

C. 1520. Határozzuk meg a $\displaystyle 2^{2019}+2019^2$ szám utolsó két számjegyét.

(5 pont)

megoldás, statisztika

---

C. 1521. Az $\displaystyle O$ középpontú kört $\displaystyle E$-ben belülről érinti egy feleakkora sugarú kör. Egy $\displaystyle O$-ból induló félegyenes a nagy kört $\displaystyle P$-ben, a kis kört pedig az $\displaystyle O$-tól különböző $\displaystyle R$ pontban metszi. Bizonyítsuk be, hogy az $\displaystyle \widehat{EP}$ és az $\displaystyle \widehat{ER}$ körív hossza megegyezik.

(5 pont)

megoldás, statisztika

---

C. 1522. A pozitív egész számokat három sorba rendezzük a következőképpen:

$$\begin{align*} &1 \ \ 4 \ \ 7 \ \ 10 \ \ 13 \ \ 16\ldots\\ &2 \ \ 5 \ \ 8 \ \ 11 \ \ 14 \ \ 17\ldots\\ &3 \ \ 6 \ \ 9 \ \ 12 \ \ 15 \ \ 18\ldots \end{align*}$$

Igazoljuk, hogy mindhárom sorból kiválasztható egy-egy végtelen mértani sorozat.

(5 pont)

megoldás, statisztika

---

C. 1523. Egy konvex négyszöget az átlóival háromszögekre bontunk. Mutassuk meg, hogy ha a négy háromszög területei között pontosan háromféle érték fordul elő, akkor a négyszög trapéz.

(5 pont)

megoldás, statisztika

---

C. 1524. Legyenek $\displaystyle N$ és $\displaystyle M$ pozitív egész számok, továbbá $\displaystyle p$ és $\displaystyle q$ különböző prímszámok. Tegyük fel, hogy $\displaystyle N+M$ ötjegyű, $\displaystyle N$-nek osztója a $\displaystyle p$, és osztóinak száma $\displaystyle q$, ugyanakkor $\displaystyle M$ osztható $\displaystyle q$-val, és osztóinak száma $\displaystyle p$. Határozzuk meg $\displaystyle N$ és $\displaystyle M$ lehetséges értékeit.

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2019. február 11-én LEJÁRT.

---

B. 4998. Az általános iskolai Logikai Készlet $\displaystyle 48$ műanyag lapocskából áll. A lapokat négy jellemző tulajdonság írja le: egy-egy elem mérete lehet kicsi vagy nagy; lehet sima vagy lyukas; a színe piros, sárga, kék vagy zöld; alakja kör, négyzet vagy háromszög. A tulajdonságok minden lehetséges kombinációja (pl. kicsi kék lyukas kör) pontosan egy lapocskára igaz. Hány olyan $\displaystyle x$ eleme van a készletnek, amelyhez található a készletnek olyan $\displaystyle y$ eleme, amelyre az alábbi két feltétel mindegyike teljesül?

1. Ha $\displaystyle x$ sima vagy piros, akkor $\displaystyle y$ kicsi sárga négyzet.

2. Ha $\displaystyle y$ kicsi vagy kék, akkor $\displaystyle x$ zöld háromszög, vagy pedig valamilyen sima alakzat.

ELTE TTK elsőéves analízis zárthelyi dolgozat alapján

(4 pont)

megoldás, statisztika

---

B. 4999. Az $\displaystyle ABC$ háromszög beírt körének középpontja $\displaystyle O$, érintési pontjai $\displaystyle A_1$, $\displaystyle B_1$, $\displaystyle C_1$, hozzáírt köreinek érintési pontjai $\displaystyle A_2$, $\displaystyle B_2$, $\displaystyle C_2$ az ábra szerint. Mutassuk meg, hogy az $\displaystyle OA_1 A_2$, $\displaystyle OB_1 B_2$ és $\displaystyle OC_1 C_2$ háromszögek közül valamelyiknek a területe egyenlő a másik két háromszög területének összegével.

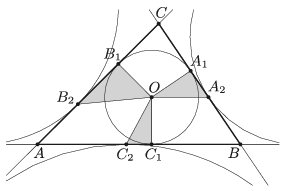
Javasolta: Kocsis Szilveszter (Budapest)

(3 pont)

megoldás, statisztika

---

B. 5000. Adott $\displaystyle 4999$ különböző egész szám, az egyik a $\displaystyle 42$. Igazoljuk, hogy kiválasztható közülük néhány, amelyek összege osztható $\displaystyle 5000$-rel.

(4 pont)

megoldás, statisztika

---

B. 5001. Egy egyenlő szárú háromszög alapja $\displaystyle a$, szárszöge $\displaystyle 120^{\circ}$-nál kisebb, az alaphoz tartozó magassága $\displaystyle m$. A háromszög mindegyik csúcsát tükrözzük a szemközti oldalegyenesre. A három kapott pont egy másik egyenlő szárú háromszöget alkot, amelynek alapja $\displaystyle a'$, alaphoz tartozó magassága pedig $\displaystyle m'$. Mutassuk meg, hogy

$\displaystyle \frac{a'}{a}+\frac{m'}{m}=4.$

Javasolta: Bártfai Pál (Budapest)

(3 pont)

megoldás, statisztika

---

B. 5002. Az $\displaystyle x^3 +a x^2 + bx + c$ harmadfokú polinom grafikonja a különböző $\displaystyle P_1$, $\displaystyle P_2$, $\displaystyle P_3$, $\displaystyle P_4$, $\displaystyle P_5$, $\displaystyle P_6$ pontokban metszi az origó középpontú, $\displaystyle 10$ egység sugarú kört. Fejezzük ki a $\displaystyle P_1$, $\displaystyle P_2$, $\displaystyle P_3$, $\displaystyle P_4$, $\displaystyle P_5$, $\displaystyle P_6$ pontrendszer súlypontjának koordinátáit az $\displaystyle a$, $\displaystyle b$, $\displaystyle c$ együtthatókkal.

(5 pont)

megoldás, statisztika

---

B. 5003. Igaz-e, hogy ha egy tetraéder hat élfelezőpontja közül öt illeszkedik egy gömbre, akkor a hatodik élfelezőpont is illeszkedik ugyanerre a gömbre?

(5 pont)

megoldás, statisztika

---

B. 5004. $\displaystyle 2n$ egymást követő egész szám között legfeljebb hány olyan lehet, amely osztható az $\displaystyle n+1$, $\displaystyle n+2$, $\displaystyle \ldots$, $\displaystyle 2n$ számok közül legalább az egyikkel?

Javasolta: Róka Sándor (Nyíregyháza)

(6 pont)

megoldás, statisztika

---

B. 5005. Az $\displaystyle ABC$ hegyesszögű háromszög magasságvonalainak talppontja a $\displaystyle BC$, $\displaystyle CA$, $\displaystyle AB$ oldalakon rendre $\displaystyle D$, $\displaystyle E$, $\displaystyle F$, az $\displaystyle ABC$ háromszög magasságpontja $\displaystyle M$. Jelölje az $\displaystyle AB$, mint átmérő fölé rajzolt kört $\displaystyle k_1$, a $\displaystyle DEM$ háromszög körülírt körét $\displaystyle k_2$. Vegyük föl a $\displaystyle k_2$ körnek a $\displaystyle D$ pontot nem tartalmazó $\displaystyle EM$ ívén az $\displaystyle E$, $\displaystyle M$ pontoktól különböző $\displaystyle P$ pontot. Messe a $\displaystyle DP$ egyenes a $\displaystyle k_1$ kört másodszor a $\displaystyle Q$ pontban, és legyen a $\displaystyle PQ$ szakasz felezőpontja $\displaystyle R$. Mutassuk meg, hogy az $\displaystyle AQ$, $\displaystyle MP$, $\displaystyle FR$ egyenesek egy pontban metszik egymást.

Javasolta: Bíró Bálint (Eger)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2019. február 11-én LEJÁRT.

---

A. 740. Egy $\displaystyle k\times k$-as számtáblázatban az $\displaystyle 1,2,\ldots,m$ számok pontosan egyszer szerepelnek, míg a maradék helyen $\displaystyle 0$ áll. Tegyük fel, hogy az összes sorösszeg és oszlopösszeg azonos. Legalább mekkora $\displaystyle m$ értéke, ha $\displaystyle k=3^n$ ($\displaystyle n\in\mathbb{N^+}$)?

Javasolta: Sztranyák Attila és Erben Péter,
a 2017. évi Kalmár-verseny feladata alapján

(7 pont)

statisztika

---

A. 741. Legyen $\displaystyle f$ olyan pozitív egészeken értelmezett függvény, melyre $\displaystyle f(n)\ge 0$ és $\displaystyle f(n)\le f(n+1)$ minden $\displaystyle n$-re. Igazoljuk, hogy ha

$\displaystyle \sum_{n=1}^\infty \frac{f(n)}{n^2}$

divergens, akkor létezik olyan $\displaystyle a_1,a_2,\dots$ sorozat, amelyre $\displaystyle \frac{a_n}{n}$ felvesz minden racionális számot értékként, míg

$\displaystyle a_{n+m}\le a_n+a_m+f(n+m)$

teljesül minden $\displaystyle n$, $\displaystyle m$ párra.

Schweitzer-feladat nyomán

(7 pont)

megoldás, statisztika

---

A. 742. Az $\displaystyle \Omega$ körbe írt $\displaystyle ABCD$ konvex húrnégyszög $\displaystyle AD$ és $\displaystyle BC$ oldalegyenesei az $\displaystyle E$ pontban metszik egymást. Legyen $\displaystyle M$ és $\displaystyle N$ a többi csúcsot nem tartalmazó $\displaystyle AB$, illetve $\displaystyle CD$ körívek felezőpontja, továbbá legyen $\displaystyle I$, $\displaystyle J$, $\displaystyle K$, és $\displaystyle L$ rendre az $\displaystyle ABD$, a $\displaystyle ABC$, a $\displaystyle BCD$, illetve a $\displaystyle CDA$ háromszögbe írt kör középpontja. Messe $\displaystyle \Omega$ az $\displaystyle IJM$ és $\displaystyle KLN$ köröket másodszor az $\displaystyle U\ne M$, illetve a $\displaystyle V\ne N$ pontban. Mutassuk meg, hogy az $\displaystyle E$, $\displaystyle U$ és $\displaystyle V$ pontok egy egyenesre illeszkednek.

(7 pont)

megoldás, statisztika