A KöMaL 2019. decemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2020. január 10-én LEJÁRT. |
I. 496. A processzorok bitműveletek segítségével sokszor gazdaságosabban és gyorsabban végzik el két egész szám szorzását, mint más módon. Tízes számrendszerben egy szám végére 0-t írva annak 10-szeresét kapjuk, míg kettes számrendszerben az eredeti szám 2-szeresét. Ha tehát egy bináris számot eltolunk 3-mal a nagyobb helyiértékek felé, miközben a szám végére három 0-át írunk, akkor egy 8-cal történő szorzást végzünk. Ha a kapott értékhez még hozzáadjuk az eredeti számot, akkor valójában 9-cel szorzunk.
Ezek alapján minden egész számmal történő szorzás megvalósítható bizonyos számú eltolás, a közben kapott értékek tárolása, és valahány összeadás segítségével. Például az \displaystyle x\cdot 29 fölírható
\begin{align*} x\cdot (28+1)& =x\cdot (2\cdot 14+1)=x\cdot (2\cdot 2\cdot 7+1)=x\cdot \big(2\cdot 2\cdot (6+1)+1\big)=\\ &= x\cdot \big(2\cdot 2\cdot (2\cdot 3+1)+1\big)= x\cdot \big(2\cdot 2\cdot \big(2\cdot (2+1)+1\big)+1\big) \end{align*}alakban. Ha ezt fölbontjuk, akkor az \displaystyle x\cdot 2\cdot 2\cdot 2\cdot 2 + x\cdot 2\cdot 2\cdot 2 + x\cdot 2\cdot 2 + x kifejezést kapjuk, ahol csak 2-vel való szorzás (tehát eltolás), illetve összeadás szerepel.
Tegyük föl, hogy a részeredmények tárolásához elegendő hely áll rendelkezésre. Adjuk meg, hogy ezzel a módszerrel végezve hány eltolás és hány összeadás szükséges egy adott számmal történő szorzás elvégzéséhez. A 29-cel való szorzáshoz például ki kell számítanunk az \displaystyle x\cdot 2, \displaystyle x\cdot 2\cdot 2, \displaystyle x\cdot 2\cdot 2\cdot 2, \displaystyle x\cdot 2\cdot 2\cdot 2\cdot 2 értékét, amelyekhez összesen 4 eltolás szükséges, és ezután kell még három összeadás.
A program a standard bemenet első sorából olvassa be a szorzót (pozitív egész), majd írja ki a standard kimenet egyetlen sorába elsőként az eltolások számát, majd szóközzel elválasztva az összeadások számát.
Beküldendő egy i496.zip tömörített állományban a program forráskódja és egy rövid leírás, ami megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 497. (É). Ebben a feladatban azt vizsgáljuk, hogy egy adott gimnáziumba jelentkező tanulók milyen eredményt értek el a felvételi vizsgán az adott városban felvételiző összes tanuló eredményéhez viszonyítva.
A felvételi vizsga írásban, két tantárgyból történik: magyarból és matematikából. Mindkét tantárgyból legfeljebb 50 pont szerezhető.
Rendelkezésünkre áll egy táblázat, amelynek első oszlopa a lehetséges pontszámokat tartalmazza 0-tól 50-ig. A mellette lévő négy oszlop pedig rendre megmutatja, hogy hány tanuló ért el ennyi pontot magyarból a városban, illetve az adott iskolában; valamint matematikából a városban, illetve az adott iskolában.
1. Töltsük be a táblázatkezelő program egyik munkalapjára az A1 cellától kezdve a felv.txt adatfájlt, majd mentsük a munkafüzetet elemzes néven a program alapértelmezett formátumában.
2. Határozzuk meg a K5:L5 tartományban, hogy hány tanuló írt felvételi dolgozatot magyarból és matematikából az adott városban, illetve az K8:L8 tartományban azt, hogy közülük hány tanuló jelentkezett az adott iskolába.
3. Határozzuk meg a K6:L6, illetve a K9:L9 tartományban a tanulók átlagos pontszámát az egyes tantárgyakból a város összes tanulója, illetve az adott iskolába jelentkező tanulók esetén. Az eredményeket két tizedesjegyre formázva jelenítsük meg.
4. Mennyivel nagyobb az adott iskolába jelentkező tanulók átlagos pontszáma, mint a város összes tanulójáé? Az eredményt képlettel írassuk tantárgyanként a K11:L11 tartományba.
5. Határozzuk meg tantárgyanként a város valamennyi felvételizője, illetve az adott iskolába jelentkező tanulók esetén is tantárgyanként, hogy melyik pontszám volt a leggyakoribb. Az eredményt képlettel adjuk meg a K7:L7, illetve a K10:L10 tartomány celláiban.
6. Szeretnénk megvizsgálni, hogy mely pontszámok fordulnak elő nagyobb gyakorisággal az adott iskolába jelentkező tanulók esetén, mint a város összes felvételizője esetén. Feltételes formázás alkalmazásával emeljük ki
\displaystyle a) a C4:D54 tartományban halványpiros háttérrel az azokhoz a pontszámokhoz tartozó sorokat, amelyekben a pontszámok relatív gyakorisága magyarból nagyobb volt az adott iskolába jelentkező tanulók esetén, mint a város összes tanulója esetén;
\displaystyle b) a G4:H54 tartományban halványzöld háttérrel az azokhoz a pontszámokhoz tartozó sorokat, amelyekben a pontszámok relatív gyakorisága matematikából nagyobb volt az adott iskolába jelentkező tanulók esetén, mint a város összes tanulója esetén.
7. Az iskola igazgatója 5 pontos sávonként is szeretné összehasonlítani az eredményeket, de csak azok az adatok érdeklik, amelyek 20 pontnál nagyobbak. Az egyes sávok alsó és felső határát az I18:J23 tartomány tartalmazza. Másolható képlet segítségével határozzuk meg a K18:K23 tartomány celláiban, hogy a tanulók hány százaléka esik az adott sávba a városban magyar felvételi vizsgát írt tanulók esetén. Hasonló módon végezzük el a számítást az adott iskolába jelentkező tanulók esetén is az L18:L23 tartományban, valamint a matematika tantárgyra vonatkozóan is az M17:N23 tartományban. Ügyeljünk arra, hogy csak a 20 pontot meghaladó tanulók képezik a mintát!
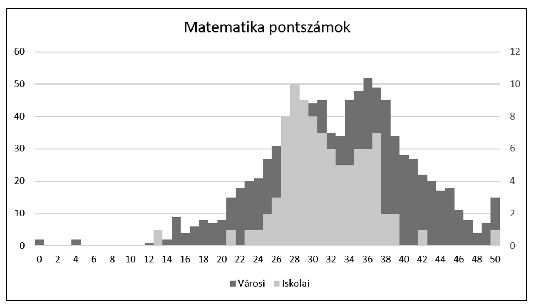
8. Ábrázoljuk csoportosított oszlopdiagramon a tanulók iskolai és városi matematika pontszámának megoszlását úgy, hogy az oszlopok érjenek össze. Az iskolai adatok áttekinthetőbb elrendezéséhez alkalmazzunk második értéktengelyt. A diagram címe ,,Matematika pontszámok'' legyen.

9. Formázzuk meg az I4:L11 tartományt a mintának megfelelően!
Beküldendő egy tömörített i497.zip állományban a megoldást adó táblázatkezelő munkafüzet és egy rövid dokumentáció, amely megadja a felhasznált táblázatkelő nevét és verzióját.
Letölthető állomány: felv.txt
(10 pont)
I. 498. (É). Egy szabadstrand vízibicikli-kölcsönzőjében kölcsönzéskor rögzítik a kölcsönző nevét (lehet becenév is), az elvitt jármű azonosítóját (\displaystyle A, \displaystyle B, \displaystyle C, \displaystyle D, \displaystyle E, \displaystyle F, \displaystyle G), az elvitel óráját és percét, valamint a visszahozatal óráját és percét. Például:
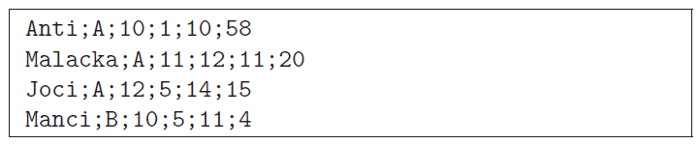
Egy időpontban csak egy jármű indulhat vagy érkezhet. A járművekért minden megkezdett fél óra után 1500 Ft-ot kell fizetni. A kölcsönzés idejébe az első és az utolsó perc is beleszámít.
Az adatokat a – weblapunkról letölthető – vizdat.csv nevű, pontosvesszővel tagolt szöveges állomány tartalmazza. Feltételezhetjük, hogy a napi kölcsönzések száma nem haladja meg a 100-at.
Készítsünk programot i498 néven a következő feladatok megoldására. A program futása során a képernyőre való kiíráskor utaljunk a feladat sorszámára.
1. Olvassuk be a vizdat.csv fájlból és tároljuk el a napi kölcsönzések adatait.
2. Kérjünk be egy nevet és írassuk ki, hogy az illető aznap mettől meddig vette igénybe a kölcsönző szolgáltatásait. Elképzelhető, hogy az illető többször is kölcsönzött aznap, ebben az esetben minden kölcsönzés adatát írassuk ki. Ha aznap egyszer sem kölcsönzött, akkor a Nem volt ilyen nevű kölcsönző! szöveg jelenjen meg.
3. Kérjünk be egy időpontot az óra és a perc megadásával, majd írassuk ki a képernyőre, hogy ekkor mely járművek voltak vízen, és azokat kik kölcsönözték ki.
4. Határozzuk meg a napi bevétel összegét, és írassuk ki a képernyőre.
5. Melyik járművet hányszor kölcsönözték ki aznap? A választ a minta szerinti elrendezésben írassuk ki a képernyőre:

6. Melyik jármű után fizették a legnagyobb kölcsönzési díjat? Írassuk ki a képernyőre órában megadva a fizetett időt és a jármű azonosítóját. (Vegyük figyelembe, hogy minden megkezdett fél óra után a teljes fél órát ki kell fizetni.) Ha több ilyen jármű volt, mindegyik azonosítója jelenjen meg.
7. Néhány strandoló nem tudott járművet kölcsönözni, mert éppen az összeset elvitték. Mikor volt ilyen időszak? Jelenítsük meg valamennyi időtartamot a képernyőn kezdés óra, kezdés perc, vége óra, vége perc formátumban.
8. Sajnos az \displaystyle F jelű járművet napközben valaki használat közben megrongálta. Készítsünk egy szöveges állományt, amely tartalmazza a lehetséges elkövetőket és azt, hogy mettől meddig volt náluk a jármű. Az adatokat a következő formában írassuk a fjarmu.txt fájlba:

Beküldendő egy i498.zip tömörített állományban a program forráskódja és egy rövid leírás, ami megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
Letölthető állomány: Vizdat.csv.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2020. január 10-én LEJÁRT. |
I/S. 40. Egy nap \displaystyle N matematikus moziba megy. A moziban \displaystyle M darab szék van egy sorban (1-től \displaystyle M-ig megszámozva). Mindannyian egy sorban ülnek le. Mindenki megmondja, hogy minimum melyik sorszámú székre és maximum melyik sorszámú székre hajlandó leülni. Nincs olyan szék, ahova ketten is leülhetnének. Azért, hogy kényelmesen elférjenek, megpróbálnak a lehető legtávolabb leülni egymástól. Még pontosabban: arra törekednek, hogy a két egymáshoz legközelebb ülő matematikus távolsága (a székek számának különbsége) a lehető legnagyobb legyen. Adjuk meg, hogy mekkora ez a legnagyobb távolság.
Bemenet: az első sor tartalmazza \displaystyle N és \displaystyle M értékét. A következő \displaystyle N sor mindegyike egy \displaystyle a_{i}, b_{i} számpárt tartalmaz, ami azt jelenti, hogy az \displaystyle i-edik matematikus olyan székre szeretne leülni, amelynek száma legalább \displaystyle a_{i} és legfeljebb \displaystyle b_{i}. Kimenet: a program adjon meg egyetlen számot, két legközelebbi matematikus maximális távolságát.
Példa:

Korlátok: \displaystyle 3\le N\le {10}^{5}, \displaystyle 0\le M\le {10}^{9}. Időkorlát: 0,3 mp.
Értékelés: a pontok 50%-a kapható, ha \displaystyle 2\le N\le {10}^{2}.
Beküldendő egy is40.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2020. január 10-én LEJÁRT. |
S. 139. Adott \displaystyle N darab pozitív egész szám. Adjuk meg, hogy hány olyan számpár van közöttük, amelyek tagjai relatív prímek.
Bemenet: az első sor tartalmazza az \displaystyle N értékét. A második sor tartalmazza szóközökkel elválasztva az \displaystyle N darab pozitív egészet.
Kimenet: egyetlen sor, mely a relatív prím számpárok számát tartalmazza.
Példa:

Korlátok: \displaystyle 3\le N\le 50\, 000, \displaystyle 1\le \text{számok}\le 500\, 000. Időkorlát: 0,3 mp.
Értékelés: a pontok 30%-a kapható, ha \displaystyle N\le 1000.
Beküldendő egy s139.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.
|
|

