A KöMaL 2020. májusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2020. június 10-én LEJÁRT. |
M. 396. Mérjük meg a celluxszalag vastagságát!
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2020. június 10-én LEJÁRT. |
G. 709. Tarzan az íjával célba veszi Maki majmot a fán. Az ellövés pillanatában a nyílvessző éppen a Maki kezében lévő banánra mutat. Ugyanebben a pillanatban a majom ijedtében elejti a banánt. Mit talál el a nyílvessző, ha a légellenállástól eltekinthetünk?
(3 pont)
G. 710. Anna és Zalán osztálytársak, egy egyenes utcában két különböző házban laknak. Minden reggel ugyanakkor lépnek ki a kapun, és egyenletesen haladva mennek az iskolába. Zalán távolabb lakik az iskolától, de ő a gyorsabb, bizonyos idő alatt utoléri Annát. Egyik alkalommal Anna hamarabb szeretne találkozni Zalánnal, és emiatt egymás felé indulnak el. Ekkor a szokásosnál ötször hamarabb találkoznak. Hányszor gyorsabb Zalán Annánál?
(3 pont)
G. 711. Egy zárt, föld alatti üreg egy kürtővel csatlakozik a külvilághoz. Az üreg bizonyos részeiben víz van. Határozzuk meg a nyomást az ábrán feltüntetett A, B, C és D pontokban!
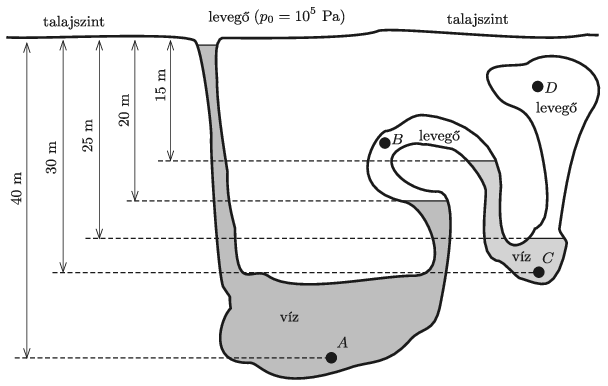
(4 pont)
G. 712. Állítás: Nem túlságosan alacsony hőmérsékleten a fémek moláris hőkapacitása közelítőleg azonos értékű, mégpedig 3R=24,9 J/(molK), ahol R a Regnault-konstans, ismertebb nevén a gázállandó. Vizsgáljuk meg, hány százalékos pontossággal teljesül ez az állítás alumínium, arany, ezüst, réz és vas esetében!
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2020. június 10-én LEJÁRT. |
P. 5230. A rétegelt acél (hibásan damaszkuszi acél) két eltérő széntartalmú réteg összekovácsolásával készül, amit – a leveles tésztához hasonlóan – duplájára nyújtanak, majd félbe hajtanak. Hányszor kellene megismételni ezt a műveletet, hogy egyetlen réteg vastagsága atomi méretű legyen, ha kezdetben az acél vastagsága 3 mm volt?
Közli: Vass Miklós, Budapest
(3 pont)
P. 5231. Egy almát a szára tövénél három egyforma hosszú, egyforma teherbírású fonálon tartunk. A fonalak felső végeit vízszintes síkban lassan távolítjuk egymástól úgy, hogy a fonalak páronként mindig ugyanakkora szöget zárnak be egymással. A fonalak akkor szakadnak el, amikor páronként éppen merőlegesek egymásra. Ha két ugyanilyen fonálhoz erősítenénk ugyanezt az almát, majd a fonalak felső végeit ugyanúgy vízszintes síkban távolítanánk egymástól, milyen szöget zárnának be egymással a fonalak, amikor elszakadnának?
Közli: Nagy Piroska Mária, Budapest
(4 pont)
P. 5232. Vékony falú, celloidból készült keljfeljancsi alsó gömbjének sugara 3 cm. A játék belsejébe, alul egy 2 cm átmérőjű acélgolyót rögzítettek. A keljfeljancsit lassan kitérítjük úgy, hogy szimmetriatengelye a függőlegessel 30∘-os szöget zárjon be. Mekkora lesz a játék szögsebessége abban a pillanatban, amikor a tengelye átlendül a függőleges helyzeten? (A tapadó súrlódás elég nagy, a játék nem csúszik meg a talajon. A gördülő súrlódástól és a közegellenállástól eltekinthetünk.)
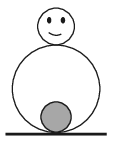
Közli: Kis Tamás, Heves
(4 pont)
P. 5233. Egy levelibéka egy tőle vízszintesen s távolságra, de h magasságban lévő levélre akar a talajról felugrani. Milyen irányba és mekkora sebességgel kell elrugaszkodnia, hogy a legkevesebb energiára legyen ehhez szüksége?
Közli: Woynarovich Ferenc, Budapest
(5 pont)
P. 5234. Az ábra szerinti, függőleges szimmetriatengelyű, hengeres tartályt felül egy súlytalannak tekinthető dugattyú zár el. A 7 dm3 térfogatú edényben nincs levegő, csak T hőmérsékletű, telített vízgőzt tartalmaz. Mekkora munkát végzünk, ha a dugattyút lassan addig nyomjuk le, míg az folyadékba nem ütközik? A folyamat során az egész rendszer hőmérséklete állandó. Számítsuk ki és ábrázoljuk a végzett munkát a T hőmérséklet függvényében, ahol 100∘C≤T≤370∘C. (A telített vízgőz nyomására, sűrűségére és a víz sűrűségére vonatkozó adatokat vegyük a Négyjegyű függvénytáblázatokból!)
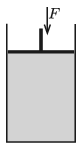
Közli: Légrádi Imre, Sopron
(4 pont)
P. 5235. n=2 mol anyagmennyiségű, egyatomos ideális gáz az ábrán látható A→P→B folyamatot végzi. A gáz hőmérséklete a kiinduló állapotban T1=280 K, a végállapotban T2=4T1. Az AP szakasz párhuzamos a V tengellyel, a BC szakasz meghosszabbítása átmegy az origón, a P pont pedig a BC szakasz felezőpontja.
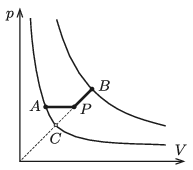
a) Határozzuk meg a gáz hőmérsékletét a P állapotban!
b) Mennyi hőt vesz fel a gáz az A→P→B folyamatban?
Közli: Kotek László, Pécs
(5 pont)
P. 5236. Egy üvegprizma egyik lapjára merőlegesen esik egy fénysugár, amely a prizma másik oldalán, felül még nem tud kilépni, mert az a rész tükröző anyaggal van bevonva. A prizma első oldalát a belépési pont alatt ugyancsak tükröző anyaggal vonták be, ezért a fény ezen a részen sem tud kilépni az üvegből, hanem visszaverődik. Végül a túlsó oldalon kilépő fénysugár a prizmához érkező fénysugár irányához képest 40∘-kal térül el. Mekkora a prizma törőszöge, ha az anyagának törésmutatója 1,5?
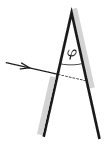
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 5237. Az ábrán látható ellenállásrendszer A pontjában 40 mA erősségű áram folyik be, és a B pontnál folyik ki.

a) Mekkora áram folyik át az egyes ellenállásokon?
b) Mekkora az egyes ellenállásokra eső elektromos teljesítmény?
c) Mekkora egyetlen ellenállással lehetne helyettesíteni az ellenállásrendszert?
Közli: Simon Péter, Pécs
(4 pont)
P. 5238. Egy m0 tömegű elektromos játékautó m tömegű teherrel a platóján állandó sebességgel halad felfelé egy α hajlásszögű lejtőn. Az r sugarú kerekeket meghajtó villanymotort állandósult állapotban modellezhetjük egy R ellenállással sorosan kapcsolt olyan áramköri elemmel, amelynek U feszültsége a tengely ω szögsebességével arányos (U=γω), az I árama pedig a tengelyek által kifejtett M forgatónyomatékkal arányos (I=M/γ). A kisautó egy olyan teleppel működik, amelynek üresjárati feszültsége U0, belső ellenállása pedig Rb.
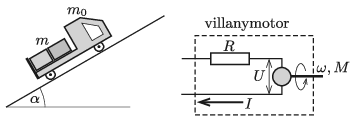
Adatok: m0=300 g, α=30∘, r=2 cm, γ=1,2 Vs, U0=4,5 V, R=0,8 Ω , Rb=1,2 Ω. (A kerekek és a lejtő közötti tapadási súrlódás elég nagy, így az autó nem csúszik meg.)
a) Mekkora állandósult sebességgel halad a kisautó, ha m=600 g teher van a platóján?
b) Mekkora m teher esetén lesz a legjobb a szállítás hatásfoka? (A hatásfokon a teher emelésére fordított energia és a telep által leadott energia hányadosát értjük.)
Közli: Olosz Balázs, Pécs
(5 pont)
P. 5239. Egy vékony, elhanyagolható tömegű, 21 cm hosszú, merev rúd végein egy-egy azonos tömegű, pontszerűnek tekinthető, kicsiny test van. Ezt a rudat a közepénél fogva felfüggesztjük egy olyan vékony, rugalmas szálra, hogy az így kapott torziós inga kis kitérések esetén mérhető lengésideje viszonylag nagy, 600 másodperc legyen. Ezután az ingát belógatjuk két, egyenként 600 kg tömegű, nagy ólomgolyó közé, középre. Az ólomgolyók középpontjai egymástól 70 cm-re vannak. Mennyi lesz az inga lengésideje kis kitérések esetén, ha az ingarúd kezdetben
a) a két golyó középpontját összekötő vízszintes szakaszon van;
b) az előbbi esetre merőleges helyzetű?
Megjegyzés. Hasonló módon határozta meg Eötvös Loránd a gravitációs állandót, két, mintegy 600 kg tömegű ólomhasáb és egy hasonlóan nagy lengésidejű torziós inga segítségével. A feladatban a gravitációs állandó ismert értékének felhasználásával kell a kétféle lengésidőt kiszámítani. (Lásd még a P. 5166. feladat megoldását a KöMaL 2020. évi márciusi számában.)
Közli: Radnai Gyula, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

