A KöMaL 2020. májusi matematika feladatai

C-jelű feladatok A beküldési határidő 2020. június 10-én LEJÁRT.

---

C. 1609. Oldjuk meg az alábbi egyenletrendszert a valós számpárok halmazán:

$$\begin{align*} x+y+\frac xy & =19,\\ \frac{x(x+y)}{y} & =60. \end{align*}$$

(5 pont)

megoldás, statisztika

---

C. 1610. Egy egységsugarú kör $\displaystyle AB$ átmérője és $\displaystyle AC$ húrja $\displaystyle 30^\circ$-os szöget zárnak be egymással. Jelölje $\displaystyle B$ tükörképét a $\displaystyle C$ pontra $\displaystyle B'$. Határozzuk meg a $\displaystyle B'$ pontból a körhöz húzott érintők $\displaystyle AB$ egyenessel való metszéspontjának $\displaystyle B$-től való távolságát.

(5 pont)

megoldás, statisztika

---

C. 1611. Az első 21 pozitív egész szám közül néhányat kiválasztunk úgy, hogy bármely kettő különbségének az abszolút értékét véve ezen értékek között ne legyen két egyforma. Legfeljebb hány különböző érték jöhet létre? Adjunk konkrét példát is erre az esetre.

(5 pont)

megoldás, statisztika

---

C. 1612. Az $\displaystyle A_1A_2A_3A_4A_5A_6A_7$ konvex hétszög egy olyan körbe írható bele, amelynek középpontja a hétszög belsejében van. Bizonyítsuk be, hogy az $\displaystyle A_1$, $\displaystyle A_3$ és $\displaystyle A_5$ csúcsoknál lévő belső szögek összege kisebb $\displaystyle 450^{\circ}$-nál.

(5 pont)

megoldás, statisztika

---

C. 1613. Egy kosárlabda-bajnokságon $\displaystyle n$ csapat vett részt. Bármelyik két csapat pontosan egyszer játszott egymással, döntetlen nem volt. A bajnokság végén az $\displaystyle i$-edik csapatnak $\displaystyle x_i$ győzelme és $\displaystyle y_i$ veresége volt ($\displaystyle i=1,2,\ldots,n$). Bizonyítsuk be, hogy

$\displaystyle x_1^2+x_2^2+\ldots+x_n^2=y_1^2+y_2^2+\ldots+y_n^2.$

(Horvát feladat)

(5 pont)

megoldás, statisztika

---

C. 1614. Egy 30 cm sugarú kör alakú tálca szélén elhelyezünk 12 darab 9 cm átmérőjű, felülről kör alakú muffint úgy, hogy a tálca szélét érintik, és a szomszédosak egyenlő távolságra helyezkednek el egymástól. Mekkora ez a távolság?

(5 pont)

megoldás, statisztika

---

C. 1615. A feladat szövegében változtatás történt a pirossal jelzett helyen. A helyes szöveg:

Juliska nagymamája minden hétfőn sütit süt. Mindig véletlenszerűen választ az általa ismert végtelen sok recept közül, amiknek a $\displaystyle 60\%$-a csokis. Juliska elég válogatós: nagymama csokis sütijeinek csak a $\displaystyle 90\%$-át szereti, a többi sütijének viszont csak $\displaystyle 30\%$-át. Egy különleges hétfőn kétféle sütit is süt a nagymama. Határozzuk meg annak a valószínűségét, hogy Juliska a két süti közül pontosan egyet szeret.

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2020. június 10-én LEJÁRT.

---

B. 5102. Adott a síkban $\displaystyle n$ különböző pont, nem esik mind egy egyenesre. Mutassuk meg, hogy van olyan önmagát nem metsző, zárt töröttvonal, amelynek az adott pontok a csúcsai. (Egy töröttvonal csúcsánál lehet $\displaystyle 180^{\circ}$-os szög is.)

(3 pont)

megoldás, statisztika

---

B. 5103. Tegyük fel, hogy $\displaystyle a$, $\displaystyle b$, $\displaystyle c$, $\displaystyle x$, $\displaystyle y$ és $\displaystyle z$ olyan pozitív számok, amelyekre az $\displaystyle a^2+b^2=c^2$ és az $\displaystyle x^2+y^2=z^2$ egyenlőségek teljesülnek. Igazoljuk, hogy $\displaystyle {(a+x)}^2+{(b+y)}^2\le {(c+z)}^2$, és határozzuk meg, hogy mikor áll fenn az egyenlőség.

Javasolta: Kiss Sándor (Nyíregyháza)

(3 pont)

megoldás, statisztika

---

B. 5104. Legyenek az $\displaystyle ABC$ háromszög beírt körének érintési pontjai az oldalakon $\displaystyle A_1$, $\displaystyle B_1$ és $\displaystyle C_1$, a háromszög köréírt, illetve beírt körének sugara $\displaystyle R$ és $\displaystyle r$. Mutassuk meg, hogy az $\displaystyle A_1B_1C_1$ és $\displaystyle ABC$ háromszögek területének aránya $\displaystyle r:2R$.

(4 pont)

megoldás, statisztika

---

B. 5105. Legyen $\displaystyle n$ pozitív egész. Határozzuk meg azt a legkisebb $\displaystyle k$ számot, ahány színnel bármilyen $\displaystyle n$ csúcsú irányított egyszerű gráf élei színezhetők úgy, hogy ne legyen benne egyszínű kör.

Javasolta: Szabó Kornél (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 11. évf.)

(4 pont)

megoldás, statisztika

---

B. 5106. Felírjuk a táblára az $\displaystyle n+1, n+2, \ldots, 2n$ számokat ($\displaystyle n\ge2$), majd a következő lépést ismételgetjük: kiválasztunk két számot ($\displaystyle x$ és $\displaystyle y$) a táblán, letöröljük őket, és helyettük felírjuk az $\displaystyle x+y+\sqrt{x^2+y^2}$ és $\displaystyle x+y-\sqrt{x^2+y^2}$ számokat. Igazoljuk, hogy soha nem írhatunk a táblára $\displaystyle 1{,}442$-nél kisebb számot.

(5 pont)

megoldás, statisztika

---

B. 5107. Az $\displaystyle ABCD$ húrnégyszögben az átlók metszéspontja $\displaystyle F$, az $\displaystyle AB$ és $\displaystyle CD$ oldalegyenesek metszéspontja $\displaystyle E$, az $\displaystyle EF$ szakasz felezőpontja $\displaystyle G$, a $\displaystyle BF$ szakasz felezőpontja $\displaystyle H$, a $\displaystyle BC$ oldal felezőpontja pedig $\displaystyle I$. Mutassuk meg, hogy $\displaystyle {GFD\sphericalangle=GIH\sphericalangle}$.

(6 pont)

megoldás, statisztika

---

B. 5108. Az $\displaystyle A$, $\displaystyle B_1$, $\displaystyle B_2$, $\displaystyle B_3$, $\displaystyle C_1$, $\displaystyle C_2$, $\displaystyle C_3$ pontok ebben a sorrendben egy egyenesen vannak. Az egyenes egyik oldalán, az egyenesre merőlegesen rajzoljuk meg a $\displaystyle B_i$ pontból induló $\displaystyle b_i$ félegyeneseket és az $\displaystyle AC_i$ átmérőjű $\displaystyle c_i$ félköröket ($\displaystyle i=1,2,3$). Igazoljuk, hogy ha a $\displaystyle b_1$, $\displaystyle c_1$, $\displaystyle b_2$, $\displaystyle c_2$ görbék által határolt tartományba és a $\displaystyle b_2$, $\displaystyle c_2$, $\displaystyle b_3$, $\displaystyle c_3$ által határolt tartományba egy-egy kört lehet írni, akkor a $\displaystyle b_1$, $\displaystyle c_1$, $\displaystyle b_3$, $\displaystyle c_3$ által határolt tartományba is kört lehet írni.

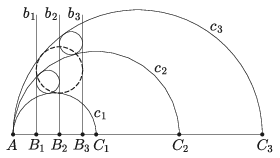
(5 pont)

megoldás, statisztika

---

B. 5109. Legyen

$\displaystyle x_1 = 2, \quad x_2 = 7, \quad x_{n+1} = 4 x_n - x_{n-1} \quad (n=2,3,\ldots).$

Van-e négyzetszám ebben a sorozatban?

Javasolta: George Stoica (Saint John, Canada)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2020. június 10-én LEJÁRT.

---

A. 777. Egy $\displaystyle n$ pontú, síkbarajzolt véges $\displaystyle G(V,E)$ gráfra jelölje $\displaystyle x(e)$ azon élek számát, melyek keresztezik az $\displaystyle e$ élt. Bizonyítandó, hogy

$\displaystyle \sum_{e\in E} \frac{1}{x(e)+1}\le 3n-6.$

Javasolta: Pálvölgyi Dömötör (Budapest)

(7 pont)

statisztika

---

A. 778. Keressük meg az összes olyan $\displaystyle d$ négyzetmentes pozitív egész számot, melyre megoldható az $\displaystyle x^2+dy^2 = 2^n$ egyenlet a pozitív egész számok körében.

Javasolta: Williams Kada (Cambridge)

(7 pont)

megoldás, statisztika

---

A. 779. Adott két rögzített kör, $\displaystyle \Omega$ és a belsejében $\displaystyle \omega$. Az $\displaystyle \omega$ középpontja $\displaystyle I$. Az $\displaystyle \Omega$ körön mozog egy $\displaystyle P$ pont. A $\displaystyle P$-ből $\displaystyle \omega$-hoz húzott érintők második metszéspontja $\displaystyle \Omega$-val $\displaystyle Q$, illetve $\displaystyle R$. Az $\displaystyle IQR$ kör második metszéspontjai a $\displaystyle PI$, $\displaystyle PQ$ és $\displaystyle PR$ egyenesekkel rendre $\displaystyle J$, $\displaystyle S$, illetve $\displaystyle T$. A $\displaystyle J$ tükörképe az $\displaystyle ST$ egyenesre $\displaystyle K$. Mutassuk meg, hogy a különböző $\displaystyle PK$ egyenesek egy ponton mennek át.

(7 pont)

statisztika