A KöMaL 2020. októberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2020. november 16-án LEJÁRT. |
M. 398. Mérjük meg a gördülési ellenállási tényező értékét két különböző hengerre, kétféle talaj esetén! (A két, lehetőleg egyforma sugarú henger lehet például egy folpack fólia papírhengere és egy eredeti csomagolású alufólia-tekercs, a kétféle talaj lehet otthon a szoba padlója puha szőnyeggel és szőnyeg nélkül.) Vizsgáljuk meg, hogy mennyire tekinthető a hengerek lassulása állandónak!
Közli: Zagyva Tiborné, Baja
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2020. november 16-án LEJÁRT. |
G. 717. Egy denevér a barlang falával párhuzamosan repül 45,0 m/s sebességgel. Egy rövid ultrahang jelet bocsát ki, melynek visszhangját 0,120 s múlva hallja meg. Milyen távol repül a denevér a faltól? A barlangban az ultrahang terjedési sebessége 333 m/s.
(4 pont)
G. 718. Tegyük fel, hogy a Nap anyaga szénből és oxigénből áll. (A régi időkben komolyan felmerült ez az elképzelés.) Legfeljebb mennyi lenne a Nap teljes élettartama, ha a szén tökéletes égésekor egyenletesen ugyanannyi energiát sugározna ki időegységenként, mint jelenleg? (Számoljunk a Nap jelenlegi tömegével!)
(4 pont)
G. 719. Egy névlegesen 330 ml-es, bontatlan üdítősdoboz lebeg a vízben. Az alumíniumból készült üres doboz tömege 13 g. Hány ml gáz van a bontatlan dobozban, ha benne pontosan 330 ml üdítőital van, melynek sűrűsége jó közelítéssel megegyezik a víz sűrűségével?
(4 pont)
G. 720. A Tour de France kerékpáros körversenyen a versenyzők vízszintes terepen egyenletesen, 50 km/h sebességgel haladnak. A ,,mezőny'' és a ,,szökevények'' közötti távolság 1 km. Amikor egy enyhe, 5 km hosszú emelkedőhöz érnek, a sebességük nagyon hamar 40 km/h-ra csökken, majd az ugyancsak 5 km hosszú ereszkedőn nagyon hamar 60 km/h-ra nő. Ábrázoljuk, hogyan változik a mezőny és a szökevények közötti távolság az idő függvényében attól az időponttól kezdve, amikor a szökevények elérik az emelkedő alját!
Közli: Szabó Endre, Vágfüzes (Szlovákia)
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2020. november 16-án LEJÁRT. |
P. 5250. Egy autó állandó sebességgel halad egy hosszú, egyenes úton. A kerék egy külső pontjának ,,átlagos sebessége'' az autó haladási sebességéhez képest kisebb, nagyobb vagy egyenlő vele? Vizsgáljuk az ,,átlagos sebesség'' két különböző definícióját:
\(\displaystyle a)\) sebességvektor időátlagának nagysága;
\(\displaystyle b)\) sebességnagyság időátlaga.
Közli: Széchenyi Gábor, Budapest
(4 pont)
P. 5251. Az \(\displaystyle m\) tömegű, kis méretű testet az ábrán látható, rögzített hasáb \(\displaystyle A\) pontjában kezdősebesség nélkül elengedjük. A test a bal oldali egyenes szakaszon és az \(\displaystyle R\) sugarú köríven súrlódásmentesen csúszik. A jobb oldali egyenes szakasz nem súrlódásmentes, a súrlódási tényező \(\displaystyle \mu\).
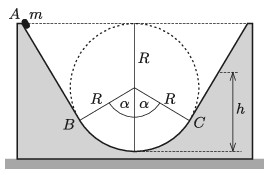
\(\displaystyle a)\) Mekkora erővel nyomja a test a hasábot a pálya legmélyebb pontján?
\(\displaystyle b)\) Mekkora a test sebessége a \(\displaystyle C\) pontban?
\(\displaystyle c)\) Milyen \(\displaystyle h\) magasságba emelkedik fel a test?
Adatok: \(\displaystyle m =0{,}6\) kg, \(\displaystyle R = 30\) cm, \(\displaystyle \alpha = 60^\circ\), \(\displaystyle \mu = \frac12 \tg\alpha\).
Közli: Kotek László, Pécs
(5 pont)
P. 5252. \(\displaystyle M\) tömegű, vékony falú csőre fonalat csévélünk, és a fonalat húzva az ábrán látható módon a csövet állandó sebességgel gurítjuk. A cső tisztán gördül a vízszintes talajon. A cső belsejébe kis méretű, \(\displaystyle m\) tömegű testet helyeztünk, ami odabent állandósult szöghelyzetben csúszik, a súrlódási együttható itt \(\displaystyle \mu\). Mekkora vízszintes fonálerő szükséges az állandó sebesség fenntartásához?
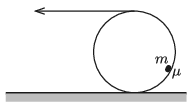
Közli: Vladár Károly, Kiskunhalas
(5 pont)
P. 5253. Az Orfűn található Pécsi-tó átlagos vízmélysége 3,3 méter. A \(\displaystyle 25\;{}^\circ\)C-os víz hőmérsékletének mekkora változása okozná a vízszint fél centiméteres süllyedését?
Közli: Simon Péter, Pécs
(4 pont)
P. 5254. Egy mól normál állapotú levegőt izotermikusan összenyomunk eredeti térfogatának felére, majd adiabatikusan kitágítjuk eredeti térfogatára.
\(\displaystyle a)\) Mekkora a folyamat során a gázon végzett összes munka?
\(\displaystyle b)\) Mennyi a gáz által leadott összes hő?
\(\displaystyle c)\) Mennyi a belső energia változása?
\(\displaystyle d)\) Mekkora a gáz végső hőmérséklete?
Példatári feladat nyomán
(4 pont)
P. 5255. Egy igen hosszú, \(\displaystyle m=10\) g tömegű, egyenes szigetelőszál középpontja felett, attól \(\displaystyle d =5\) cm-re egy \(\displaystyle Q = 3\cdot 10^{-7}\) C töltésű, pontszerű test van rögzítve. A szigetelőszálat is rögzítjük, majd egyenletes töltéseloszlással \(\displaystyle \sigma =-2\cdot 10^{-6}\) C/m lineáris töltéssűrűséggel feltöltjük. Mekkora gyorsulással indul el a szál, ha rögzítését lökésmentesen feloldjuk?
Közli: Holics László, Budapest
(5 pont)
P. 5256. Hogyan változik meg egy síkkondenzátor kapacitása, ha a fegyverzetek közötti térrész két felét két különböző dielektromos állandójú, homogén, elektromosan szigetelő anyaggal töltjük ki, és a két réteget elválasztó felület
\(\displaystyle a)\) a fegyverzetekre merőleges sík;
\(\displaystyle b)\) a fegyverzetekkel párhuzamos sík?
Közli: Wiedemann László, Budapest
(4 pont)
P. 5257. Eötvös Loránd a saját königsbergi tanáráról – Franz Ernst Neumann (1798–1895) – elnevezett fizikai törvényt az alábbi módon mutatta be. Két hosszú, egymással párhuzamosan és vízszintesen, a teremben magasan kifeszített fémhuzal végeit az egyik oldalon érzékeny galvanométerrel kötötte össze, a másik végükre egy, a huzalokra merőleges, mozgatható fémrudat helyezett. Ezután a huzalokon mint síneken végigcsúsztatta a rájuk helyezett, vízszintes fémrudat. A huzalok távolsága 2 m volt, a rúd végig a huzalokra merőleges maradt. Az akkori mérések szerint a földi mágneses térerősség iránya \(\displaystyle 62^\circ\)-os szöget zárt be a vízszintessel, a mágneses térerősség vízszintes komponensének nagyságát pedig 0,2 oerstednek mérték az akkoriban használatos CGS rendszerben.
Mekkora sebességgel húzhatta Eötvös Loránd a fémrudat akkor, amikor megállapítható volt, hogy 80 \(\displaystyle \mu\)V feszültség jutott a galvanométerre?
Közli: Radnai Gyula, Budapest
(4 pont)
P. 5258. Gyűjtőlencsével szeretnénk egy lámpa izzószáláról éles képet előállítani pontosan a lámpa alatt, az asztalon fekvő fehér lapon. Legalább hány dioptriás lencsére lesz szükségünk, ha az izzószál az asztal fölött 40 cm-re van?
Közli: Woynarovich Ferenc, Budapest
(4 pont)
P. 5259. Egy gyorsítócsőben 200 keV energiájú deuteronokból álló nyaláb érkezik a céltárgyra, az áramerősség 0,3 mA. A deuteronok lefékeződnek a céltárgyban.
\(\displaystyle a)\) Másodpercenként mennyi hőt kell elvezetni a céltárgyról, hogy az ne melegedjék?
\(\displaystyle b)\) Változik-e az eredmény, ha a deuteronok helyett ugyanekkora energiájú és ugyanekkora áramerősséget adó elektronok, illetve \(\displaystyle \alpha\)-részecskék csapódnak be a céltárgyba?
Példatári feladat nyomán
(4 pont)
P. 5260. Vízszintes tengelyű, rögzített hengeren súrlódó fonalat vetünk át. Ha a fonál bal oldali végére \(\displaystyle m\) tömegű nehezéket, a jobb oldalira pedig \(\displaystyle 3m\) tömegűt akasztunk, akkor az álló helyzetből elengedett testek 2 m/s\(\displaystyle {}^2\) nagyságú gyorsulással mozognak.
\(\displaystyle a)\) Mekkora gyorsulással mozognak a testek, ha mindkét oldalon először megduplázzuk, majd megháromszorozzuk a tömegüket?
\(\displaystyle b)\) Mekkora gyorsulással mozognak a testek, ha a jobb oldalon meghagyjuk a \(\displaystyle 3m\) nagyságú tömeget, de a bal oldali fonálvégre \(\displaystyle 8m\) tömegű testet akasztunk?
\(\displaystyle c)\) Hogyan válasszuk meg a bal oldali fonálvégre akasztott test tömegét, miközben a jobb oldalon megmarad a \(\displaystyle 3m\) tömeg, hogy elengedés után a rendszer nyugalomban maradjon?
A fonál nagyon könnyű, továbbá a fonál és a henger közötti csúszási súrlódás együtthatója megegyezik a tapadási súrlódás együtthatójával.
Közli: Honyek Gyula, Veresegyház
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)