A KöMaL 2020. decemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2021. január 15-én LEJÁRT. |
M. 400. Vizsgáljuk meg, hogy egy, a tövénél levágott fenyőág súlypontja a hosszának hányad részénél helyezkedik el! Végezzük el a mérést a levágott oldalágakra is, figyelve, hogy a fenyőágak ne nagyon hajoljanak meg! Hasonlítsuk össze a kapott eredményeket! A fenyőág lehet egy karácsonyfa legalsó ága, amelyet tőben választunk le a törzsről, mielőtt a tartólábakat felszereljük.
Közli: Horváth Norbert, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2021. január 15-én LEJÁRT. |
G. 725. A Bükkben haladó, Miskolcot Egerrel összekötő kacskaringós hegyi út kb. 50 km hosszú. Egy nyári vasárnap délelőtt mindkét irányban erős volt a forgalom. Az átlagosan 35 km/h sebességű autók mindkét irányban haladva átlagosan 1 percenként találkoztak egy-egy szembejövő gépkocsival. Becsüljük meg, hány (oda- és visszafelé haladó) autó tartózkodott egyszerre ekkor a teljes útszakaszon!
(3 pont)
G. 726. Az ábrán látható négy belső fogaskerék körbejár, a külső pedig áll. (A fogaskerekek mozgása a honlapon megtekinthető.)
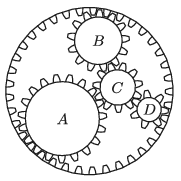
\(\displaystyle a)\) Hasonlítsuk össze a fogaskerekek keringési idejét!
\(\displaystyle b)\) Rakjuk a fogaskerekeket a középpontjuk sebessége szerint növekvő sorrendbe!
(4 pont)
G. 727. Egy vonatszerelvény 93,5 m hosszú. A vonat nyugalomból indul, és állandó gyorsulással egyenes pályán mozog. Az indulás pillanatában egy autó, amely a vonattal párhuzamosan, állandó sebességgel halad, éppen a vonat végénél van, majd 14 s múlva az autó eléri a vonat elejét. Újabb 16 s elteltével az autó megint a vonat végénél van.
\(\displaystyle a)\) Mekkora az autó sebessége?
\(\displaystyle b)\) Mekkora a vonat gyorsulása?
\(\displaystyle c)\) Mekkora utat tesz meg az autó, ameddig a vonat végleg lehagyja?
Közli: Demeter Piroska, Szeged
(3 pont)
G. 728. Vannak olyan folyadékok, például a nyers tej vagy az olívaolajos-balzsamecetes salátaöntet, melyeket ha állni hagyunk, akkor a folyadék két alkotóelemére válik szét. Az olaj kerül az öntet tetejére, illetve zsíros tejszín lesz a tej tetején, miközben a teljes térfogat nem változik. Ha az ilyen folyadékokat
\(\displaystyle a)\) felfelé keskenyedő üvegben tartjuk;
\(\displaystyle b)\) hengeres mérőpohárba töltjük;
\(\displaystyle c)\) felfelé szélesedő pohárba öntjük,
majd megvárjuk az alkotóelemek szétválását, akkor a folyadék aljánál a hidrosztatikai nyomás megnő, lecsökken vagy változatlan marad?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2021. január 15-én LEJÁRT. |
P. 5272. Az ábrán látható négy belső fogaskerék körbejár, a külső pedig áll. (A fogaskerekek mozgása a honlapon megtekinthető.)
Mekkora az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) jelű fogaskerék fordulatszáma, ha a legkisebb, \(\displaystyle D\) jelű fogaskerék másodpercenként egyszer fordul körbe?
Közli: Baranyai Klára, Veresegyház
(5 pont)
P. 5273. Az ábrán látható, vízszintes síkon elhelyezett, \(\displaystyle \alpha= 30^\circ\)-os, \(\displaystyle M = 1\) kg tömegű, \(\displaystyle h = 60\) cm magasságú derékszögű lejtő tetején nyugvó \(\displaystyle m = 0{,}5\) kg tömegű, \(\displaystyle a = 20\) cm alapú, \(\displaystyle b = 10\) cm magasságú téglatestet kezdetben nyugalomban tartjuk. Egy adott pillanatban a téglatestet elengedjük. A súrlódás mindenütt elhanyagolható.
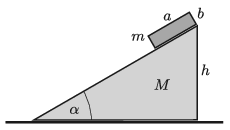
\(\displaystyle a)\) Mekkora a két test sebességének nagysága, amikor a téglatest a talajhoz ér?
\(\displaystyle b)\) Mennyi idő alatt jut el a tégla a talajhoz?
\(\displaystyle c)\) Mekkora utat tesz meg ezalatt a téglatest?
Közli: Holics László, Budapest
(5 pont)
P. 5274. Az ábrán látható, \(\displaystyle 3L\) hosszúságú, elhanyagolható tömegű, merev rúd a bal oldali végétől \(\displaystyle L\) távolságra lévő, rögzített vízszintes tengely körül súrlódásmentesen foroghat a függőleges síkban. A rúd végeihez \(\displaystyle m\), illetve \(\displaystyle 2m\) tömegű, kis méretű testeket erősítünk, és a rudat vízszintes helyzetben tartjuk. Egy adott pillanatban a rudat elengedjük.
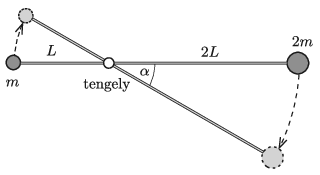
\(\displaystyle a)\) Mekkora a rúd által a tengelyre kifejtett erő rúdirányú összetevője abban a pillanatban, amikor a rúd \(\displaystyle \alpha\) szöget zár be a vízszintes iránnyal?
\(\displaystyle b)\) Határozzuk meg az \(\displaystyle \alpha\) szöget abban a pillanatban, amikor a rúd által a tengelyre kifejtett teljes erő \(\displaystyle 4mg\) nagyságú!
Közli: Kotek László, Pécs
(5 pont)
P. 5275. Az egyik kaposvári szökőkútból 1 perc alatt 1 köbméter víz szökik fel függőlegesen 5 m magasra.
\(\displaystyle a)\) Mekkora a villanymotor felvett teljesítménye, ha a szivattyúzás hatásfoka 75%?
\(\displaystyle b)\) Mekkora sebességgel áramlik ki a víz a csőből?
\(\displaystyle c)\) Mekkora a kilépő vízáram átmérője?
\(\displaystyle d)\) Mekkora a vízsugár átmérője 2,5 m magasságban?
A légellenállástól és a vízsugár cseppekre szakadásától tekintsünk el.
Közli: Gelencsér Jenő, Kaposvár
(4 pont)
P. 5276. Egy 25 cm-es átmérőre felfújt, gömb alakú lufival beszállunk Európa legnagyobb emelkedésű drótkötélpályájának kabinjába, és a hegytetőig utazunk. A kabin nem zár légmentesen, de a belső hőmérsékletét mindvégig a beszállóhely hőmérsékletén tartják. A kabin a tengerszint feletti 1000 m-es magasságból indul, és majdnem 3000 m magasba viszi fel a turistákat a Zugspitze csúcsáig. A lufin belüli nyomás mindvégig alig nagyobb a külső légnyomásnál.
Becsüljük meg, mekkora lesz a lufi átmérője, amikor kiszállunk a kabinból!
Közli: Miklós Ildikó, Tésa
(4 pont)
P. 5277. Egy fényképezőgép lencséjének fókusztávolsága 50 mm, a lencse átmérője 20 mm. A lencsét úgy állítottuk be, hogy 5 m távoli tárgyat képez le élesen. Mekkora az a legnagyobb és legkisebb távolság, amelyen belül egy pontnak a képe még kisebb, mint egy 0,05 mm átmérőjű folt a filmen? Hogyan változik ez az intervallum, ha a lencse átmérőjét leszűkítjük 10 mm-re?
Közli: Tichy Géza, Budapest
(5 pont)
P. 5278. Mennyire világítanak, ha sorba kapcsolunk és 230 V feszültségre kötünk
\(\displaystyle a)\) egy 230 V, 25 W-os izzót és egy 230 V, 100 W-os izzót;
\(\displaystyle b)\) egy 110 V, 25 W-os izzót és egy 110 V, 100 W-os izzót;
\(\displaystyle c)\) egy 110 V, 25 W-os izzót és egy 230 V, 100 W-os izzót;
\(\displaystyle d)\) egy 230 V, 25 W-os izzót és egy 110 V, 100 W-os izzót?
Közli: Honyek Gyula, Veresegyház
(4 pont)
P. 5279. Két nagyon hosszú, egymástól \(\displaystyle 2\ell\) távol lévő egyenes vezető huzal mindegyikében \(\displaystyle I\) erősségű, de ellentétes irányú áram folyik. A vezetők síkjában, az egyik vezetőtől \(\displaystyle d=\ell-b\) távolságban egy \(\displaystyle a\) és \(\displaystyle b\) oldalhosszúságú téglalap alakú vezetőkeretet helyeztünk el, először az ábrán látható 1-es, majd a 2-es helyzetben (\(\displaystyle 0<a-b<\ell)\). Melyik esetben nagyobb a kereten átmenő mágneses fluxus?
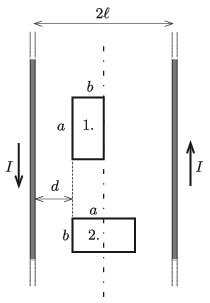
Cserti József (Budapest) feladata nyomán
(4 pont)
P. 5280. A \(\displaystyle 1{,}98~\mathrm{g/cm}^3\) sűrűségű kálium-klorid ionkristály szerkezete a kősóéval egyezik meg. Mekkora ebben a kristályban az egymáshoz legközelebb lévő pozitív és negatív ionok középpontja közötti távolság?
Közli: Radnai Gyula, Budapest
(4 pont)
P. 5281. Legfeljebb mekkora töltésre tesz szert az a szigetelőállványra rögzített, 50 mm sugarú, kezdetben töltetlen fémgömbhéj, ha hosszú ideig olyan UV lámpával világítjuk meg, melynek legalacsonyabb kisugárzott hullámhossza 280 nm? A gömbhéj anyagának kilépési munkája 3,7 eV, a levegő vezetőképességétől eltekinthetünk.
Közli: Vigh Máté, Biatorbágy
(4 pont)
P. 5282. Légpárnás asztalon mágneskorong mozog egy fémlap felett. Az örvényáramok hatására a sebességgel arányos fékezőerő hat a korongra. Egy alumíniumlap felett haladva a korong 30 cm út megtétele után áll meg, egy rézlap felett ugyanez a távolság csak 20 cm. Mekkora út megtétele után áll meg a mágneskorong, ha először egy 15 cm széles rézlap felett halad el, majd egy alumíniumlap felett folytatja mozgását? (A korong kezdősebessége mindhárom esetben ugyanakkora.)
Közli: Gnädig Péter, Vácduka
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)