A KöMaL 2020. decemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2021. január 15-én LEJÁRT. |
I. 523. András egy szabályos sokszög csúcsaiba pozitív egész számokat írt föl egymás után, az óramutató járásával azonos irányban haladva. Ezután az első csúcsnál lévő számú lépést tett a csúcsokon elindulva ettől a csúcstól az óramutató járásával ellentétes irányba. Megérkezett egy csúcshoz, majd innen kiindulva az előző iránnyal ellentétes irányba lépett a csúcsnál lévő számnak megfelelő számú lépést. Ismét megérkezett egy csúcshoz, ahonnan elindult az előző iránnyal ellentétes irányba, és ismét a csúcsnál lévő számnak megfelelő számú lépést tett. Ezt a folyamatot egészen addig folytatta, amíg egy olyan csúcsba nem ért, ahol már korábban is járt.
Készítsünk programot, amely a számsorozat alapján megadja, hogy melyik szám áll annál a csúcsnál, ahol befejeződött a folyamat.
A standard bemenet első sorában a számok N darabszáma áll (N értéke legföljebb 100), míg a második sorában N darab pozitív egész (egyik sem nagyobb 500-nál). A standard kimenet egyetlen sorába írjuk az annál a csúcsnál lévő számot, ahol befejeződött a folyamat.
Példa:

Beküldendő egy tömörített i523.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 524. Ármin bácsi és unokája, Jancsi elutazott a fáraók által építtetett piramisok megcsodálására. Az egyik piramist szeretnék megmászni, ami jó erőnlétet igényel tőlük. A piramis hatalmas faragott kőtömbökből áll, amelyek egymásra épülő szinteket alkotnak. A piramis egyik oldalán az egymást követő szinteket több párhuzamos lépcsősor is összeköti, amelyek különböző számú lépcsőt tartalmaznak. Egyik szintről a következő szintre érve a lépcsősor nem folytatódik tovább, hanem a tőle balra vagy jobbra eső új lépcsősoron lehet továbbhaladni.
A turistákat tájékoztató anyagban megtalálható, hogy a szinteket összekötő lépcsősorok hány darab lépcsőből állnak. Ármin bácsi a lassabb, így ő az összesen legtöbb lépcsőből álló útvonalat szeretné választani, míg a gyorsabb Jancsi a legkevesebből állót.
A példában az útvonalat felülről lefelé a lépcsők száma adja meg.
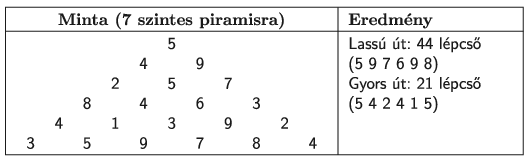
Rendelkezésünkre áll egy 15 szintből álló piramis tájékoztató anyagából a szinteket összekötő lépcsők száma a piramis.txt tabulátorral tagolt, UTF-8 kódolású állományban.
Ármin bácsi és Jancsi útvonal-kijelölését segítsük táblázatkezelővel.
1. Ármin bácsi kívánságának megfelelően számítsuk ki, hogy hány lépcsőből áll a leglassabb útvonal.
2. Adjuk meg, hogy a fürge Jancsi legkevesebb hány lépcsőfokon juthat fel a piramis tetejére.
3. Szemléltessük feltételes formázás használatával a két útvonalat.
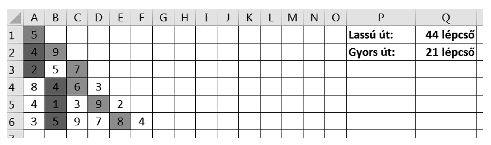
A táblázatot készítsük fel arra, hogy a piramis 15 szintje ugyan változatlan, de a lépcsők száma a szintek között a folyamatos pusztulás és renoválás következtében változhat. A megoldást hivatkozásokkal készítsük el, hogy a válasz az adatok módosításait kövesse. Segédszámításokat az R oszloptól jobbra végezhetünk, melyek értelmezését feliratokkal segítsük.
Beküldendő egy tömörített i524.zip állományban a munkafüzet, valamint egy rövid leírás, amelyben szerepel az alkalmazott táblázatkezelő neve és verziószáma.
Letölthető állomány: piramis.txt.
(10 pont)
I. 525. (É). Egy frissen alakult tanfolyamszervező cég szeretne segíteni a koronavírus miatt elbocsátott embereken, ezért igen kedvezményes áron jónéhány tanfolyamot indítana. A szervezők egy adatbázist hoztak létre a szervezés megkönnyítésére.
Az adatbázis három táblából áll:
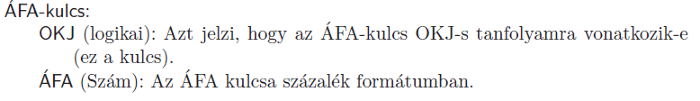

A táblák kapcsolatát ez az ábra mutatja:

Hozzunk létre i525 néven egy adatbázist.
Importáljuk az UTF-8 kódolású, a táblák nevével megegyező nevű szövegfájlokból az adatokat. Ügyeljünk a kapcsolatok megadására.
Az adattáblák tartalma egy adott napi, mondjuk január 11-ei állapotát tartalmazza az addigi jelentkezéseknek. Készítsük el az alábbi kérdésekre válaszoló lekérdezéseket, és a zárójelben adott néven mentsük őket.
1. Adjuk meg, hogy aznapig hányan jelentkeztek az egyes tanfolyamokra. (01létszámok)
2. Adjuk meg az OKJ-s tanfolyamok nevét. (02OKJ)
3. Adjuk meg, hogy melyik a két legdrágább tanfolyam. (03legdrágábbak)
4. Adjuk meg, hogy melyik a legolcsóbb OKJ-s tanfolyam. (04legolcsóbbOKJ)
5. Adjuk meg, hogy az egyes tanfolyamoknál a férőhelyek hány százalékára jelentkeztek már. (05telítettség)
6. Adjuk meg, melyik tanfolyamok teltek már be. (06betelt)
7. Azokat a tanfolyamokat a cég visszamondja, amelyekre nem jelentkezik legalább a maximális létszám fele. Adjuk meg, melyek ezek a tanfolyamok. (07lemondás)
8. Adjuk meg névsorba rendezve azon jelentkezők nevét és befizetett előlegét, akiknek a lemondás miatt vissza kell azt fizetni. (08előlegvissza)
9. Adjuk meg a cég bevételét úgy, hogy már visszafizették azok előlegét, akik tanfolyamát lemondták, és a többiek mind befizették a teljes tanfolyamdíjat. (09bevétel)
10. Számítsuk ki, hogy mennyi ÁFÁ-t kell a cégnek befizetnie a bevétele alapján. (10ÁFA)
Beküldendő egy i525.zip tömörített mappában az adatbázis, illetve egy rövid dokumentáció, amelyben szerepel a megoldáskor alkalmazott adatbázis-kezelő neve, verziószáma.
Letölthető állományok: tanfolyamok.csv, jelentkezesek.csv, AFA-kulcs.csv.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2021. január 15-én LEJÁRT. |
I/S. 49. Egy forgalmas vasútállomáson egy nagy kijelzőn tájékoztatják az utasokat az induló vonatokról. A vonatokat indulási sorrendben jelenítik meg. Minden járat egy új sorba kerül, mely tartalmazza az indulási időt, a járat azonosítóját, nevét és a vágányt, amelyikről majd indulni fog.
Nem akarják, hogy valaki a kijelzőn a járatát meglátva felszálljon egy ugyanarról a vágányról, de korábban induló vonatra. Ezért egy vonat indulásáról szóló információt addig nem jelenítik meg, amíg az összes, vele azonos vágányról korábban induló vonat el nem hagyta az állomást.
Adjuk meg minden vonatra, hogy melyik az az első időpont, amikor a vonat indulásáról szóló információ megjeleníthető. Minden vonat időben indul. Ha két vonat egyszerre hagyja el az állomást, akkor azok biztosan különböző vágányról indulnak.
Bemenet: az első sor tartalmazza a ma induló járatok N számát. Minden további sor egy-egy járatot ír le. Az első mező az indulási idő óra:perc formátumban. Utána az azonosító és a járat neve következik. Ezek az angol abc kis- és nagybetűiből állnak. A név tartalmazhat ezen felül szóközkaraktert is. Az utolsó mező a vágány v sorszáma, melyről a vonat indul.
Kimenet: N sort kell kiírni: a k-adik sor megadja a k-adik járat indulási időpontjának lehetséges legkorábbi megjelenési időpontját. Ha az adott vonat az első, amelyik a vágányt azon a napon használja, akkor a 0:00 időpontot kell kiírni.
Példa:

Korlátok: 1≤N≤105, 0≤h≤23, 0≤m≤59, 1≤v≤100. Időkorlát: 0,5 mp.
Értékelés: a pontok 40%-a kapható, ha v=1 minden sorban.
Beküldendő egy is49.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2021. január 15-én LEJÁRT. |
S. 148. Adott egy N csúcsú fa. Megkértek minket, hogy töröljük ennek a fának az egyik levelét, tehát egy olyan csúcsot, aminek pontosan egy éle van. Jelöljük ezt a levelet L-lel. A törlés után visszamarad egy N−1 csúcsú fa. Ebben az új fában jelöljük D-vel két, egymástól legmesszebb levő pont távolságát, és P-vel azon (nem rendezett) pontpárok számát, amelyek távolsága D. Adjuk meg P minimális értékét és azt, hogy ehhez hányféleképpen választhatjuk meg az L levelet (amit törlünk).
Bemenet: az első sor tartalmazza az N számot. A csúcsokat 0-tól indexeljük. A következő N−1 sor mindegyike egy x és egy y számot tartalmaz, ami azt jelenti, hogy az x-edik és y-adik csúcsot él köti össze.
Kimenet: adjuk meg P minimális értéket, és azt, hogy az hányféleképpen érhető el.
Példa:
| Bemenet (a / jel sortörést helyettesíti) | Kimenet |
| 7 / 0 1 / 1 2 / 1 3 / 3 4 / 3 5 / 5 6 | 1 2 |
Magyarázat: ha töröljük a 0-s csúcsot, akkor D=4, és a 2-es és 6-os csúcsok távolsága 4, tehát P=1. Ha töröljük a 2-es csúcsot, akkor D=4, és a 0-s és 6-os csúcsok távolsága 4, tehát P=1. Két esetben kaptunk minimális P=1-et, a többi esetben P nagyobb lesz.
Korlátok: 3≤N≤105, 0≤x,y≤N−1. Időkorlát: 0,3 mp.
Értékelés: a pontok 50%-a kapható, ha N≤100.
Beküldendő egy s148.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.
|
|

