A KöMaL 2021. februári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2021. március 16-án LEJÁRT. |
M. 402. Készítsünk vékony papírból ℓ=80 cm hosszú papírcsíkot, végeit azonos magasságban, egymástól bizonyos távolságban rögzítsük eltolható állványokon. Helyezzünk a papírcsíkra az ábrán látható helyzetben egy kis méretű, körhenger alakú, bontatlan konzervdobozt, és kezdősebesség nélkül engedjük szabadon gördülni. Mérjük meg különböző d távolságok esetén a konzervdoboz szimmetriatengelyének legnagyobb sebességét! Mekkora d-hez tartozik a maximális sebesség?
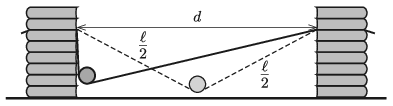
Útmutatás. A sebesség méréséhez használhatjuk pl. mobiltelefonunkat és a Tracker kiértékelő programot. (Ezen alkalmazás használatának ismeretét az emelt szintű fizika érettségin elvárják.)
Közli: Holics László, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2021. március 16-án LEJÁRT. |
G. 733. Egy kútból vizet húzunk fel. A kút mélysége 10 méter, a veder tömege 2 kg, a lánc tömege 3 kg, és a veder űrtartalma 12 liter. Mekkora a vízhúzás mechanikai hatásfoka? Függ-e a hatásfok a kút mélységétől?
Közli: Holics László, Budapest
(3 pont)
G. 734. Egy gépkocsi 3 órán át 80 km/h átlagsebességgel haladt. Három különböző útszakasz mindegyikén egyenletes sebességgel mozgott. A városi csúcsforgalomban v1=20 km/h volt a sebessége, az országúton v2=80 km/h, és végül az autópályán másfél órán keresztül v3=120 km/h sebességgel haladt. Mennyi időt töltött az autó a csúcsforgalomban, és mennyi volt az autó átlagsebessége a városi és az országúti szakaszokon együttesen?
Közli: Holics László, Budapest
(3 pont)
G. 735. Az ábrán látható hengerkerék szabadon foroghat egy rögzített tengely körül. A mozgócsigák tömege m1 és m2 (m1<m2). Milyen irányban és mekkora erővel kell húznunk a bal oldali legszélső kötélszálat, hogy a rendszer egyensúlyban legyen? (A kötél nem csúszik meg a csigákon.)
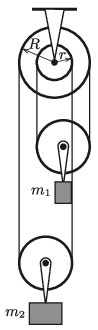
Adatok: R=10 cm, r=5 cm, m1=2 kg, m2=3 kg.
Közli: Holics László, Budapest
(4 pont)
G. 736. Egy nagy, vízzel telt tál annyira nyúlik túl az asztal szélén, hogy hajszál híján lebillen. A tál asztal fölötti részénél egy jégkocka úszik a vízen. Nagyon enyhe fuvallat lassan az asztalon kívüli rész felé sodorja a jégkockát. Mikor billen le a tál?
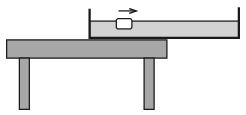
Közli: Holics László, Budapest
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2021. március 16-án LEJÁRT. |
P. 5294. Egy félhenger alakú vályú tengelye vízszintes. A vályú egyik vízszintes sugarának P felezőpontján át különböző hajlásszögű lejtőket fektetünk. Mekkora annak a lejtőnek a hajlásszöge, amelyen egy súrlódásmentesen lecsúszó piciny test leghamarabb éri el a vályú felületét?

Közli: Holics László, Budapest
(5 pont)
P. 5295. Egy LEGO-motorral hajtott m tömegű kisautó α hajlásszögű lejtőn felfelé indul el. A motor mechanikai teljesítménye (az indulás utáni nagyon rövid időtartamot leszámítva) állandó P értékű. Mekkora lesz a végsebessége? (A kerekek nem csúsznak, és a gördülő ellenállás elhanyagolhatóan kicsi.)
a) Írjuk le, milyen jellegű a kisautó mozgása!
b) Ábrázoljuk vázlatosan egy közös diagramon a teljesítményt, a sebességet, valamint a kerekekre ható tapadási súrlódási erőt az idő függvényében! Készítsük el az erő–sebesség grafikont is!
c) Mekkora a mozgás során a legkisebb súrlódási erő?
Közli: Holics László, Budapest
(5 pont)
P. 5296. Az 1∘C-os vízben egy belül üres vasgolyó lebeg. Mi történik, ha lassan emelkedik a hőmérséklet? Hány fokos vízben fog újra lebegni a vasgolyó?
Közli: Holics László, Budapest
(4 pont)
P. 5297. Egy könnyű, hajlékony, nyújthatatlan damilszál hossza ℓ=80 cm. A szál végeit azonos magasságban, egymástól valamekkora távolságban rögzítjük. A szálon egy m=5 g tömegű, közepén átfúrt acélgolyó tud csúszni. Az acélgolyót olyan helyzetből indítjuk, aminél a feszes damilszál egyik része függőleges.
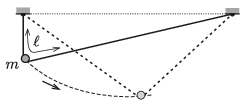
a) Legfeljebb mekkora sebességre gyorsul fel az acélgolyó, ha a súrlódás és a közegellenállás elhanyagolható?
b) Mekkora erő feszíti a damilt, amikor az acélgolyó sebessége maximális?
(Az acélgolyót tekintsük tömegpontnak!)
Holics László mérési feladata nyomán
(5 pont)
P. 5298. Két, egyenként m=0,25 kg tömegű, kis méretű acélgolyó ℓ=60 cm hosszú, nyújthatatlan fonállal van összekötve. A két golyót úgy tartjuk, hogy összekötő fonaluk vízszintes egyenes és feszültségmentes. Egy adott pillanatban a két golyót egyszerre, lökésmentesen elengedjük. h=1,8 m esés után az egyik golyó egy kiálló merev kőpárkányba ütközik. Az ütközés abszolút rugalmas.
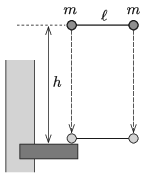
a) Mekkora erő feszíti a fonalat az ütközés utáni pillanatban?
b) Milyen magasságban lesz a párkányhoz képest az ütköző golyó az ütközés után t=14 s múlva?
(A közegellenállás elhanyagolható.)
Közli: Holics László, Budapest
(4 pont)
P. 5299. Egy vízszintes, súrlódásmentes asztalon egyenletes tömegeloszlású, M tömegű, D rugóállandójú, erős spirálrugót egyik végénél húzva F erővel gyorsítunk úgy, hogy annak minden pontja a rugó tengelyének irányában ugyanakkora gyorsulással mozog. Mekkora a rugó hossza, ha nyugalmi állapotban a hossza ℓ0≫F/D volt?
Közli: Holics László, Budapest
(4 pont)
P. 5300. Egy 10 cm átmérőjű, 20 cm gyújtótávolságú lencse optikai tengelye éppen a Nap középpontja felé mutat. A lencsétől 30 cm-re síktükröt helyezünk el az ábra szerint. Az optikai tengely mentén hova kell helyezni egy igen kicsi méretű testet, hogy a hőmérséklete a leggyorsabban emelkedjék? Tiszta napsütéses időt feltételezve mennyi idő alatt olvadna meg az ott elhelyezett kicsiny, feketére kormozott alumíniumtégelyben levő 0∘C hőmérsékletű és 0,1 cm3 térfogatú jégdarab? A lencsén, a tükrön, valamint a testeken fellépő összes energiaveszteség a hasznos energia 20%-a. A napsugárzás intenzitása a Föld felszínén 0,1 W/cm2, és a Nap képe kisebb, mint a tégely mérete.

Az optikai tengely mentén található még egy másik pont is, ahová helyezve a tégelyt a benne lévő jég hamarabb megolvad, mint a környező helyek bármelyikénél. Hol van ez a pont, és ott mennyi idő alatt olvad meg a jég?
Holics László feladata nyomán
(5 pont)
P. 5301. Pontszerű Q töltés elektromos erőterében, tőle R távolságban szabadon forgó, p momentumú, pontszerű elektromos dipólus van. Mekkora munkát kell végeznünk, ha a dipólust a rögzített töltéstől nagyon messzire (a ,,végtelenbe'') távolítjuk?
Közli: Holics László, Budapest
(4 pont)
P. 5302. Az ábrán látható alul zárt, A keresztmetszetű, felül nyitott csövet függőleges helyzetben tartjuk úgy, hogy egy m tömegű, benne könnyen csúszó, a csőből kissé kiérő tömör, nehéz dugattyút is fogunk.
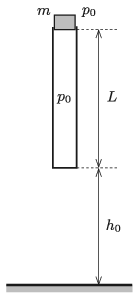
A külső p0 légnyomás és a belső nyomás kezdetben megegyezik. A bezárt légoszlop kezdeti hossza L. A cső alja a vízszintes talajtól h0 magasságra van. A külső és a kezdeti belső hőmérséklet T0. Ezt a rendszert egy adott pillanatban kezdősebesség nélkül elengedjük. A cső alja az ütközéskor hozzátapad a talajhoz. (A csőben a súrlódás, valamint a külső légkörbeli közegellenállás elhanyagolható.)
a) Mekkora lesz a maximális hőmérséklet a csőben?
b) Mekkora lesz a dugattyú legnagyobb gyorsulása?
c) Milyen magasra emelkedik a csőből kirepülő dugattyú?
Adatok: A=0,25 dm2, m=0,5 kg, p0=105 Pa, L=0,8 m, h0=0,6 m, T0=300 K.
Közli: Holics László, Budapest
(5 pont)
P. 5303. Egy puska 500 m/s sebességű lövedéke fába csapódik, és ott 5 cm-es úton lefékeződik. A lövedék tömör, 4 cm hosszú, 7800 kg/m3 sűrűségű fémhengernek tekinthető, amelynek fékeződése időben egyenletes.
a) Becsüljük meg, hogy legfeljebb mekkora mechanikai feszültség alakul ki a lövedék lefékeződése során!
b) Becsüljük meg, hogy mekkora elektromos feszültség jön létre a lövedék eleje és vége között az elektronok tehetetlensége miatt!
Holics László feladata nyomán
(5 pont)
P. 5304. Egy mozdulatlan test az Egyenlítőn helyezkedik el. Mikor kisebb a test súlya: délben vagy éjfélkor? Mekkora a test súlyának relatív megváltozása 12 óra alatt?
(A Napon és a Földön kívül más égitestek hatását ne vegyük figyelembe!)
Közli: Holics László, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

