A KöMaL 2021. februári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2021. március 16-án LEJÁRT. |
I. 529. Nevezzük rendes számoknak azokat a pozitív egészeket, amelyekben minden számjegy értéke nagyobb annál, mint ahányadik helyiértéken (balról jobbra számolva) megtalálható a számjegy. Például a 256 rendes szám, mivel az első helyen van egy 2-es, a második helyen van egy 5-ös és a harmadik helyen van egy 6-os. A 2538 viszont nem rendes szám, mert a harmadik helyen egy 3-as áll.
Készítsünk programot, amely megadja az N-edik rendes számot (1≤N≤100000). A program a standard bemenetről olvassa be N értékét, majd a standard kimenet egyetlen sorába írja ki az N-edik rendes számot.
Beküldendő egy tömörített i529.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 530. Néhány elem összes sorbarendezését, azaz ismétlés nélküli permutációját nem is olyan könnyű számítógéppel megadni.
Táblázatkezelő programban hozzuk létre az i530 nevű munkafüzetet. Ebben készítsük el az A, B, C, D, E karakterek összes lehetséges permutációját lexikografikus sorrendben az ABCDE-től az EDCBA-ig. A minta szerint számozzuk és jelenítsük meg az eseteket. Arra figyeljünk, hogy az A oszlopban csak akkor jelenjen meg szám, továbbá mellette a B oszlopban csak akkor legyen a cellának szegélye és #FFFFCC kódú héttérszíne, ha tartalmaz adatot. Az A:B tartomány adatait igazítsuk vízszintesen középre. (A mintán az 1, 2, 3, 4 számjegyek összes lehetséges sorrendjét látjuk.)
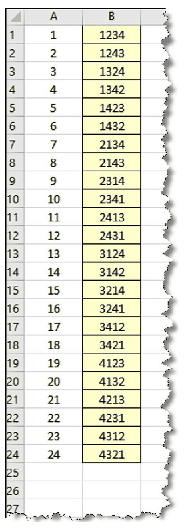
Segédszámításokat a külön erre a célra létrehozott Permutáció munkalapon végezhetünk, a Munka1 munkalapon csak az A:B tartomány tartalmazhat adatokat. A megoldáshoz makró vagy más program nem használható, csak a táblázatkezelő beépített függvényei.
Beküldendő egy i530.zip tömörített állományban a táblázatkezelő munkafüzet és egy rövid dokumentáció, amely megadja, hogy a program melyik táblázatkezelő hányas verziójában készült és egy kb. húszsoros magyarázat a megoldás módszeréről.
(10 pont)
I. 531. (É). Ebben a feladatban egy kis létszámú iskola tanulóinak adatait elemezzük adatbázis-kezelő segítségével. A tanulók adatait a tanulo.txt, az osztályok adatait pedig az osztaly.txt tabulátorral tagolt, UTF-8 kódolású szövegfájlok tartalmazzák. A mezőnevek az első sorban vannak.
Készítsünk új adatbázist i531 néven, és a mellékelt adatállományokat importáljuk az adatbázisba a forrásállományokkal azonos néven. A létrehozás során állítsuk be a megfelelő típusokat és kulcsokat.
Táblák:

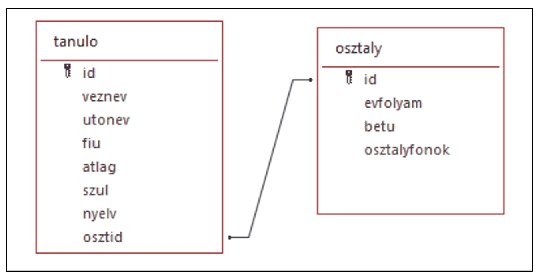
Készítsük el a következő feladatok megoldását. Az egyes lekérdezéseknél ügyeljünk arra, hogy mindig csak a kért értékek jelenjenek meg és más adatok ne. A megoldásokat a zárójelben lévő néven mentsük el.
1. Listázzuk ki a 4,5-nél jobb tanulmányi eredményt elért tanulók vezeték- és utónevét, átlagát, valamint osztályának évfolyamát és betűjelét az osztályok szerinti, azon belül pedig az átlag szerinti sorrendben. (1jelesek)
2. Írassuk ki lekérdezéssel az osztályok évfolyamát, betűjelét, létszámát és osztályátlagát. Az adatok átlag szerint csökkenő sorrendben jelenjenek meg. Az osztályátlagokat két tizedesjegyre kerekítve írassuk ki. (2osztalyok)
3. Zöld Alma szeretne nyelvi tanulmányutat szervezni a vele azonos nyelvet tanuló diákoknak. Kiket kell megkeresnie? A lekérdezésben jelenjen meg az érintett tanulók vezeték- és utóneve, valamint osztályuk évfolyama és betűjele, de maga Zöld Alma ne legyen a listában. (3alma)
4. A tanévnyitó ünnepélyen a belépő kilencedik osztályokat mindig az iskola legfiatalabb, már tavaly is ide járó tanulója köszönti. Az idén van olyan diák, aki valamennyi kilencedikesnél fiatalabb. Adjuk meg a tanuló vezeték- és utónevét, valamint évfolyamát és osztályát. Ha több ilyen tanuló is van, mindegyiket adjuk meg. (4fiatal)
5. Az iskolában az egyik legnépszerűbb idegen nyelv a francia. Ennek ellenére vannak olyan osztályok, amelyekben senki sem választotta. Az alábbi lekérdezés ezeket az osztályokat adja meg. Mit kell írnunk ehhez a … helyére? A teljes lekérdezést készítsük el. (5francia)
SELECT DISTINCT evfolyam, betu
FROM tanulo, osztaly
WHERE osztid NOT IN (...)
AND osztid=osztaly.id;
6. Az iskolában az ,,a'' osztályok reál, a ,,b'' osztályok humán tagozatosok. Igaz-e, hogy a reál tagozatos osztályokban a fiúk, a humán tagozatos osztályokban a lányok száma nagyobb? Készítsünk lekérdezést, amely kiíratja a fiúk és lányok számát mindkét tagozaton, az alábbi mintának megfelelően. (6real)
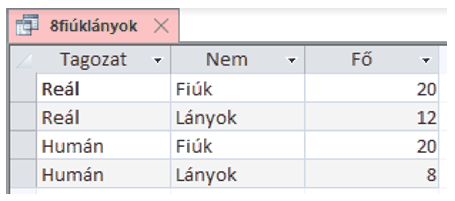
7. Határozzuk meg osztályonként a legjobb átlagú tanulókat. A lekérdezés jelenítse meg a tanulók osztályának évfolyamát és betűjelét, a tanulók vezeték- és utónevét, valamint átlagát. A lista legyen az évfolyam, azon belül osztály és a tanulók neve szerinti sorrendben. Ha egy osztályban több ilyen tanuló is van, mindegyik jelenjen meg. (7legjobbak)
8. Készítsünk jelentést, amely a mintának megfelelő szerkezetben listázza ki az iskola névsorát osztályonként. A jelentés címe és az adatok címsora a mintának megfelelően, ékezethelyesen jelenjen meg. (8Lista)

Beküldendő egy tömörített i531.zip állományban az adatbázis, valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott adatbázis-kezelő neve, verziószáma.
Letölthető állományok: tanulo.txt, osztaly.txt
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2021. március 16-án LEJÁRT. |
I/S. 51. Adott egy kép, amit egy N sorból és M oszlopból álló pixelrács reprezentál. Jelöljük az i-edik sor j-edik pixelét P[i][j]-vel. Minden pixel három különböző értéket vehet fel: R=piros, G=zöld, B=kék. A képeknél elég ritka, hogy egy P[i][j] pixel egyik élszomszédja sem azonos színű a P[i][j] pixellel, ezért ezeket gyanús pixeleknek hívjuk. Hibás pixelnek nevezzük azokat, amelyek gyanúsak, és egyik élszomszédjuk sem gyanús. Készítsünk programot, amely megadja a hibás pixelek számát.
Bemenet: az első sor tartalmazza az N és az M számot. A következő N sor mindegyike a pixelrács egy adott sorát reprezentálja. Minden sor pontosan M karakterből áll, ezek értéke lehet R, G vagy B. Az i-edik sor j-edik betűje a kép P[i][j] pixelét írja le.
Kimenet: Adjuk meg a hibás pixelek számát.
Példa:
| Bemenet (a / jel sortörést helyettesíti) | Kimenet |
| 4 4 / RRGB / RRRB / RRGG / RGRB | 1 |
Magyarázat: a P[1][3], P[4][2], P[4][3], P[4][4] pixelek gyanúsak, melyek közül csak a P[1][3] hibás.
Korlátok: 3≤N,M≤100, P[i][j]=R vagy G vagy B. Időkorlát: 0,4 mp.
Értékelés: a pontok 50%-a kapható, ha tudjuk, hogy minden gyanús pixel hibás.
Beküldendő egy is51.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2021. március 16-án LEJÁRT. |
S. 150. Van egy N×M mezőből álló játéktáblánk, melynek egyes mezői lyukasak. Van továbbá egy 1×1×2 oldalú téglatestünk, melyet a következő szabályok szerint mozgathatunk a táblán: a téglatestnek minden lépés után teljes felületével szilárd mezőn kell állnia (különben leesik); a téglatestet minden lépésben egy hosszú vagy egy rövid, a talajon lévő élén átforgatva mozgathatjuk a szomszédos mezőkre.
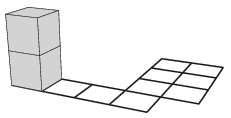
Arra vagyunk kíváncsiak, hogy el lehet-e juttatni a táblán elhelyezett téglatestet a kiinduló mezőjéről egy adott célmezőre. A téglatestnek a kiinduló és a célmezőjén is egy 1×1-es oldalán kell állnia.
Bemenet: az első sor tartalmazza a tábla sorainak és oszlopainak számát, azaz N-et és M-et. A következő N sor mindegyikében M karakter található. Az i-edik sor j-edik karaktere ,,#'', ha a mező nem lyukas, és ,,.'', ha a mező lyukas. A következő sorban a megválaszolandó kérdések Q száma szerepel. Az utána lévő Q sor mindegyikében egy téglatest kezdő mezőjének sor- és oszlopindexe, majd egy célmező sor- és oszlopindexe szerepel szóközzel elválasztva. A sorokat és oszlopokat nullától indexeljük.
Kimenet: az a szám, ahány kérdésre igen a válasz.
Példa:
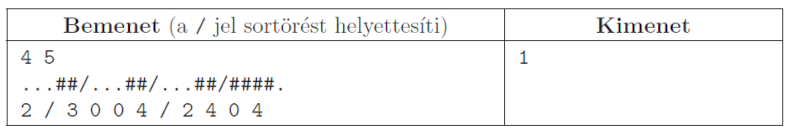
Magyarázat: az első téglatest az alábbi lépésekkel eljuthat a célba: elfektetés a (3,1) és (3,2) mezőkre, felállítás a (3,3)-ra, elfektetés az (1,3) és (2,3) mezőkre, átfordítás az (1,4)–(2,4)-re, felállítás a (0,4)-re. A második téglatest nem juttatható el a célba álló helyzetben.
Korlátok: 1≤N,M≤200, 1≤Q≤10000. Időkorlát: 0,5 mp.
Értékelés: A pontok 50%-a kapható, ha Q=1.
Beküldendő egy s150.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.
|
|

