A KöMaL 2021. májusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2021. június 15-én LEJÁRT. |
M. 405. Mérjük meg egy keverőcsaptelep vízhozamát először úgy, hogy a csapból hideg víz folyjék, majd úgy is, ha forró víz folyik a csapból! Mérjük meg a hideg és a forró víz hőmérsékletét is. Végül mérjük meg a csaptelep vízhozamát langyos víz esetében is, és számítsuk ki, hogy a langyos vízhozam hányad részét adja a hideg víz, illetve hányad részét adja a forró víz!
Közli: Honyek Gyula, Veresegyház
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2021. június 15-én LEJÁRT. |
G. 745. Milyen halmazállapotokban jelenik meg a gyertya anyaga a gyertya égésekor?
(3 pont)
G. 746. Egy madarakat szállító kamion zárt rakterében madarak üldögélnek. Amikor a jármű hangosan dudál, a madarak megijednek. Megnő, lecsökken vagy változatlan marad a kamion és a madarak együttes súlya a madarak felrebbenésekor?
(3 pont)
G. 747. Tegyük fel, hogy egy kilogramm aranyból egy atomméret vastagságú réteget hozunk létre. Becsüljük meg, hogy ezzel a réteggel hány futballpályát lehetne bevonni!
(3 pont)
G. 748. Egy magas, vízzel telt mérőhengerbe szájával lefelé fordított, 20 cm hosszú kémcsövet (Cartesius-búvárt) helyezünk úgy, hogy a kémcső felső felében levegő, alsó felében pedig víz legyen. Ekkor a kémcső úszik, zárt, felső vége kissé kiemelkedik a mérőhengerben lévő vízből. A mérőhenger tetejét gumilappal zárjuk le, majd akkora erővel nyomjuk lefelé a gumilapot, hogy ennek hatására a kémcsőben lévő levegő nyomása 5 kPa-lal megnő. Ebben a pillanatban a ,,búvár'' elindul lefelé.
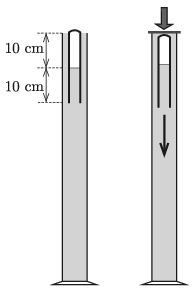
a) A ,,búvár'' elmerülésének a kezdetén mekkora volt a kémcsőbe zárt levegőoszlop magassága?
b) Legalább milyen magas a mérőhenger, ha a ,,búvár'' lent marad akkor is, amikor eltávolítjuk a gumilapot a mérőhenger tetejéről?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2021. június 15-én LEJÁRT. |
P. 5326. Egy ismeretlen magasságú toronyból elejtünk egy testet, amely szabadon esik. A közegellenállástól eltekintünk.
a) A torony magasságát gondolatban osszuk két egyenlő részre. Határozzuk meg a két egyenlő szakaszon számított átlagsebességek arányát!
b) Hogyan osszuk fel két részre a h=45 méteres torony magasságát, hogy a második szakaszon számított átlagsebesség négyszerese legyen az első szakaszon számított átlagsebességnek?
Közli: Kotek László, Pécs
(4 pont)
P. 5327. Milyen hosszú lenne egy földi nap, ha a változatlan alakú Föld saját tengelye körüli forgása miatt ,,leesnénk'' a Földről az Egyenlítőn?
Közli: Cserti József, Budapest
(3 pont)
P. 5328. Satuba fogunk vízszintesen egy könnyű, hosszú acélpálcát. A végére egy nehezéket erősítünk, ami a pálca végét 1 cm-rel nyomja le annak eredeti helyzetéhez képest. Ha kis kitérésű rezgésbe hozzuk, mennyi lesz a rezgésideje?
Közli: Gelencsér Jenő, Kaposvár
(4 pont)
P. 5329. Vízszintes táblán egy krétadarab nyugszik. A táblát meglökve, a tábla hirtelen vízszintes, v0 nagyságú sebességet kap, majd T idő múlva egy falnak ütközve ugyanilyen hirtelen megáll. Milyen hosszú nyomot hagy a kréta a táblán, ha a kréta és a tábla közötti súrlódási együttható μ?
A Kvant nyomán
(5 pont)
P. 5330. Képzeljünk el egy folyékony halmazállapotú, gömb alakú égitestet. A belső tömegvonzás hidrosztatikai nyomást eredményez. Legyen az égitest vízből, és a gömb sugara R=25 km. Mekkora a hidrosztatikai nyomás a gömb középpontjában?
Közli: Szekeres Béla, Budapest
(4 pont)
P. 5331. Régi, népi játékszer a ,,krumplilövettyű'', ami egy 12 cm hosszú, 0,3 cm2 belső keresztmetszetű bodzacső. A cső két végét egymás után egy-egy 1 cm hosszúságú krumplihengerrel dugaszoljuk el.

Az egyik krumplidugó a lövedék, a másik pedig a dugattyú szerepét tölti be. A krumplihengerek jól tömítik a csövet, egy ilyen henger megmozdításához (a tapadás legyőzéséhez) legalább 4 N erőt kell kifejtenünk. A csőben mozgó krumplidugóra 3,5 N nagyságú súrlódási erő hat. Miközben a lövedék távozik a bodzacsőből, a rá ható súrlódási erő a csőben lévő hosszával egyenesen arányosan csökken 0-ra. (A krumpli sűrűsége 1,06 g/cm3, a külső légnyomás 105 Pa.)
a) Mennyi a mindkét végén lezárt, ,,megtöltött'' állapotban lévő lövettyűben lévő levegő nyomása?
b) Egy fapálca segítségével a dugattyút lassan addig toljuk a csőben, amíg a lövedéknek szánt krumplihenger egy pukkanás kíséretében hirtelen ki nem repül. Mennyi munkát kell végeznünk a megtöltött lövettyű elsütéséhez?
c) Mekkora sebességgel hagyja el a lövedék a csövet?
Közli: Kis Tamás, Heves
(5 pont)
P. 5332. L=0,2 m hosszúságú szigetelőfonálon függ egy m tömegű, Q=1 μC töltésű golyócska. A felfüggesztés alatt 2L távolságban van egy ugyanakkora, rögzített, Q ponttöltés.
a) Hogyan függ a fonál függőlegessel bezárt szöge az m tömegtől?
b) Legalább mekkora legyen m, hogy a két golyó közti távolság L legyen?
c) Legfeljebb mekkora lehet m, hogy a két golyó közti távolság 3L legyen?
Közli: Szabó Endre, Vágfüzes (Szlovákia)
(5 pont)
P. 5333. Hengeres, 2 cm sugarú hosszú egyenes vezetékben áram folyik. A vezeték belsejében, annak tengelyétől 1,5 cm-re a mágneses indukcióvektor nagysága 2⋅10−4 T. Mekkora a mágneses indukcióvektor nagysága a vezeték tengelyétől 4 cm távolságban?
Közli: Holics László, Budapest
(4 pont)
P. 5334. A fizikai kísérletezést kedvelő Rudi születésnapjára elektronikai készletet kapott. Tüstént össze is állította az ábra szerinti kapcsolást, melyben az U=30 V feszültségű áramforrás belső ellenállása elhanyagolható, a teljesen egyforma feszültségmérők és a teljesen egyforma árammérők pedig ideálisnak tekinthetők. Az ellenállások nagysága R=50 Ω.
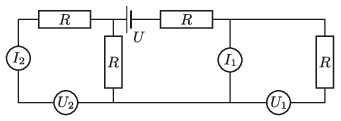
a) Mennyit mutattak a műszerek?
b) Majd megcserélte az 1-es árammérőt az 1-es feszültségmérővel, a 2-es árammérőt a 2-es feszültségmérővel. Mennyit mutattak így a műszerek?
c) Ezt követően visszarendezte a mérőműszereket az eredeti helyükre, majd az 1-es árammérőt és a 2-es feszültségmérőt felcserélte egymással. Mennyit mutattak így a műszerek?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5335. Ha tiszta 238Pu-ból készítenénk egy 8 cm átmérőjű, tömör golyót, annak felszíne hány Celsius-fok hőmérsékletre állna be, ha a −270 Celsius-fokos világűr egy mindentől távoli pontján magára hagynánk?
(Ilyen izotópot használnak a Naptól távol haladó, ,,mélyűri'' űrszondák energiaellátására a radioizotópos termoelektromos generátorokban.)
Közli: Vass Miklós, Budapest
(5 pont)
P. 5336. Elég nagy kiterjedésű, széles, sík mező fölött 2 km magasan repül egy szuperszonikus vadászgép vízszintes irányban. A gép hangját a mezőn álló három, egymástól páronként 14 km-re lévő megfigyelő egyszerre hallja meg. A repülőgép éppen az egyik megfigyelő feje felett repül el. Mekkora a vadászgép sebessége?
Közli: Vigh Máté, Biatorbágy
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

