A KöMaL 2022. januári informatika feladatai

I-jelű feladatok A beküldési határidő 2022. február 18-án LEJÁRT.

---

I. 553. Faktoriális számrendszerben a helyiértékek nem egy egész szám, az alapszám hatványai, hanem az \(\displaystyle n\)-edik helyiérték az \(\displaystyle n\) szám faktoriálisa. Tehát az első helyiértéken lévő számjegyet 1-gyel, a második helyiértéken álló számot 2-vel, a harmadik helyiértéken álló számot 6-tal kell szorozni, és így tovább. Ennek megfelelően a \(\displaystyle 3310_!\) faktoriális szám értéke tízes számrendszerben \(\displaystyle 3\cdot 4!+3\cdot 3!+1\cdot 2!=92\). Igazolható, hogy a felírás egyértelmű, tehát minden pozitív egésznek egy alakja van faktoriális számrendszerben.

Készítsünk programot i553 néven, amely egy tízes számrendszerben megadott pozitív egész számot felír faktoriális számrendszerben. A program a standard bemenet első sorából olvassa be a tízes számrendszerben felírt pozitív egészet, és a standard kimenetre írja ki a számot faktoriális számrendszerben. A bemenet legföljebb 18 számjegyből áll. Amennyiben a szám faktoriális alakjában egy helyiértéken többjegyű szám áll, akkor azt tegyük zárójelbe.

Példa bemenetek	Példa kimenetek
500	40310
5698	1052120
89764351	22732241101
1569787435467978	47068(11)0(10)725350300

Beküldendő egy tömörített i553.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika

---

I. 554. A magyar asztalitenisz-bajnokság 1905-ben kezdődött. Jelenleg ötféle versenyszám – férfi egyéni, női egyéni, férfi páros, női páros és vegyes páros – bajnoki címét osztják ki évente. A magyar nyelvű Wikipédia oldalán megtalálható adatok sok érdekes kérdés megválaszolásához nyújtanak forrást: https://hu.wikipedia.org/wiki/Magyar_asztalitenisz-bajnokság.

A feladatunk a forrásadatok feldolgozása, átrendezése olyan formába, hogy azokat adatbázisba lehessen importálni. Minden adatot a megadott webcímről mentsünk le és szervezzük az alább megadott adatbázis-szerkezetbe, más forrás nem áll rendelkezésre.

1. Mentsük le a megadott webcímről a bajnokok adatait.

Tetszőleges alkalmazással rendezzük át, töröljük ki a felesleges részeket, illetve egészítsük ki a szükséges adatokkal a táblákat. Használhatunk például szövegszerkesztőt, táblázatkezelőt vagy készíthetünk saját programot is. Az átalakítás egyes lépéseit más-más programmal is végezhetjük. A rendezett adatokat utolsó lépésként TXT típusú, tabulátorokkal tagolt UTF-8 kódolású egyszerű szöveges állományokként mentsük, amelyek neve a táblanevekkel egyezzen meg. Az állományok első sora tartalmazza a mezőneveket az adatbázisba importáláshoz.

2. A táblák kialakításához vegyük figyelembe az alábbi táblaleírásokat és kapcsolatokat:

Tábla:

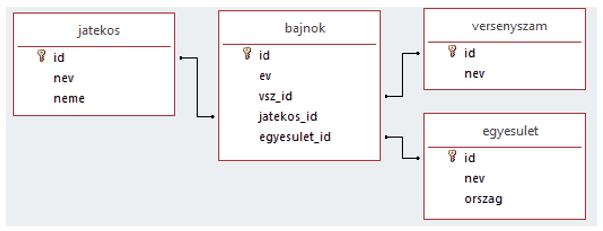
A táblák elsődleges kulcs mezőjét (id) tetszőleges értékkel kitölthetjük, míg az idegen kulcsok (jatekos_id, egyesulet_id, vsz_id mezők) megadásakor úgy járjunk el, hogy azok helyes kapcsolatot mutassanak.

Beküldendő egy tömörített i554.zip állományban a négy adattábla szöveges állománya és rövid dokumentációja, amely megadja a feldolgozás lépéseit, eszközeit.

A következő feladat a most elkészített adatbázishoz kapcsolódik. Ha megoldottuk ezt a feladatot, akkor a következő feladatban használjuk a saját megoldást az adatbázis forrásaként. Amennyiben ezt a feladatot nem vagy csak részben oldottuk meg, akkor a következő feladathoz mellékelt forrásokat használjuk annak megoldásához.

(10 pont)

megoldás, statisztika

---

I. 555. (É). A magyar asztalitenisz-bajnokság eddigi adatait kellett az I. 554. feladatban előkészíteni, azaz szöveges típusú állományokba, az adatbázisba történő importáláshoz megfelelő szerkezetben és tartalommal menteni.

Ebben a feladatban az adatbázis létrehozása, majd a kérdésekre adandó válaszokhoz lekérdezések készítése a megoldandó probléma. Az adatok, ha az I. 554. feladatot megoldottuk, akkor az ott létrehozott állományokban, vagy csökkentett rekordszámmal a jatekos.txt, a bajnok.txt, a versenyszam.txt és az egyesulet.txt állományokban állnak rendelkezésünkre. Az állományok tabulátorral tagolt, UTF-8 kódolású szövegfájlok, az első sorok a mezőneveket tartalmazzák.

A táblák kialakításához vegyük figyelembe az I. 554. feladatnál megadott táblaleírásokat és kapcsolatokat. A forrásadatok kiegészítése nem része ennek a feladatnak.

3. Készítsünk új adatbázist pingpong néven. Importáljuk az adattáblákat az adatbázisba.

4. A létrehozás során állítsuk be a megfelelő típusokat és elsődleges kulcsokat.

Készítsük el a következő feladatok megoldását. A zárójelben lévő néven mentsük el azokat. Ügyeljünk arra, hogy a megoldásban pontosan a kívánt mezők szerepeljenek.

5. Adjuk meg lekérdezés segítségével, hogy melyik évben adták ki a vegyes páros bajnoki címet először. (5vegyes)

6. Listázzuk ki lekérdezés segítségével az első 10 legtöbb bajnoki címet nyerő játékos nevét. (6top10)

7. Az egyik legeredményesebb női játékos Bátorfi Csilla volt. Lekérdezéssel adjuk meg, hogy női páros versenyszámban kikkel nyert bajnokságot. A listában minden név egyszer jelenjen meg. (7batorfiparjai)

8. Adjuk meg lekérdezés segítségével, hogy Klampár Tibor első és utolsó bajnoki címe között férfi egyesben ki szerzett még bajnoki címet. A listában minden játékos neve egyszer szerepeljen, de Klampár Tibor nevét már ne jelenítsük meg. (8klamparral)

9. Lekérdezéssel határozzuk meg, hogy a magyar egyesületeken kívül mely országok klubjainak játékosai nyertek bajnoki címet Magyarországon. Minden ország neve egyszer szerepeljen a listában. (9nemzetek)

10. Készítsünk lekérdezést, amely kilistázza azokat az éveket, amikor a női páros bajnoki címet azonos egyesülethez tartozó játékosok nyerték. A listában az évszám, a játékosok neve és az egyesületek neve jelenjen meg. (10kereszt)

Beküldendő egy tömörített i555.zip állományban a megoldást adó pingpong adatbázis és egy rövid dokumentáció, amely leírja, hogy az adatbázis melyik program segítségével készült.

Letölthető állomány: jatekos.txt, bajnok.txt, egyesulet.txt, versenyszam.txt.

(10 pont)

megoldás, statisztika

I/S-jelű feladatok A beküldési határidő 2022. február 18-án LEJÁRT.

---

I/S. 59. Egy távoli országban egy hosszas havazás után \(\displaystyle D\) gyerek eldöntötte, hogy az egész napot hóemberépítéssel fogja tölteni. A nap végére el is készítettek \(\displaystyle N\) darab hógömböt. Az \(\displaystyle i\)-edik hógömb átmérője \(\displaystyle T[i]\) milliméter. Egy hóember építésekor tetszőleges számú hógömböt kell egymás tetejére tenni (egy hóember legalább két hógömbből áll), de figyelni kell arra, hogy egy hógömbre csak egy szigorúan kisebb hógömböt tehetünk.

Egy hóember szépsége \(\displaystyle H\), ha \(\displaystyle H\) darab hógömbből áll. A gyerekek megegyeztek, hogy mindegyikük pontosan egy darab H szépségű hóembert épít a hógömbök felhasználásával. Adjuk meg azt a legnagyobb \(\displaystyle H\) szépséget, amely esetén mindegyik gyerek tud egy \(\displaystyle H\) szépségű hóembert építeni a rendelkezésre álló hógömbökből.

A bemenet első sorában az \(\displaystyle N\) és \(\displaystyle D\) számok találhatóak. A következő sor \(\displaystyle N\) darab számot tartalmaz, az \(\displaystyle i\)-edik szám \(\displaystyle T[i]\).

A kimenet egyetlen sorában egy szám szerepeljen: a legnagyobb elérhető \(\displaystyle H\) szépség. Ha nem lehetséges a megadott feltételek mellett legalább \(\displaystyle D\) azonos szépségű hóembert építeni, akkor a kimenet egyetlen sorában a \(\displaystyle -1\) szerepeljen.

Példa:

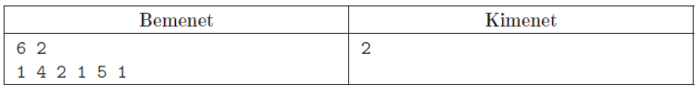
Nem építhető két darab 3 szépségű hóember, de 2 szépségű igen.

Korlátok: \(\displaystyle 1 \le N, D \le 100\,000\), \(\displaystyle 1 \le T[i] \le 10^{9}\). Időlimit: 0,4 mp.

Értékelés: a pontok 50%-a kapható, ha a program az \(\displaystyle 1 \le N \le 10\) tesztesetekre helyes megoldást ad.

Beküldendő egy is59.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

statisztika

S-jelű feladatok A beküldési határidő 2022. február 18-án LEJÁRT.

---

S. 158. Egy négyzethálón adott egy sokszög, melynek oldalai a rácsvonalakra illeszkednek. Van \(\displaystyle D\) számú dobozunk. Egy-egy dobozban 1, 2 és 3 egység hosszú pálcikák vannak, melyek összhossza megegyezik a sokszög kerületével. Kérdés, hogy le lehet-e fedni a sokszög oldalait az egyes dobozokban található pálcikákkal azok eltörése nélkül? Több pálcika alkothat egy hosszabb oldalt. Készítsünk programot, amely a sokszög és minden egyes doboz esetén megválaszolja a kérdést!

Bemenet: az első sor tartalmazza a sokszög csúcsainak \(\displaystyle N\) számát. A következő \(\displaystyle N\) sor mindegyike egy-egy csúcs \(\displaystyle x\) és \(\displaystyle y\) koordinátáját tartalmazza a sokszög valamilyen irányú körüljárása szerint. A sokszög első és utolsó csúcsa is élet alkot. A következő sorban a dobozok \(\displaystyle D\) száma van. Ezután \(\displaystyle D\) sorban az egyes dobozok tartalmát írjuk le. Ezek mindegyike három szám, melyek rendre az 1, 2, illetve 3 hosszú pálcikák darabszáma a dobozban.

Kimenet: \(\displaystyle D\) sort kell kiírni. Ezek mindegyike ,,IGEN'', ha a sokszög oldalai a doboz tartalmával lefedhetők és ,,NEM'' különben.

Példa:

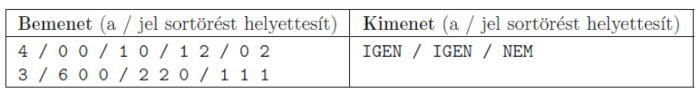
Korlátok: a koordináták abszolút értéke és a kerület is legfeljebb \(\displaystyle 10^5\). Időlimit: 1 mp.

Értékelés: a pontok 30%-a kapható, ha a program a legfeljebb 20 kerületű tesztesetekre helyes megoldást ad.

Beküldendő egy s158.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

statisztika