A KöMaL 2022. márciusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2022. április 19-én LEJÁRT. |
M. 412. Helyezzünk egymásba néhány, papírból készült muffin kosárkát, majd végezzünk ejtési kísérleteket! Mérjük meg, hogyan függ az állandósult esési sebesség a kosárkák számától! Határozzuk meg a papírkosárkák közegellenállási alaktényezőjét!
Közli: Eero Uustalu, Észtország
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2022. április 19-én LEJÁRT. |
G. 773. A Föld–Hold rendszer a két égitest közös tömegközéppontja körül kering 27,32 napos keringési idővel a távoli állócsillagokhoz képest. Ehhez képest több, mint két nappal hosszabb idő, átlagosan 29,53 nap telik el két egymást követő holdtölte között. Magyarázzuk meg a kétféle periódusidő közötti különbséget, és egyszerűsített számítással mutassuk meg, hogy valóban nagyjából két nap az eltérés!
(4 pont)
G. 774. Az alábbi diagramon a Duna felszíni sebességprofilja látható az Erzsébet-hídnál 2018. március 10-én. A vízszintes tengelyen a bal parttól mért távolság (s) látható méterben, a függőleges tengelyen a Duna sebessége (v) m/s-ban. A mellékelt táblázatban találhatóak a mért adatok.
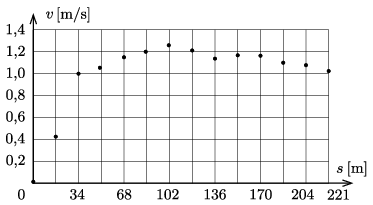
| s [m] | v [m/s] | s [m] | v [m/s] |
| 0 | 0,00 | 119 | 1,21 |
| 17 | 0,41 | 136 | 1,14 |
| 34 | 1,00 | 153 | 1,17 |
| 51 | 1,05 | 170 | 1,17 |
| 68 | 1,15 | 187 | 1,10 |
| 85 | 1,19 | 204 | 1,07 |
| 102 | 1,26 | 221 | 1,02 |
Becsüljük meg, hogy hány méterrel sodorna le a Duna, ha a bal parttól a partra mindig merőlegesen 1 m/s sebességgel eveznénk át egy, a bal parttól 221 méterre lévő hajóig!
Közli: Csernovszky Zoltán, Budapest
(4 pont)
G. 775. Elhanyagolható hőkapacitású, hőszigetelő tartályban 1 kg nagyon hideg jégkása van, amire 1 kg 100∘C-os forró vizet öntünk. Milyen hőmérsékletű volt a jégkása, ha az egyensúlyi állapotot elérve 2 liter 0∘C-os víz lesz a tartályban?
(3 pont)
G. 776. Egy kutatólaboratóriumban óraüveget szeretnének sterilizálni UV fény segítségével. A sterizáláshoz az óraüveg 1 cm2 nagyságú területére 150 mJ összenergiájú UV fénynek kell beérkeznie. Becsüljük meg, hogy mennyi ideig kell ehhez üzemeltetni az óraüveg felett 75 cm-re felszerelt (pontszerűnek tekinthető) UV-lámpát, ha a gyári adatok szerint a lámpától 1 méter távolságra az UV fény intenzitása 125 μW/cm2.
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2022. április 19-én LEJÁRT. |
P. 5391. Egy mély kútba követ ejtünk. A csobbanás hangját 4,25 s-mal az elejtés után halljuk meg. Milyen mélynek találjuk a kutat, ha g=10 m/s2-tel és vhang=320 m/s-mal számolunk? Mekkorának adódik a kút mélysége, ha g=9,81 m/s2-tel és vhang=340 m/s-mal számolunk? (A közegellenállás hatását hanyagoljuk el.)
Közli: Honyek Gyula, Veresegyház
(4 pont)
P. 5392. Egy szökőkút középső nyílásán függőlegesen kiáramló vékony vízsugár H magasságig jut el. A vízsugár ,,vízhozama'', azaz az időegységenként kiáramló víz térfogata: Φ=ΔVΔt. Milyen h magasságban lebeg egy m tömegű labda, ha a vízsugárba helyezzük? (Feltételezhetjük, hogy a vízsugár teljes keresztmetszete eléri a labdát, és arról vízszintes irányban spriccel szét.)
A Kvant nyomán
(5 pont)
P. 5393. Egy m tömegű és egy M=3m tömegű, kicsiny golyóhoz fonalakat erősítünk, melyek másik végét a bal oldali ábra szerint azonos magasságban rögzítjük. A golyók középpontja ekkor a felfüggesztés alatt L mélységben van. A kisebb tömegű golyót felemeljük úgy, hogy a hozzá kapcsolódó fonál vízszintes legyen (jobb oldali ábra), majd a golyót elengedjük. A két golyó tökéletesen rugalmasan és egyenesen ütközik.
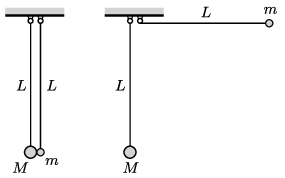
a) Az ütközés előtti pillanatban mekkora együttes erővel terheli a két fonál a felfüggesztést?
b) Mekkora a terhelés az ütközés utáni pillanatban?
c) Az első és a második ütközés között mekkora a két fonál által bezárt legnagyobb szög?
d) A c) esetben mekkora nagyságú, és milyen irányú az együttes terhelés?
e) Mekkora szöget zárnak be a fonalak a függőlegessel, amikor bekövetkezik a második ütközés?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5394. Egy m tömegű, homogén tömegeloszlású, ellipszis alakú lemez féltengelyeinek hossza a és b. Mekkora a test tehetetlenségi nyomatéka a 2a hosszúságú nagytengely végpontján átmenő, a lemez síkjára merőleges tengelyre vonatkoztatva? (A feladat elemi úton is megoldható.)
Közli: Gelencsér Jenő, Kaposvár
(5 pont)
P. 5395. Egy éve, 2021 márciusában megérkezett az első hangüzenet a Perseverance marsjárótól (go.nasa.gov/3ly2OE4). Mekkora lehet a hangsebesség a Mars légkörében?
Újsághír alapján
(4 pont)
P. 5396. Egy függőleges, hőszigetelő tartályban lévő T0 hőmérsékletű kétatomos ideális gázt szabadon mozgó hőszigetelő dugattyú zár el környezetétől. A gázt lassan melegítjük, melynek következtében térfogata növekedni kezd. Melegítés közben, amikor a gáz térfogata éppen megduplázódott, a dugattyú a hengerben található szűkítő perem miatt megakadt. Határozzuk meg a gáz végső T hőmérsékletetét, ha ismert, hogy a gázzal közölt hő 80%-a fordítódott a belső energia növelésére.
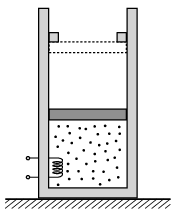
Példatári feladat nyomán
(4 pont)
P. 5397. Egy Q=10−9 C töltésű kicsiny testet egy nagy méretű, földelt fémlemeztől d=10 cm távolságban szigetelő állványon rögzítettünk.
a) Mekkora a fémlemez felületi töltéssűrűsége a kicsiny testhez legközelebb eső P pontjában?
b) Milyen messze van P-től az a pont, ahol a fémlemez felületi töltéssűrűsége a maximális értéknek egyharmada?
Közli: Holics László, Budapest
(4 pont)
P. 5398. Digitális fényképezőgépen 35 mm gyújtótávolságú objektív található, melynek közelpontja 25 cm. A közelpont az a szenzortól mért legkisebb távolság, ahonnan az objektív még képes fókuszálni.
a) Hogyan változik meg a közelpont távolsága, ha az objektív és a fényképezőgép közé egy közgyűrűt helyezünk, melynek hatására az objektív 12 mm-rel messzebbre kerül a szenzortól?
b) Készítsünk egy közelpontba helyezett tárgyról felvételt közgyűrűvel és anélkül. Hogyan aránylik egymáshoz ezen két kép nagysága?
Közli: Széchenyi Gábor, Budapest
(5 pont)
P. 5399. Egy vékony, δ vastagságú fémlemezből nagy, kúp alakú felületet hegesztettünk össze. A kúp A-val jelölt csúcsába I erősségű áramot vezetünk, majd az egyik alkotón lévő B pontból elvezetjük azt. Határozzuk meg a B-vel átellenes C pontban az áramsűrűség-vektor irányát és nagyságát! Ismert, hogy az AB távolság értéke 3R, míg a B és C pontok távolsága 2R.
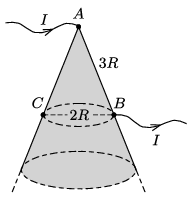
Közli: Vigh Máté, Biatorbány
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

