A KöMaL 2022. decemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2023. január 16-án LEJÁRT. |
M. 418. Mérjük meg egy labda (pl. focilabda, pingponglabda vagy teniszlabda) tehetetlenségi nyomatékát lejtőn történő legurítással! Adjuk meg az eredményt mR2 egységben is (R a labda sugara, m a tömege). Lehet-e következtetni a mérés eredményéből a labda falvastagságára?
Közli: Németh László, Fonyód
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2023. január 16-án LEJÁRT. |
G. 797. Felfújt léggömböt nyitott manométerre húzunk. A manométer két szárában a petróleum szintjének különbsége 72 cm. Hány mm lenne a szintkülönbség, ha a manométerben higany lenne? Mekkora a léggömbben uralkodó túlnyomás?
(3 pont)
G. 798. A százméteres síkfutás versenyzői térdelőrajtból indulnak. Az ábra azt mutatja, hogy mekkora vízszintes erő hat a rajtgépbe épített első és hátsó érzékelőre egy 70 kg tömegű atléta indulásakor. Becsüljük meg, hogy mekkora sebességgel hagyja el a sportoló a rajtgépet!
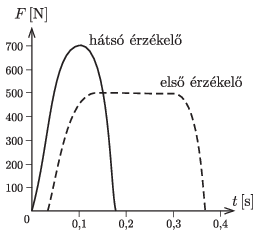
(3 pont)
G. 799. Legalább mekkora sebességgel és legfeljebb mekkora szög alatt kell indítani egy testet, hogy átrepüljön egy 100 méter hosszú, 5 méter magas, egyenes alagúton?
A légellenállás elhanyagolható.
Közli: Ringler András, Szeged
(3 pont)
G. 800. Egy gyűjtőlencse egy bizonyos helyen lévő tárgyról N1 nagyítású, valódi képet hoz létre. Ha a tárgyat az optikai tengely mentén d távolsággal messzebb visszük a lencsétől, a nagyítás N2 lesz.
Mekkora a lencse fókusztávolsága?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2023. január 16-án LEJÁRT. |
P. 5445. Egy M tömegű robbanó lövedéket α szög alatt v0 kezdősebességgel lőttek fel. Pályájának tetején a lövedék m1 és m2 tömegű részre robbant, és az m2 tömegű rész ebben a pillanatban szabadesésbe kezdett.
a) Milyen messze lesz egymástól a lövedék két darabja, amikor mindkettő talajt ért?
b) Mekkora és milyen irányú sebességgel csapódnak a talajba?
(Adatok: M=0,6 kg, m1=0,2 kg, α=60∘, v0=100 m/s. A légellenállást hanyagoljuk el.)
Közli: Holics László, Budapest
(4 pont)
P. 5446. Két diák egy mutatványra készül. A sportpályán egymástól bizonyos d távolságra lévő focilabdákat egyszerre megrúgják úgy, hogy a labdák a levegőben találkozzanak. Az egyik diák v1=20 m/s, a másik v2=10 m/s sebességgel lövi el a labdát, de a kezdősebesség irányát szabadon megválaszthatják. Legfeljebb mekkora kezdeti dmax távolságra lehet egymástól a két labda ahhoz, hogy a mutatvány sikerüljön?
(A légellenállás hatását hanyagoljuk el.)
Közli: Vigh Máté, Biatorbágy
(5 pont)
P. 5447. Három egyforma, 5 cm sugarú jéghengert készítünk, és azokat az ábrán látható helyzetből kezdősebesség nélkül elengedjük. A súrlódás mindenhol elhanyagolható.
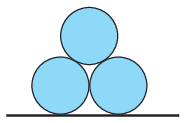
Mekkora gyorsulással indulnak el a jéghengerek?
Közli: Cserti József, Budapest
(5 pont)
P. 5448. Eduárd szerint oldalszélben (a haladási irányra pontosan merőleges szélben) körülbelül ugyanolyan nehéz biciklizni, mint szélcsendben. Az oldalszél ugyanis csak oldalra akarja nyomni a kerékpárt, ami nem lassít, legfeljebb egy kicsit bedőlve kell egyenesen is haladni, az érzékelt szembeszél pedig mindkét esetben egyforma. Vajon igaza van-e Eduárdnak?
Közli: Bodor András, Budapest
(4 pont)
P. 5449. Egy 20 cm hosszú, 3 cm\displaystyle ^2 keresztmetszetű rézrudat jó hőszigetelő köpeny vesz körül. A rudat függőlegesen tartjuk, és az egyik végét olvadó jeget tartalmazó pohárba lógatjuk; így azt folyamatosan \displaystyle 0~{}^\circ\mathrm{C} hőmérsékleten tartjuk. Hány fokra melegszik fel a rúd másik vége, ha azt egy kicsiny, 100 W teljesítményű fűtőszálas tekerccsel melegítjük? (A szükséges anyagi állandókat táblázatokban, vagy az interneten megtalálhatjuk.)
Közli: Gnädig Péter, Vácduka
(3 pont)
P. 5450. Az \displaystyle f=5 cm fókusztávolságú gyűjtőlencse optikai tengelyén, a lencsétől jobbra 30 cm-re és balra 18 cm-re található, pontszerűnek tekinthető szentjánosbogarak elkezdenek egymás felé mozogni 2 cm/s sebességgel. Mennyi idő múlva kerül fedésbe egymással a két bogár képe?
Közli: Széchenyi Gábor, Budapest
(4 pont)
P. 5451. Egy garázs váltóáramú ellátását háromfázisú betáplálással oldják meg. Ehhez öteres kábelt használnak, mind az öt ér azonos anyagú és keresztmetszetű. Az egyik vezeték (zöld-sárga) az érintésvédelmi föld, amin hibamentes használat esetén nem folyik áram. A (kék) nullvezető potenciálja mindig nulla, gyakorlatilag mindig földpotenciálon van. A három fázisvezetőben (barna, fekete és szürke) olyan módon változik a szinuszos potenciál, hogy az effektív érték \displaystyle 230 V, és bármely két fázisvezető potenciálja között \displaystyle 120^\circ-os a fáziskülönbség. Az egyes fázisvezetők és a nullvezető közé ohmos fogyasztókat kapcsolunk.
\displaystyle a) Mekkora effektív feszültséget mérhetünk két különböző fázisvezető között?
\displaystyle b) Mekkora a nullvezető effektív árama, ha két fázisvezetőben 10–10 A áram folyik, de a harmadik fázisvezetőn nem folyik áram?
\displaystyle c) Mekkora a nullvezető effektív árama, ha mind a három fázisvezetőkben 10 A áram folyik?
\displaystyle d) Mekkora a nullvezető legkisebb és legnagyobb effektív árama, ha egyik fázisvezető effektív árama se haladja meg a 10 A-es értéket?
Közli: Honyek Gyula, Veresegyház
(4 pont)
P. 5452. Egy egyenes pályán haladó fotonrakéta tömege induláskor \displaystyle m_0. Adjuk meg a rakéta sebességét a nyugalmi tömeg pillanatnyi értékének a függvényében!
(Lásd még a P. 5426. feladatot a KöMaL 2022. szeptemberi számában.)
Közli: Woynarovich Ferenc, Budapest
(4 pont)
P. 5453. Az \displaystyle r = 0{,}2 m sugarú, töltetlen fémgömb középpontjától \displaystyle d = 0{,}5 m távolságra egy \displaystyle Q nagyságú ponttöltés helyezkedik el. Határozzuk meg (akár numerikus számítással), hogy a ponttöltéstől nézve mekkora szög alatt látszanak a fémgömb azon pontjai, ahol a felületi töltéssűrűség zérus!
Közli: Szász Krisztián, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

