A KöMaL 2023. szeptemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2023. október 16-án LEJÁRT. |
M. 424. Mérjük meg, hogyan függ a hátrahúzós kisautó által megtett távolság a hátrahúzás hosszától!
Közli: Széchenyi Gábor, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2023. október 16-án LEJÁRT. |
G. 821. Tiszta, csillagfényes éjszaka észrevehetjük, hogy a csillagok ,,hunyorognak'', vagyis fényességük változik. Sőt, még a színüket is változtatják. A szabad szemmel látható bolygók viszont nem hunyorognak, nem változik a színük. Magyarázzuk meg a jelenséget! Az égbolt tetején vagy az alján hunyorognak jobban a csillagok?
(3 pont)
G. 822. Mekkora utat tesz meg a vonat, ha az állomásokon összesen 1 órát vesztegel, az állomások között 50 km/h sebességgel halad, és a teljes útra számított átlagsebessége 40 km/h?
(3 pont)
G. 823. Egy kétkarú mérleg karjait különböző hosszúságúra gyártották. Ha az egyik serpenyőbe teszünk egy sárgadinnyét, akkor 96 dekagrammal tudjuk kiegyensúlyozni. Ha a másik serpenyőbe tesszük, akkor 1,5 kilogramm tartja egyensúlyban. Mekkora a sárgadinnye tömege?
(4 pont)
G. 824. Egy \(\displaystyle \ell\) hosszúságú kígyó a hosszának feléig besiklott egy keskeny, egyenes csőbe. A kígyó kint lévő vége tetszőlegesen kanyaroghat a vízszintes talajon. Ha a kígyót homogén tömegeloszlású, \(\displaystyle \ell\) hosszúságú, hajlékony kötéllel modellezzük, akkor a sík mely pontjaiban lehet a kígyó tömegközéppontja?
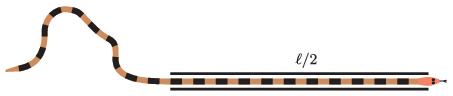
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2023. október 16-án LEJÁRT. |
P. 5499. Marci egy lejtőn csúszik le szánkójával a friss havon. Röviddel az indulását követően, egymás után négy darab szaloncukor esik ki a zsebéből (elhanyagolható magasságból) a hóra. A csúszás közben Marci a mobiltelefonja segítségével \(\displaystyle 2{,}1~\mathrm{m/s}^2\)-nek mérte a szánkó gyorsulását, és \(\displaystyle 23^\circ\)-osnak a lejtő hajlásszögét. Később a cukorkák közti távolságot is meghatározta, mely az első kettő között 2, a második és a hamadik között \(\displaystyle 3{,}2\); a harmadik és negyedik között pedig \(\displaystyle 4{,}4\) méternek adódott.
\(\displaystyle a)\) Mekkora a súrlódási együttható a szánkó és a hó között?
\(\displaystyle b)\) Igazoljuk, hogy a szaloncukrok egyenlő időközönként estek ki a fiú zsebéből!
Közli: Kis Tamás, Heves
(4 pont)
P. 5500. Egy hinta hosszú kötelei álló helyzetben legfeljebb \(\displaystyle M\) tömegű terhet bírnak el biztonságosan. Legfeljebb mekkora tömegű ember hintázhat rajta, ha a maximális kitérés egy \(\displaystyle \alpha\) hegyesszög? Eredményünket ábrázoljuk grafikonon!
Közli: Rakovszky Andorás, Budapest
(4 pont)
P. 5501. Egy kötelet helyezünk egy negyedkörív alakú, rögzített csőbe az ábrán látható módon. Mekkora sebességgel hagyja el a kötél a csövet, ha elengedjük? (A cső és a kötél közti súrlódást elhanyagolhatjuk.)
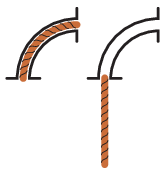
Közli: Cserti József, Budapest
(4 pont)
P. 5502. Vízben elsüllyedt teherhajó szállítmányának mentése során egy gránit szobortalapzatot emeltek ki hajódaru segítségével, egyenletes 0,2 m/s-os állandó sebességgel a 4 m mély vízből. A tömör, \(\displaystyle 2750~\mathrm{kg/m}^3\) sűrűségű gránitból álló talapzat négyzet alapú egyenes hasáb, magassága 2 m, alapéle 1,5 m, és kezdetben a folyómeder alján a négyzet alakú lapján nyugszik. A gránittömböt addig emelik, míg alsó lapja a vízfelszíntől számított 3 m magasságba kerül. Emelés közben a hosszabbik élei állandóan függőleges pozícióban maradnak.
\(\displaystyle a)\) Mennyi munkát kell végezni a teljes emelési folyamat alatt?
\(\displaystyle b)\) Hogyan változott az emelődaru teljesítménye az emelés folyamán?
Tarján Imre Országos Emlékverseny, Szolnok
(4 pont)
P. 5503. Egy \(\displaystyle V = 80~\mathrm{dm}^3\) térfogatú edényben \(\displaystyle C_V = 124{,}5~\mathrm{J/K}\) hőkapacitású, \(\displaystyle T = 402\;{}^\circ\mathrm{C}\) hőmérsékletű, \(\displaystyle p = 4{,}2\cdot 10^5\) Pa nyomású, \(\displaystyle m = 191\) g tömegű gáz van. Hány szabadsági foka van a gázrészecskéknek? Hány gázrészecske van az edényben? Milyen gáz lehet az edényben?
Közli: Holics László, Budapest
(4 pont)
P. 5504. A vízszintes síkban lévő, \(\displaystyle R\) sugarú félkör alakú vezetőben \(\displaystyle I\) erősségű áram folyik, amelyet hosszú, függőleges huzalok vezetnek a félkörbe annak végpontjainál. Az egész elrendezés függőleges irányú, \(\displaystyle \boldsymbol B\) indukcióvektorral jellemezhető homogén mágneses mezőben helyezkedik el.
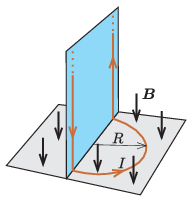
Mekkora és milyen irányú mágneses erő hat a huzalok együttesére?
Közli: Kotek László, Pécs
(4 pont)
P. 5505. Egy szobában a mennyezeten egy ötágú csillár világít, az íróasztalon egy szimmetrikus, mindkét oldalán domború kézinagyító fekszik. A nagyítóra pillantva a csillár két különböző nagyítású és tájolású képét láthatjuk.
\(\displaystyle a)\) Hogyan jön létre a két kép?
\(\displaystyle b)\) Merre állnak a csillár karjai a valóságban?
Közli: Baranyai Klára, Veresegyház
(5 pont)
P. 5506. Tekintsük az elektront kicsiny, homogén tömegeloszlású, felületén egyenletesen töltött gömbnek úgy, hogy a tömeg-energia ekvivalenciából számított energiája egyezzen meg az elektron körüli elektrosztatikus tér energiájával.
\(\displaystyle a)\) Határozzuk meg a fenti módon az elektron sugarát, amit klasszikus elektronsugárnak neveznek!
\(\displaystyle b)\) Az elektron feles spinű részecske, mert saját perdülete a \(\displaystyle \hbar\equiv h/2\pi\) redukált Planck-állandónak éppen a fele: \(\displaystyle \hbar/2\). Tekintsük az elektron saját perdületét a klasszikus newtoni mechanika alapján úgy, ahogy egy, a középpontján átmenő tengely körül forgó, homogén gömb perdületét szokás. Határozzuk meg a forgó klasszikus elektron ``egyenlítőjének'' a kerületi sebességét! Hasonlítsuk össze ezt a fénysebességgel!
Közli: Honyek Gyula, Veresegyház
(4 pont)
P. 5507. Két egyforma, érdes deszkát súrlódásmentes, vízszintes helyzetben rögzített tengely kapcsol össze. Mindkét deszka tömege \(\displaystyle m\), hossza \(\displaystyle \ell\).
A deszkák közé egy \(\displaystyle M=\frac 12 m\) tömegű, \(\displaystyle R=\frac 15 \ell\) sugarú hengert helyezünk.
\(\displaystyle a)\) Legalább mekkora kell legyen a deszkák és a henger közötti tapadási súrlódás együtthatója, hogy a henger valahol (egy alkalmasan választott helyen) egyensúlyban maradhasson?
\(\displaystyle b)\) Mekkora lehet a deszkák által bezárt szög a henger egyensúlyi állapotában?
Dózsa Márton (1914–1999) feladata nyomán
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)