A KöMaL 2023. októberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2023. november 15-én LEJÁRT. |
M. 425. Mérjük meg minél pontosabban egy talpaspohár vagy másféle üvegpohár anyagának sűrűségét!
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2023. november 15-én LEJÁRT. |
G. 825. Van egy kerek falióránk, amelynek ,,számlapján'' nincsenek számok és beosztások, csak mutatók.
A kis- és nagymutató csak a hátoldalán található gombbal állítható. Hátul kialakítottak egy körbefutó peremet, aminek segítségével az óra bármilyen helyzetben falra akasztható. A gomb megfelelő beállítása után hányféle helyzetben helyezhetjük az órát a falra úgy, hogy helyesen mutassa az időt?
Közli: Vladár Károly, Kiskunhalas
(4 pont)
G. 826. Egy autó a reggeli csúcsforgalomban fél óra hosszat halad a megengedett városi sebesség felével, majd az autópályát elérve 4 óra hosszan a megengedett legnagyobb sebesség háromnegyedével, végül 2 óra hosszat országúton a megengedett sebesség 80 százalékával mozog. Mekkora az autó átlagsebessége?
(3 pont)
G. 827. A képsorozat egy vízcsepp leszakadásának fázisait mutatja egy csöpögő csapról. Írjuk le, hogy mi történik az egyes képeken!

(4 pont)
G. 828. Tételezzük fel, hogy a Föld tökéletesen gömb alakú, tömegeloszlása gömbszimmetrikus, sugara 6400 km, tömege és tengely körüli forgásideje megegyezik az igazi Föld adataival. Egy jól megtermett fizikus az Északi-sarkon dekagramm pontos fürdőszobamérlegével éppen 100,00 kg-osnak méri magát. Mennyit mutatna ugyanez a mérleg, ha az Egyenlítőn végezné a mérést?
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2023. november 15-én LEJÁRT. |
P. 5508. Egy autó álló helyzetből indulva egyenletesen felgyorsul v0 sebességre. A gyorsítási pályaszakaszon sűrűn, egyenletes távolságokra sebességmérőket telepítettek. Mekkora a sebességmérők által mutatott értékek átlaga?
Közli: Széchenyi Gábor, Budapest
(5 pont)
P. 5509. Vízszintes talaj közelében lévő játékpuskából kilőtt kicsiny gumilövedék röppályájának emelkedési magassága megegyezik a lőtávolsággal.
a) A vízszintestől mérve milyen szögben lőttük ki a lövedéket?
b) Mekkorák ezek a távolságok, ha a test kezdősebessége 10 m/s volt?
c) Mekkora a pálya görbületi sugara a kilövés utáni pillanatban, illetve a pálya legmagasabb pontjában?
(A közegellenállást elhanyagolhatjuk.)
Közli: Holics László, Budapest
(5 pont)
P. 5510. Egy trolibusz 1 m/s2 gyorsulással indul a megállóból. Egy féllábon álló diák 1,5 m magasan kapaszkodik a menetirányban előtte lévő függőleges rúdba. Mekkora vízszintes irányú erővel húzza a 75 kg tömegű ember a rudat, hogy megtartsa függőleges testhelyzetét? Az ember súlypontja a busz padlója felett 1 m magasan van.
Közli: Honyek Gyula, Veresegyház
(4 pont)
P. 5511. Egy elhanyagolható tömegű, R sugarú abroncs egyik átmérőjének két végpontjába egy m, illetve egy M=2m tömegű, pontszerű nehezéket erősítettünk. A függőleges síkú abroncsot asztallapra helyezzük úgy, hogy kezdetben a két nehezék azonos függőleges egyenesen helyezkedik el (a nehezebb van felül). Az abroncsot ebből az instabil egyensúlyi állapotból elengedjük. Az abroncs és az asztallap közötti súrlódás elegendően nagy ahhoz, hogy az abroncs csúszásmentesen gördüljön az asztallapon.
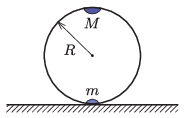
a) Mekkora az abroncs középpontjának sebessége, amikor az M tömegű nehezék eléri pályájának legalsó pontját?
b) Mekkora az a) esetben az asztalra ható nyomóerő?
Közli: Vigh Máté, Biatorbágy
(5 pont)
P. 5512. Bizonyos mennyiségű vizet egy 800 W teljesítményű merülőforralóval melegítünk fel 20∘C-ról 40∘C-ra. Azt várjuk, hogy a vizet 210 másodperc alatt tudjuk felmelegíteni, viszont ehelyett azt tapasztaljuk, hogy a melegítés 230 másodpercet vesz igénybe. Határozzuk meg az edény hőkapacitását! (Más hőveszteségtől tekintsünk el.)
Közli: Szász Krisztián, Budapest
(3 pont)
P. 5513. Két domború lencsével készíthetünk (Kepler-) távcsövet. Egy domború és egy homorú lencsével is készíthető (Galilei-) távcső. Lehet-e két homorú lencse felhasználásával távcsövet készíteni?
Tankönyvi feladat nyomán
(3 pont)
P. 5514. Vízszintes, sík felület egyik, A pontjában egy pontszerűnek tekinthető, −Q<0 töltésű test van rögzítve. A síkon egy szintén pontszerűnek tekinthető, m tömegű, q>0 töltésű test súrlódásmentesen tud mozogni. Kezdetben az m tömegű test a B pontban van, ekkor a töltések távolsága r0, és az m tömegű testnek az AB szakaszra merőlegesen, a síkkal párhuzamosan v0=√kqQmr0 nagyságú sebessége van.
(A mozgás közben a töltések nagysága nem változik.)
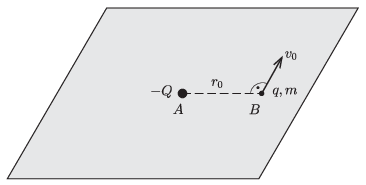
a) A mozgó test mennyi idő múlva jut ismét az AB pontok által meghatározott egyenesre?
b) Most a mozgó test kezdősebességének nagyságát felére csökkentjük. Az előbbi esetbeli időnek hányszorosa a kiindulási helytől a legtávolabbi helyig való legkorábbi eljutás ideje?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5515. A fénysebesség hányad részével mozog az elektron a Bohr-modell szerint a hidrogénatom alapállapotában?
Közli: Gnädig Péter, Vácduka
(4 pont)
P. 5516. Egy vízszintes tengely körül megpörgetett pingponglabda függőlegesen az asztallapra esik. A vékony gömbhéjnak tekinthető labda tömege m, sugara R, sebessége a leérkezéskor v0, szögsebessége ω0=v0/R, tehetetlenségi nyomatéka Θ=23mR2. A csúszási és a tapadási súrlódási együttható egyaránt μ. Tekintsük az ütközést pillanatszerűnek és tökéletesen rugalmasnak (azaz legyen a labda tömegközépponti sebességének asztalra merőleges vetülete ütközés előtt és után azonos nagyságú).
Mekkora és milyen irányú lesz a labda sebessége az ütközés után? Mekkora lesz a szögsebessége?
Közli: Balogh Péter, Gödöllő
(A nyomtatott szövegben az egyik képlet hibásan jelent meg, helyesen ω0=v0/R.)
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

