A KöMaL 2023. októberi matematika feladatai

K-jelű feladatok A beküldési határidő 2023. november 10-én LEJÁRT.

---

K. 779. Induljunk ki egy négyjegyű számból. Egy lépésben az alábbi változtatásokat hajthatjuk végre a számon:

1. Tetszőlegesen felcseréljük a számjegyeit.

2. Az első két számjegy mindegyikét növeljük 1-gyel.

A kezdő számunk legyen a 2024. Mennyi az a legkevesebb lépésszám, amellyel el tudjuk érni, hogy a számunk 7654 legyen?

(5 pont)

megoldás, statisztika

---

K. 780. $\displaystyle a)$ Két pozitív prímszám szorzatához hozzáadjuk a két prímszámot. Kaphatunk-e így prímszámot? Ha kaphatunk, adjunk rá legalább három példát, ha nem, indokoljuk meg, hogy miért nem.

$\displaystyle b)$ Két pozitív prímszám szorzatához hozzáadjuk a két prímszámot és még 1-et. Kaphatunk-e így prímszámot? Ha kaphatunk, adjunk rá legalább három példát, ha nem, indokoljuk meg, hogy miért nem.

(5 pont)

megoldás, statisztika

---

K. 781. Egy piros és egy zöld $\displaystyle 2\times3$-as táblázat mezőibe beírjuk az $\displaystyle 1$, $\displaystyle 2$, $\displaystyle 3$, $\displaystyle 4$, $\displaystyle 5$, $\displaystyle 6$ számokat úgy, hogy egy táblázaton belül minden szám pontosan egyszer szerepel. Összeadjuk a táblázatok megfelelő mezőiben álló számokat, így kapjuk a harmadik táblázatot. Az alábbiakban látunk egy példát.

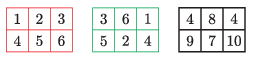
Az alábbi ábrán látható piros és zöld üres táblázatot töltsük ki úgy, hogy az összeadás után a jobb oldali táblázatot kapjuk, amelynek jobb alsó sarkát letakartuk. Adjuk meg az összes megoldást.

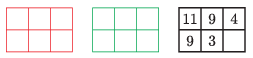
(5 pont)

megoldás, statisztika

K/C-jelű feladatok A beküldési határidő 2023. november 10-én LEJÁRT.

---

K/C. 782. Archibald rosszul emlékezett a törtek összeadásának szabályára, és így adta össze az $\displaystyle \frac ab$ és $\displaystyle \frac cd$ törteket: $\displaystyle \frac ab + \frac cd = \frac{a+c}{b+d}$. Lehetséges-e, hogy helyes végeredményt kapott, ha $\displaystyle a$, $\displaystyle b$, $\displaystyle c$, $\displaystyle d$ pozitív számok?

(5 pont)

megoldás, statisztika

---

K/C. 783. A pilóták a mutatós óra számlapjának segítségével határozzák meg az irányokat, pl. észak helyett 12 órát, kelet helyett 3 órát mondanak. Kövessük egy felderítő repülő útját, amely a földön levő bázisról nézve 1 percet repült 1 óra irányába, 2 percet 2 óra irányába, 3 percet 3 óra irányába, 10 percet 4 óra irányába, 5 percet 5 óra irányába, 6 percet 6 óra irányába, 7 percet 7 óra irányába, 8 percet 8 óra irányába, 9 percet 9 óra irányába, 4 percet 10 óra irányába, 11 percet 11 óra irányába és 12 percet 12 óra irányába. A repülő sebessége a földhöz képest végig ugyanakkora nagyságú volt. Milyen útvonalon repülhetett volna el a legrövidebb idő alatt a kiindulási helytől a célállomáshoz?

(5 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2023. november 10-én LEJÁRT.

---

C. 1778. Határozzuk meg az összes olyan $\displaystyle n$ egész számot, amelyre $\displaystyle 1+2+3+ \ldots+n$ egy azonos számjegyekből álló háromjegyű, tízes számrendszerbeli számmal egyenlő.

(Vietnami feladat)

(5 pont)

megoldás, statisztika

---

C. 1779. Igazoljuk, hogy végtelen sok olyan háromszög létezik, amelynek oldalhosszúságait a

$\displaystyle \frac{3x}{2};\quad 2x-1;\quad 3x+1$

számok adják meg, ahol $\displaystyle x$ pozitív egész. Határozzuk meg a legkisebb kerületű ilyen háromszög oldalainak hosszát.

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

C. 1780. Vannak-e olyan pozitív egész számokból álló $\displaystyle (a;b)$ rendezett párok, amelyekre az $\displaystyle a^2-2b$ és $\displaystyle b^2-2a$ is négyzetszám?

(Német versenyfeladat)

(5 pont)

megoldás, statisztika

---

C. 1781. Oldjuk meg a valós számpárok halmazán a

$$\begin{align*} 3x+\sqrt{y^2-21y} & =2x^2,\\ x^2-x-\sqrt{y^2-21y} & =x^3 \end{align*}$$

egyenletrendszert.

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

C. 1782. Az $\displaystyle ABCD$ négyzet $\displaystyle D$ csúcsából érintőt húzunk az $\displaystyle AB$ átmérőjű, a négyzet belsejébe rajzolt félkörhöz, az érintési pont (az $\displaystyle A$-tól különböző) $\displaystyle E$ pont, az $\displaystyle AB$ szakasz felezőpontja $\displaystyle F$. Az érintő a $\displaystyle BC$ egyenest a $\displaystyle G$, az $\displaystyle AB$ egyenest a $\displaystyle H$, valamint az $\displaystyle EF$ egyenes a $\displaystyle DA$ egyenest a $\displaystyle K$ pontban metszi. Bizonyítsuk be, hogy az $\displaystyle FHE$, $\displaystyle DGC$ és $\displaystyle DKE$ háromszögek beírt köreinek sugarai ebben a sorrendben egy növekvő számtani sorozat közvetlen egymás utáni tagjai.

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2023. november 10-én LEJÁRT.

---

B. 5334. Melyik az a legkisebb $\displaystyle n$, amelyre minden konvex $\displaystyle n$-szögnek van két szomszédos tompaszöge?

Erdős Pál (1913–1996) feladata

(3 pont)

megoldás, statisztika

---

B. 5335. Az $\displaystyle x$, $\displaystyle y$, $\displaystyle z$ pozitív számok szorzata 1. Mennyi lehet az

$\displaystyle \left(x+\frac{1}{x}\right)^{2} +\left(y+\frac{1}{y}\right)^{2} +\left(z+\frac{1}{z}\right)^{2} -\left(x+\frac{1}{x}\right) \left(y+\frac{1}{y}\right) \left(z+\frac{1}{z}\right)$

kifejezés értéke?

Javasolta: Kiss Géza (Csömör)

(3 pont)

megoldás, statisztika

---

B. 5336. Egy iskolai sorverseny díjazásához négyféle édességet vásároltunk. Volt közöttük $\displaystyle 1300$ Ft-os, $\displaystyle 3000$ Ft-os, $\displaystyle 3300$ Ft-os, továbbá a közönségnek feltett villámkérdések díjazásához nagyobb számban $\displaystyle 50$ Ft-os is.

Az édességekért $\displaystyle 41\,300$ Ft-ot fizettünk, az átlagár pontosan $\displaystyle 100$ Ft volt. Mennyit vettünk az egyes fajtákból?

Javasolta: Kiss Géza (Csömör)

(4 pont)

megoldás, statisztika

---

B. 5337. Egy szabályos $\displaystyle n$-szög minden oldalára megrajzoltam kifelé egy szabályos háromszöget. A háromszögek harmadik csúcsai egy nagyobb szabályos $\displaystyle n$-szöget alkotnak. Mennyi lehet $\displaystyle n$, ha a két sokszög területének aránya egész szám?

Javasolta: Hujter Bálint (Budapest)

(4 pont)

megoldás, statisztika

---

B. 5338. Egy színház nézőterének egyik sorában 10 számozott szék van. A székek a sor mindkét széléről megközelíthetők. Az egyik előadásra a sorba jegyet váltó 10 néző véletlenszerű sorrendben érkezik meg és foglalja el a helyét. A nézők nem szeretnek ,,átmászni'' az előttük megérkezett és korábban a helyét már elfoglalt többi nézőn, ezért ha tehetik, akkor a sornak annak a széléről közelítik meg a helyüket, ahonnan erre nincs szükség. Határozzuk meg annak a valószínűségét, hogy lesz legalább egy olyan néző a 10 között, aki nem tudja ,,átmászás'' nélkül elfoglalni a helyét.

Javasolta: Koncz Levente (Budapest)

(5 pont)

megoldás, statisztika

---

B. 5339. A $\displaystyle k_1$ kör belülről érinti a $\displaystyle k_2$ kört a $\displaystyle P$ pontban. Legyen $\displaystyle M$ a $\displaystyle k_1$ körvonal egy tetszőleges pontja, és messe a $\displaystyle k_1$-hez $\displaystyle M$-ben húzott érintő $\displaystyle k_2$-t az $\displaystyle A$ és $\displaystyle B$ pontokban. Mutassuk meg, hogy $\displaystyle PM$ felezi az $\displaystyle APB$ szöget.

(4 pont)

megoldás, statisztika

---

B. 5340. Legyen $\displaystyle n$ pozitív egész szám. Tegyük fel, hogy $\displaystyle f$, $\displaystyle g$ és $\displaystyle h$ legfeljebb $\displaystyle n$-edfokú, valós együtthatós polinomok. Legfeljebb hány valós $\displaystyle x$ számra lehet $\displaystyle f(x)$, $\displaystyle g(x)$, $\displaystyle h(x)$ egy nemkonstans három hosszú számtani sorozat három eleme valamilyen sorrendben, feltéve, hogy ez csak véges sok $\displaystyle x$-re teljesül?

Javasolta: Pach Péter Pál (Budapest)

(6 pont)

megoldás, statisztika

---

B. 5341. A szabályos $\displaystyle ABCD$ tetraéder súlypontja $\displaystyle S$, egy tetszőleges belső pontja $\displaystyle P$. Tükrözzük a $\displaystyle P$ pontot a tetraéder négy lapsíkjára, így kapjuk az $\displaystyle XYZW$ tetraédert. Mutassuk meg, hogy $\displaystyle XYZW$ súlypontja a $\displaystyle PS$ szakasz $\displaystyle S$-hez közelebbi harmadolópontja.

(Monthly feladat alapján)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2023. november 10-én LEJÁRT.

---

A. 860. Adott egy $\displaystyle 2^k$ darab tagból álló 0$\displaystyle \,$–$\displaystyle \,$1 sorozat. Alíz megkapja ezt a sorozatot, majd elárulhatja a sorozat egyik tagját (a tag helyét és értékét) Bobnak. Határozzuk meg azt a legnagyobb $\displaystyle s$ számot, melyre Bob biztosan tud választani $\displaystyle s$ darab tagot a sorozatból, és mindegyiknek meg tudja állapítani helyesen az értékét, akármilyen sorozatot is kapott Alíz.

Alíz és Bob a játék előtt összebeszélhetnek azzal a céllal, hogy Bob minél több jegyet biztosan meg tudjon mondani a sorozatból. Bob semmi más információt nem tud a 0$\displaystyle \,$–$\displaystyle \,$1 sorozatról a hosszán és az Alíz által választott tagon kívül.

Javasolta: Szűcs Gábor (Szikszó)

(7 pont)

megoldás, statisztika

---

A. 861. Legyen $\displaystyle f(x)=x^2-2$. Jelölje $\displaystyle f^{(n)}(x)$ a függvény $\displaystyle n$-szeres iteráltját, azaz legyen $\displaystyle f^{(1)}(x)=f(x)$ és $\displaystyle f^{(k+1)}(x)=f\big(f^{(k)}(x)\big)$.

Legyen $\displaystyle H=\big\{x\colon f^{(100)}(x)\le -1\big\}$. Határozzuk meg a $\displaystyle H$ halmaz hosszát (a $\displaystyle H$-t alkotó intervallumok hosszainak összegét). A megoldást zárt alakban várjuk.

Javasolta: Matolcsi Dávid (Budapest)

(7 pont)

megoldás, statisztika

---

A. 862. Az $\displaystyle \omega$ körbe írt $\displaystyle ABCD$ húrnégyszögben $\displaystyle F_A$, $\displaystyle F_B$, $\displaystyle F_C$ és $\displaystyle F_D$ rendre az $\displaystyle \omega$ kör $\displaystyle AB$, $\displaystyle BC$, $\displaystyle CD$, illetve $\displaystyle DA$ íveinek felezőpontja, továbbá $\displaystyle I_A$, $\displaystyle I_B$, $\displaystyle I_C$ és $\displaystyle I_D$ a $\displaystyle DAB$, $\displaystyle ABC$, $\displaystyle BCD$, illetve $\displaystyle CDA$ háromszögekbe írt kör középpontja. Legyen $\displaystyle \omega_A$ az a kör, amely az $\displaystyle F_A$ pontban belülről érinti $\displaystyle \omega$-t és érinti a $\displaystyle CD$ szakaszt, továbbá legyen $\displaystyle \omega_C$ az a kör, amely az $\displaystyle F_C$ pontban belülről érinti $\displaystyle \omega$-t és érinti az $\displaystyle AB$ szakaszt. Végül legyen $\displaystyle T_B$ az $\displaystyle \omega$ kör és az $\displaystyle F_BI_BI_C$ kör második, $\displaystyle F_B$-től különböző metszéspontja, és legyen $\displaystyle T_D$ az $\displaystyle \omega$ kör és az $\displaystyle F_DI_DI_A$ kör második, $\displaystyle F_D$-től különböző metszéspontja.

Mutassuk meg, hogy az $\displaystyle \omega_A$ és $\displaystyle \omega_C$ körök hatványvonala átmegy a $\displaystyle T_B$ és a $\displaystyle T_D$ ponton.

Javasolta: Kós Géza (Budapest)

(7 pont)

megoldás, statisztika