A KöMaL 2023. novemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2023. december 15-én LEJÁRT. |
M. 426. Mérjük meg gyári műszer használata nélkül három különböző, a háztartásban található anyag viszkozitását! Például: étolaj, méz, mosogatószer, motorolaj, tusfürdő stb.
Közli: Széchenyi Gábor, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2023. december 15-én LEJÁRT. |
G. 829. Kepler második törvénye értelmében a Napból a bolygóhoz húzott vezérsugár azonos idők alatt azonos területeket súrol. Határozzuk meg, hogy a Napból a Földhöz húzott vezérsugár másodpercenként hány \(\displaystyle \mathrm{km}^2\)-t súrol!
(3 pont)
G. 830. Egy vékony falú, 5 cm sugarú hengeres üvegedény fenéklapja kétszer vastagabb, mint a palástja. Legfeljebb milyen magas az edény, ha egy 30 fokos lejtőn a talpára állítva nem borul fel?
(A súrlódás olyan nagy, hogy az edény nem csúszik meg a lejtőn.)
(4 pont)
G. 831. Vízitúrán dobozos vaníliafagylaltot vásároltunk, melyet vékony falú, közelítőleg téglatest alakú fagylaltos dobozban árulnak. A termék címkéjéről leolvasható, hogy a töltőtömege 1250 g és a nettó térfogata 2500 ml. A doboz üresen 81 gramm tömegű, ha színültig töltjük vízzel, 2738 grammot nyom.
A lezárt, bontatlan fagylaltosdoboz úgy pottyan a vízbe, hogy a teteje néz felfelé. Becsüljük meg, hogy a magasságának hányad részéig merül a vízbe, és a magaságának hányad részéig tölti ki a fagylalt!
(4 pont)
G. 832. Egy szabályos háromszög alapú szoba kettő falát síktükör borítja. A szoba közepén áll egy lámpa. Hány képe keletkezik a lámpának?
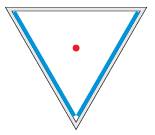
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2023. december 15-én LEJÁRT. |
P. 5517. Egy lejtő felső, \(\displaystyle \ell_1\) hosszúságú szakaszán a súrlódási együttható \(\displaystyle \mu_1\), az alsó, \(\displaystyle \ell_2\) hosszúságú szakaszán pedig \(\displaystyle \mu_2\). Egy kicsiny test nulla kezdősebességgel indulva a lejtő aljánál éppen megáll. Mekkora a lejtő hajlásszöge?
Adatok: \(\displaystyle \ell_1=20\) cm, \(\displaystyle \ell_2=40\) cm, \(\displaystyle \mu_1=0{,}1\) és \(\displaystyle \mu_2=0{,}2\).
Közli: Holics László, Budapest
(4 pont)
P. 5518. Vízszintes helyzetben rögzített, \(\displaystyle R=20\) cm sugarú, csúszós felületű hengeres testre \(\displaystyle \ell\) hosszúságú hajlékony, könnyű fonalat fektettünk az ábrán látható módon.
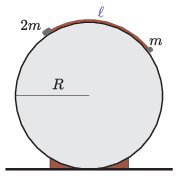
A fonál egyik végéhez \(\displaystyle m\), a másikhoz \(\displaystyle 2m\) tömegű, pontszerűnek tekinthető testet erősítettünk. Legfeljebb mekkora \(\displaystyle \ell\) esetén lehet egyensúlyban ez a rendszer?
Példatári feladat nyomán
(4 pont)
P. 5519. Dionüszosz vízszintes talajon elhelyezett egymás tetején \(\displaystyle 2\) egyforma, \(\displaystyle h\) magasságú, egyenes henger alakú, borral közel teletöltött hordót. Héraklész tizenharmadik próbájaként azt a feladatot kapja, hogy fúrjon a hordók falára merőlegesen egy-egy lyukat az alsó, illetve a felső hordóba, az adott hordó aljától mért ugyanakkora \(\displaystyle xh\) magasságban.
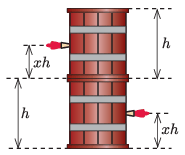
Hogyan válassza meg Héraklész a dimenziótlan \(\displaystyle x\) arányszám értékét, hogy a borsugarak földet érési pontjai a lehető legmesszebb kerüljenek egymástól?
Dürer-verseny feladata nyomán
(5 pont)
P. 5520. A mindkét végén zárt, \(\displaystyle 2\ell\) hosszúságú, vízszintesen fekvő hengert egy vékony dugattyúlap két egyenlő részre oszt. Mindkét részben \(\displaystyle 100\;{}^\circ\)C hőmérsékletű, 100 kPa nyomású levegő van. Az egyik részbe annyi vizet juttatunk, hogy telített gőz keletkezik, miközben a hőmérsékletet \(\displaystyle 100\;{}^\circ\)C-on tartjuk.
Mennyivel mozdul el a dugattyúlap és mekkora lesz mindkét részben a nyomás?
Példatári feladat
(4 pont)
P. 5521. Egy főzőlapon 12 egyforma ellenálláshuzal található, amelyek az ábrán látható módon kapcsolódnak egymáshoz.
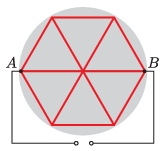
Milyen a főzőlap hőteljesítményének százalékos megoszlása az egyes huzalok között, ha az \(\displaystyle A\) és \(\displaystyle B\) pontok közé feszültséget kapcsolunk?
Közli: Tornyos Tivadar Eörs, Budapest
(4 pont)
P. 5522. Két vízszintes, párhuzamos, súrlódásmentes szigetelőrúd egymástól \(\displaystyle d\) távolságra helyezkedik el. Az alsó rúdon egy \(\displaystyle q\) töltésű, \(\displaystyle m\) tömegű, a felsőn pedig egy \(\displaystyle -q\) töltésű, \(\displaystyle m\) tömegű kicsiny szigetelőgyöngy csúszik az ábrán látható módon.
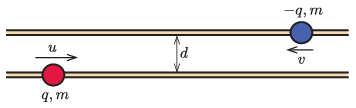
Kezdetben a gyöngyök egymástól távol helyezkednek el, és \(\displaystyle u\) illetve \(\displaystyle v\) nagyságú sebességgel indulnak egymás felé. Mekkora lesz a mozgás során az egyes testek maximális sebessége?
Közli: Németh Róbert, Budapest
(5 pont)
P. 5523. Egy szabályos hatszög alapterületű szoba három szomszédos falát síktükör borítja. A szoba közepén világít egy lámpa. Hány képe keletkezik a lámpának?
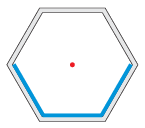
Példatári feladat nyomán
(5 pont)
P. 5524. Zárt kapilláris csőben 2 higanyoszlopot \(\displaystyle \mathrm{HgI}_2\) (higany-jodid) elektrolit vizes oldatú cseppje választ el. A cső belső átmérője 0,3 mm. A kapilláris cső a higanyhoz csatlakozó elektródákon keresztül sorba van kötve egy \(\displaystyle R=390~\mathrm{k}\Omega\)-os ellenállással és egy \(\displaystyle U=10\) V-os teleppel. Mennyi idő alatt mozdul el az oldatcsepp egy centiméternyit? Melyik irányba történik ez az elmozdulás?
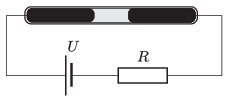
A Kvant nyomán
(4 pont)
P. 5525. Egy \(\displaystyle r\) sugarú, \(\displaystyle \varrho\) fajlagos ellenállású, hosszú, hengeres fémhuzalban \(\displaystyle I\) erősségű áram folyik egyenletes eloszlásban. A huzal felületi hőmérséklete állandó \(\displaystyle T_0\) értékű. Határozzuk meg a huzal hőmérsékletét a szimmetriatengelyén, ha ismert, hogy a fém hővezetési tényezője \(\displaystyle \lambda\)!
Közli: Vigh Máté, Biatorbágy
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)