A KöMaL 2023. decemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2024. január 15-én LEJÁRT. |
M. 427. Fizikaórán azt tanuljuk, hogy a csúszási súrlódási erő egyenesen arányos a felületeket összenyomó erővel, és az arányossági tényező nem függ a felület nagyságától. Vizsgáljuk meg (legalább kétféle anyagpárral), hogy mennyire pontosan teljesülnek ezek az állítások!
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2024. január 15-én LEJÁRT. |
G. 833. Egy gyermek minden lineáris testmérete néhány év alatt kétszeresére nő. Hogyan változik a talpai alatt a nyomás? (Feltételezhető, hogy a gyermek sűrűsége nem változik a növekedés közben.)
Közli: Simon Péter, Pécs
(3 pont)
G. 834. Megszoktuk, hogy reggel az árnyékok hosszúak, délig rövidülnek, délután nyúlnak, és alkonyatkor ismét hosszúak. Van-e olyan pontja a Földnek, ahol egy függőleges pálca vízszintes talajra vetett árnyéka egész nap ugyanolyan hosszú?
(3 pont)
G. 835. Egy autóvezető \(\displaystyle 60~\mathrm{km/h}\) sebességgel halad egy domb alján, mikor ,,üresbe'' kapcsolja az autóját. Amikor felér a domb tetejére, akkor a sebességmérője \(\displaystyle 40~\mathrm{km/h}\) értéket mutat. A közegellenállási és súrlódási veszteségeket hanyagoljuk el.
\(\displaystyle a\)) Mekkora lenne az autó sebessége a domb tetején, ha a domb aljára \(\displaystyle 70~\mathrm{km/h}\) sebességgel érkezett volna?
\(\displaystyle b\)) Mekkora minimális sebességgel haladhat az autóvezető a domb alján, hogy meghajtás nélkül feljusson annak tetejére?
Közli: Gelencsér Jenő, Kaposvár
(4 pont)
G. 836. Egy \(\displaystyle \ell=0{,}5\) m hosszú, hengeres, egyik végén zárt, a másik végén nyitott üvegcsövet nyílásával lefelé fordítva, függőleges helyzetben a Holt-tenger vizébe merítünk úgy, hogy a cső alsó (nyitott) vége \(\displaystyle h=30\) méterrel a vízfelszín alá kerül. A csőben \(\displaystyle 32\;{}^\circ\mathrm{C}\)-os hőmérsékletű és \(\displaystyle 800~\mathrm{Hgmm}\) nyomású – a légkörrel megegyező – levegő volt. A Holt-tenger vizének hőmérséklete \(\displaystyle 27\;{}^\circ\mathrm{C}\), sűrűsége a desztillált víz sűrűségének \(\displaystyle 1{,}24\)-szerese. Milyen magasra emelkedik a víz a csőben?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2024. január 15-én LEJÁRT. |
P. 5526. Álló helyzetből induló, a pályája mentén egyenletesen gyorsuló motorkerékpár mozgásának \(\displaystyle 7\). másodpercében \(\displaystyle 13~\mathrm{m}\) utat tett meg.
\(\displaystyle a)\) Mekkora utat tesz meg a \(\displaystyle 11\). másodpercben?
\(\displaystyle b)\) Mekkora a motoros gyorsulása a \(\displaystyle 11\). másodperc végén, ha a pályája \(\displaystyle 120~\mathrm{m}\) sugarú kör?
Közli: Holics László, Budapest
(4 pont)
P. 5527. Vízszintes, érdes asztalon a \(\displaystyle \mu\) csúszási súrlódási együttható az asztal peremétől mért \(\displaystyle x\) távolság függvénye. Egy kicsiny testet a peremről különböző \(\displaystyle v\) kezdősebességekkel elindítva azt tapasztaljuk, hogy a megállásig megtett út \(\displaystyle s = kv\) alakú, ahol \(\displaystyle k\) az asztalra jellemző paraméter. Határozzuk meg a súrlódási együttható helyfüggését!
Dürer Verseny feladata nyomán
(5 pont)
P. 5528. Vízszintes, súrlódásmentesnek tekinthető talajon egy \(\displaystyle d=10~\mathrm{cm}\) oldalélű, homogén tömegeloszlású kocka csúszik \(\displaystyle v_0\) sebességgel. Egyszer csak a kocka a talajhoz csatlakozó, \(\displaystyle \alpha=30^\circ\) hajlásszögű lejtőhöz ér. A lejtő és a talaj ,,törésvonala'' merőleges a kocka haladási irányára. A kocka talajjal érintkező, első oldaléle a törésvonalnál tökéletesen rugalmatlanul megakad, így a kocka megbillen. Legalább mekkora \(\displaystyle v_0\) értéke, ha a kocka elülső oldallapja ,,rábillen'' a lejtőre?
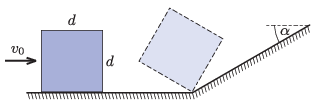
Közli: Vigh Máté, Biatorbágy
(5 pont)
P. 5529. Egy \(\displaystyle 7\) tonnás helikopter akkor tud egyhelyben lebegni, ha hajtóműve \(\displaystyle 1000~\mathrm{kW}\) teljesítményt ad le. Becsüljük meg, mekkora teljesítmény szükséges az előbbi helikopter egyhelyben lebegtetéséhez, ha az a belső terében még további \(\displaystyle 4\) tonna súlyt szállít?
Közli: Széchenyi Gábor, Budapest
(5 pont)
P. 5530. Egy orvosi fecskendő dugattyújának \(\displaystyle 300~\mathrm{mm^2}\), kivezető csöve üregének pedig \(\displaystyle 4~\mathrm{mm^2}\) a keresztmetszete. A nyitott végű eszköz dugattyújának megmozdításához (a tapadási súrlódás legyőzéséhez) \(\displaystyle 1{,}4~\mathrm{N}\) erő szükséges. Miután a kivezető csövet az ábra szerint egyik ujjunkkal befogtuk, a dugattyút egy másik ujjunkkal nagyon lassan befelé toljuk úgy, hogy egyéb helyen nem érünk a végig nyugalomban lévő fecskendőhöz (lásd az ábrát). A teljes folyamat során a bezárt levegő térfogata \(\displaystyle 20~\mathrm{cm^3}\)-ről \(\displaystyle 15~\mathrm{cm^3}\)-re csökken.
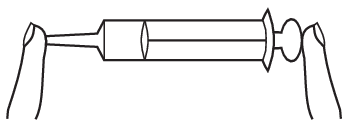
\(\displaystyle a\)) Mennyi a dugattyú betolását követően a bezárt levegő nyomása?
\(\displaystyle b\)) Legalább mekkora erővel kell szorítanunk ekkor a fecskendő kivezető csövének végét?
(A külső légnyomás \(\displaystyle 100~\mathrm{kPa}\), a fecskendő súlyától eltekinthetünk.)
Közli: Kis Tamás, Heves
(4 pont)
P. 5531. Egy Newton-féle csillagászati távcső nyitott tubusába véletlenül berepült egy világító szentjánosbogár. Amikor a tükörtől \(\displaystyle 150~\mathrm{cm}\) távol, az optikai tengelyen lévő \(\displaystyle P\) ponton keresztül az optikai tengely mentén mozgott, a képének pillanatnyi sebessége kétszer akkora volt, mint amikor a \(\displaystyle P\) ponton keresztül az előzővel megegyező sebességgel, de az optikai tengelyre merőlegesen repült. Mekkora a távcső tükrének fókusztávolsága?
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5532. Egy változtatható kapacitású kondenzátort, melynek kezdeti kapacitása \(\displaystyle C_0\), feltöltünk \(\displaystyle U_0\) feszültségre, majd egy \(\displaystyle R\) ellenálláson keresztül rövidre zárunk.
\(\displaystyle a\)) Mennyi ideig és hogyan kell a kondenzátor kapacitását változtatnunk, hogy a kondenzátor kisütése közben az áramerősség állandó maradjon?
\(\displaystyle b\)) Határozzuk meg a kondenzátor kezdeti energiájának és az ellenálláson keletkező Joule-hőnek az arányát! Adjunk magyarázatot az eredményünkre.
A Quantum Magazine nyomán
(5 pont)
P. 5533. A \(\displaystyle {}^{40}\mathrm{K}\) izotóp szokatlan viselkedésű, mert képes negatív és pozitív béta-bomlásra is, sőt elektronbefogásra is. Mekkora a háromféle folyamat bomlási energiája MeV egységben?
Útmutatás: Az izotóptömegeket lásd a https://www.komal.hu/cikkek/atomtomegek.pdf oldalon.
Példatári feladat nyomán
(4 pont)
P. 5534. Legyen egy derékszögű koordináta-rendszer \(\displaystyle x\) tengelye vízszintes, \(\displaystyle y\) tengelye pedig függőleges. Az \(\displaystyle x\) tengely \(\displaystyle 0\le \xi\le h=1~\mathrm{m}\) minden egyes \(\displaystyle x=\xi\) pontját kössük össze az \(\displaystyle y\) tengelyen lévő \(\displaystyle y=h-\xi\) ponttal. Fektessünk egy súrlódásmentes, vékony csövet az előzőek szerint felvett szakaszokból kialakuló sárga ,,síkidom'' burkolójára.
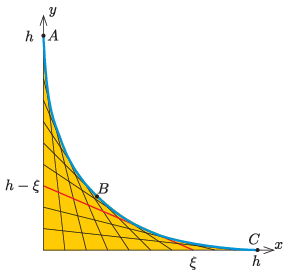
Indítsunk el lökésmentesen egy \(\displaystyle m\) tömegű, kicsiny testet a cső tetejéről. Adjuk meg \(\displaystyle mg\) egységekben, hogy a mozgása során mekkora erővel nyomja a test a cső falát
\(\displaystyle a)\) közvetlenül az indulás után az \(\displaystyle A\) pontban;
\(\displaystyle b)\) a cső \(\displaystyle B\) felezőpontjánál;
\(\displaystyle c)\) közvetlenül a cső elhagyása előtt a \(\displaystyle C\) pontnál!
Közli: Honyek Gyula, Veresegyház
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)