A KöMaL 2023. decemberi matematika feladatai

K-jelű feladatok A beküldési határidő 2024. január 10-én LEJÁRT.

K. 789. Egy számegyenesen az egész számok helyét kiszínezzük egy-egy piros vagy kék ponttal.

$\displaystyle a)$ Lehet-e úgy választani a színezést, hogy két azonos színű pont távolsága ne legyen sem 5, sem 7 egység?

$\displaystyle b)$ Lehet-e úgy választani a színezést, hogy két azonos színű pont távolsága ne legyen sem 6, sem 11 egység?

(5 pont)

megoldás, statisztika

K. 790. Bergengócia 100 leggazdagabb embere egy üzleti vacsorán találkozott egy teremben, ahol 12 hatalmas asztal állt. Akiknek a születésnapja ugyanabban a hónapban van, azok ugyanahhoz az asztalhoz ültek. Keressük meg azt az asztalt, amelyik körül a legkevesebben ültek, legyen itt $\displaystyle X$ fő. Keressük meg azt az asztalt is, ahol a legtöbben ültek, legyen itt $\displaystyle Y$ fő. Határozzuk meg $\displaystyle X$ lehető legnagyobb értékét és $\displaystyle Y$ lehető legkisebb értékét.

(5 pont)

megoldás, statisztika

K. 791. $\displaystyle a)$ Keressük meg az összes olyan háromjegyű számot, amely egyenlő számjegyei szorzatának négyszeresével.

$\displaystyle b)$ Találunk-e olyan háromjegyű számot, amely egyenlő a számjegyei szorzatának kétszeresével?

(5 pont)

megoldás, statisztika

K/C-jelű feladatok A beküldési határidő 2024. január 10-én LEJÁRT.

K/C. 792. Legyen $\displaystyle n$ pozitív egész szám. Mutassuk meg, hogy az $\displaystyle 1+2+3+ \ldots+n$ összeg utolsó számjegye nem lehet a 2, 4, 7, 9 számjegyek egyike sem.

(5 pont)

megoldás, statisztika

K/C. 793. Az ábrán szereplő $\displaystyle 3\times4$-es táblázatot kell kitöltenünk X-ekkel. A szabály az, hogy ha egy sorban vagy oszlopban pontosan két X van, akkor ezekkel egy vonalba valamelyik üres cellába beírhatunk egy harmadikat. Mutassuk meg, hogy bármilyen sorrendben is haladunk, a végén mindig marad legalább 2 üres cella.

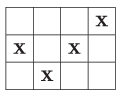
(5 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2024. január 10-én LEJÁRT.

C. 1788. Oldjuk meg az

$\displaystyle 14x^2+15y^2=7^{2023}$

egyenletet az egész számpárok halmazán.

(Svájci versenyfeladat alapján)

(5 pont)

megoldás, statisztika

C. 1789. Egy teknőc $\displaystyle 14$ egységnyi utat jár be a síkon, lépésenként egységnyi szakaszokat megtéve. Minden megtett lépést követően elfordul: ha az előző lépés sorszáma páratlan volt, akkor $\displaystyle 60^{\circ}$-kal, ha páros, akkor $\displaystyle 90^{\circ}$-kal, továbbá a $\displaystyle 3.$, $\displaystyle 5.$, $\displaystyle 8.$ és $\displaystyle 12.$ lépést követően jobbra, minden más esetben balra. Mutassuk meg, hogy a teknőc

$\displaystyle a)$ a $\displaystyle 14.$ lépés megtételével visszajut a kezdőpontjába és a kezdő irányába,

$\displaystyle b)$ adjuk meg algebrai alakban a teknőc által körüljárt területet.

Javasolta: Szilassi Lajos (Szeged)

(5 pont)

megoldás, statisztika

C. 1790. Határozzuk meg az

$\displaystyle x^2+y^2+5z^2-xy-3yz-zx+3x-4y+7z$

kifejezés legkisebb értékét, ha $\displaystyle x$, $\displaystyle y$, $\displaystyle z$ valós számok.

(Vietnámi feladat)

(5 pont)

megoldás, statisztika

C. 1791. Oldjuk meg a

$\displaystyle \frac{8^x - 15 625}{4^x + 25 \cdot 2^x + 625} = 2023$

egyenletet a valós számok halmazán.

Javasolta: Teleki Olivér (Tököl)

(5 pont)

megoldás, statisztika

C. 1792. Az $\displaystyle ABC$ háromszög $\displaystyle AB$ és $\displaystyle AC$ oldalának felezőpontja $\displaystyle F$, illetve $\displaystyle E$. Legyen $\displaystyle P$ és $\displaystyle Q$ a háromszög síkjának tetszőleges két pontja. A $\displaystyle P$ pontnak az $\displaystyle E$-re, a $\displaystyle Q$ pontnak az $\displaystyle F$-re vonatkozó tükörképe legyen $\displaystyle P'$, illetve $\displaystyle Q'$. A $\displaystyle PB$ szakasz felezőpontja $\displaystyle M$, a $\displaystyle QC$ szakasz felezőpontja $\displaystyle N$. Bizonyítsuk be, hogy $\displaystyle MN\parallel P'Q'$ és $\displaystyle P'Q'=2MN$.

Javasolta: Van Khea (Kambodzsa)

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2024. január 10-én LEJÁRT.

B. 5350. $\displaystyle a)$ Vannak-e olyan $\displaystyle a$, $\displaystyle b$, $\displaystyle c$, $\displaystyle d$ pozitív egész számok, amelyekre $\displaystyle a$ és $\displaystyle b$ számtani közepe nagyobb, mint $\displaystyle c$ és $\displaystyle d$ négyzetes közepe, de $\displaystyle a$ és $\displaystyle b$ mértani közepe kisebb, mint $\displaystyle c$ és $\displaystyle d$ harmonikus közepe?

$\displaystyle b)$ Vannak-e olyan $\displaystyle a$, $\displaystyle b$, $\displaystyle c$, $\displaystyle d$ pozitív egész számok, amelyekre $\displaystyle a$ és $\displaystyle b$ mértani közepe nagyobb, mint $\displaystyle c$ és $\displaystyle d$ négyzetes közepe, de $\displaystyle a$ és $\displaystyle b$ számtani közepe kisebb, mint $\displaystyle c$ és $\displaystyle d$ harmonikus közepe?

Javasolta: Hujter Bálint (Budapest)

(3 pont)

megoldás, statisztika

B. 5351. Az $\displaystyle ABC$ szabályos háromszög egy tetszőleges belső pontja $\displaystyle P$. Az $\displaystyle AB$-vel $\displaystyle P$-n keresztül húzott párhuzamos a $\displaystyle BC$ oldalt $\displaystyle C_1$, az $\displaystyle AC$ oldalt $\displaystyle C_2$ pontban metszi. Hasonlóan, a $\displaystyle P$-n keresztül $\displaystyle BC$-vel húzott párhuzamos az $\displaystyle AC$ oldalt $\displaystyle A_1$, az $\displaystyle AB$ oldalt $\displaystyle A_2$ pontban; végül az $\displaystyle AC$-vel húzott párhuzamos $\displaystyle AB$-t $\displaystyle B_1$, $\displaystyle BC$-t $\displaystyle B_2$ pontban metszi. Mutassuk meg, hogy az $\displaystyle A_1B_1C_1$ és $\displaystyle A_2B_2C_2$ háromszögek területe egyenlő.

Javasolta: Vígh Viktor (Sándorfalva)

(3 pont)

megoldás, statisztika

B. 5352. Milyen $\displaystyle n > 3$ egész számok esetén lehet úgy megadni $\displaystyle n$ egyenest a síkon, hogy közülük bármely három egyenlő szárú háromszöget alkosson?

Javasolta: Hujter Bálint (Budapest)

(4 pont)

megoldás, statisztika

B. 5353. Bizonyítsuk be, hogy tetszőleges 1-nél nagyobb pozitív egész $\displaystyle n$ esetén

$\displaystyle \sum_{i=1}^n\, \sum_{j=1}^n|i-j|=\frac{n(n^2-1)}{3}.$

Javasolta: Bencze Mihály (Brassó)

(4 pont)

megoldás, statisztika

B. 5354. Bizonyítsuk be, hogy egy nem egyenlő szárú háromszög Euler-egye­nese akkor és csak akkor párhuzamos a háromszög valamelyik belső szögfelezőjével, ha a felezett szög $\displaystyle 120^\circ$-os.

Javasolta: Jármai Roland (Budapest)

(5 pont)

megoldás, statisztika

B. 5355. Egy kockás füzet egy lapján $\displaystyle n$ mezőt pirosra színeztünk. A piros mezőket megszámozzuk $\displaystyle 1$-től $\displaystyle n$-ig, majd az élszomszédos piros mezőkön álló számokat összeadjuk. Igaz-e, hogy bármely $\displaystyle n$ db piros mező esetén lehet úgy számozni a piros mezőket, hogy a számpárok összeadásakor csupa különböző értéket kapjunk?

Javasolta: Imolay András (Budapest)

(5 pont)

megoldás, statisztika

B. 5356. Bizonyítsuk be, hogy tetszőleges $\displaystyle n\ge 2$ egész szám és $\displaystyle x_{1},\ldots,x_{n}$ nemnegatív valós számok esetén teljesül az alábbi egyenlőtlenség:

$\displaystyle \sqrt[\scriptstyle n]{\prod_{i=1}^{n} (1+x_{i})}\ge 1+\sqrt[\scriptstyle n]{\prod_{i=1}^{n}x_{i}}.$

Javasolta: Somogyi Ákos (London)

(6 pont)

megoldás, statisztika

B. 5357. Az $\displaystyle ABC$ háromszög körülírt köréhez $\displaystyle B$-ben és $\displaystyle C$-ben húzott érintők a $\displaystyle P$ pontban metszik egymást. Legyen a $\displaystyle PB$ és $\displaystyle AC$ egyenesek metszéspontja $\displaystyle D$, a $\displaystyle PC$ és $\displaystyle AB$ egyenesek metszéspontja $\displaystyle E$. A $\displaystyle BC$ szakaszfelező merőlegese az $\displaystyle AC$ és $\displaystyle AB$ egyeneseket rendre az $\displaystyle F$ és $\displaystyle G$ pontokban metszi. A $\displaystyle PDF$ és $\displaystyle PEG$ körök a $\displaystyle P$ ponton kívül az $\displaystyle M$ pontban metszik egymást. Legyen továbbá $\displaystyle A'$ az $\displaystyle A$ pont $\displaystyle FG$-re vonatkozó tükörképe, és $\displaystyle O$ az $\displaystyle AFG$ kör középpontja. Mutassuk meg, hogy az $\displaystyle OA'$ egyenes, és az $\displaystyle MFG$ és $\displaystyle ADE$ körök egy közös pontra illeszkednek.

Javasolta: Baris Koyuncu (Isztambul)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2024. január 10-én LEJÁRT.

A. 866. Egy gráfot kétszeresen összefüggőnek nevezünk, ha bármelyik csúcsát (és a hozzá tartozó éleket) elvéve a gráf összefüggő marad.

Igaz-e, hogy minden kétszeresen összefüggő, megszámlálhatóan végtelen sok pontból álló gráfban lehet találni olyan, az egyik irányban végtelen sétát (azaz nem feltétlenül különböző csúcsok olyan $\displaystyle v_1, v_2,\ldots$ sorozatát, melyekre $\displaystyle v_i$ és $\displaystyle v_{i+1}$ között mindig van él), amely minden élen legfeljebb egyszer megy át?

Javasolta: Bursics Balázs és Kocsis Anett (Budapest)

(7 pont)

megoldás, statisztika

A. 867. Legyen $\displaystyle p(x)$ egy $\displaystyle n$-edfokú, 1 főegyütthatójú, egész együtthatós polinom, melynek $\displaystyle n$ darab valós gyöke van: $\displaystyle \alpha_1, \alpha_2,\ldots, \alpha_n$. Legyen $\displaystyle q(x)$ egy tetszőleges egész együtthatós polinom, amely relatív prím a $\displaystyle p(x)$ polinomhoz (azaz nincs olyan nem konstans 1 vagy $\displaystyle -1$, egész együtthatós polinom, mely $\displaystyle p(x)$-et és $\displaystyle q(x)$-et is osztja). Bizonyítsuk be, hogy

$\displaystyle \sum_{i=1}^{n} \big|q(\alpha_i)\big|\ge n.$

Javasolta: Matolcsi Dávid (Berkeley)

(7 pont)

megoldás, statisztika

A. 868. Egy síkbeli ponthalmazt diszharmonikusnak nevezünk, ha bármely két, a pontok által meghatározott távolság aránya vagy $\displaystyle 100/101$ és $\displaystyle 101/100$ közé esik, vagy pedig legalább 100 vagy legfeljebb $\displaystyle 1/100$.

Igaz-e, hogy tetszőleges síkbeli, különböző $\displaystyle A_1, A_2,\ldots, A_n$ pontok esetén lehet találni olyan $\displaystyle A'_1, A'_2,\ldots,A'_n$ pontokat, melyek diszharmonikus ponthalmazt alkotnak, továbbá $\displaystyle A_i$, $\displaystyle A_j$ és $\displaystyle A_k$ pontosan akkor esnek ebben a sorrendben egy egyenesre, ha $\displaystyle A'_i$, $\displaystyle A'_j$ és $\displaystyle A'_k$ ebben a sorrendben egy egyenesre esnek (minden különböző $\displaystyle 1\le i,j,k\le n$ számhármas esetén).

Javasolta: Pálvölgyi Dömötör és Keszegh Balázs (Budapest)

(7 pont)

megoldás, statisztika