A KöMaL 2024. januári fizika feladatai

M-jelű feladatok A beküldési határidő 2024. február 15-én LEJÁRT.

---

M. 428. Mérjük meg, mekkora teljesítménnyel lehet vizet melegíteni egy mikrohullámú sütővel! Mitől függhet ez az érték?

Közli: Széchenyi Gábor, Budapest

(6 pont)

statisztika

G-jelű feladatok A beküldési határidő 2024. február 15-én LEJÁRT.

---

G. 837. Tekintsük $\displaystyle 100~{}\kern-.4pt^\circ\kern-.4pt\text{C}$-on és normál légköri nyomáson a víz folyékony és gáz halmazállapotú fázisát. Átlagosan hányszor messzebb van a szomszédos vízmolekulák középpontja egymástól a gőzfázisban, mint a folyadékfázisban?

(3 pont)

megoldás, statisztika

---

G. 838. Az alábbi, drónról készült fényképen vízszintes talajon emberek haladnak a Rio Grande partján Mexikó és az Egyesült Államok határán. Becsüljük meg, hogy milyen magasan volt a Nap a fotó készítésekor!

(4 pont)

megoldás, statisztika

---

G. 839. Két motoros halad egymás mögött $\displaystyle 30~\text{m}/\text{s}$ sebességgel egy versenypályán, a közöttük lévő távolság $\displaystyle 23~\text{m}$, a motorkerékpárok hossza $\displaystyle 2~\text{m}$. Egyszer csak a hátsó motoros előzésbe kezd, $\displaystyle 1~\text{m}/\text{s}^2$-tel gyorsít addig, míg $\displaystyle 23~\text{m}$-rel a társa elé nem kerül, majd állandó sebességgel halad tovább. Abban a pillanatban, amikor befejezi az előzést, a másik motoros is előzésbe kezd szintén $\displaystyle 1~\text{m}/\text{s}^2$-es gyorsulással, amit hasonlóan $\displaystyle 23~\text{m}$-rel a társa előtt fejez be. Mekkora sebességet érnek el a motorosok a kétszeres előzés után?

(4 pont)

megoldás, statisztika

---

G. 840. Legalább mekkora sebességgel csapódjon a falnak egy szobahőmérsékletű ólomgolyó, hogy az megolvadjon? Tételezzük fel, hogy a rugalmatlan ütközés során felszabaduló hő fele a falat, fele pedig az ólomgolyót melegíti.

(4 pont)

megoldás, statisztika

P-jelű feladatok A beküldési határidő 2024. február 15-én LEJÁRT.

---

P. 5535. Árnyékoló napvitorla $\displaystyle 2~\text{m}^2$ felülete közel vízszintes. Hirtelen egyenletesen elkezd esni az eső. A vitorla közepén van egy kicsi lyuk, amelyen az esővíz lefolyik. A vízsugár alá teszünk egy henger alakú edényt, amelynek az alján van egy $\displaystyle 5~\text{mm}^2$ keresztmetszetű lyuk. Az edényben a vízszint emelkedése megáll $\displaystyle 20~\text{cm}$-nél. Határozzuk meg, hogy a 10 percig tartó eső során hány mm csapadék esett!

Közli: Simon Péter, Pécs

(4 pont)

megoldás, statisztika

---

P. 5536. Egy focimeccsen a kaputól valamekkora $\displaystyle d$ távolságban lévő $\displaystyle P$ pontból szabadrúgást végeznek el. A $\displaystyle P$ pont a gólvonal felezőmerőlegesén helyezkedik el.

A játékos a labdát valamekkora $\displaystyle \alpha$ szögben éppen a felső kapufa közepe felé rúgja el, de az $\displaystyle t_1$ idejű mozgás után a gólvonal közepénél esik a földre. A rúgást valamilyen ok miatt meg kell ismételni. Másodszor a játékos erősebben, $\displaystyle 2\alpha$ szögben rúgja el a labdát, ami $\displaystyle t_2$ idő múlva eltalálja a felső kapufa közepét. (A kapu mérete kicsit eltér a szabványostól.)

$\displaystyle a)$ Mekkora volt az $\displaystyle \alpha$ szög?

$\displaystyle b)$ Mekkora a $\displaystyle d$ távolság?

$\displaystyle c)$ Mekkora volt a labda kezdősebessége az első, illetve a második szabad­rúgásnál?

(A labdát tekintsük tömegpontnak, és a közegellenállást ne vegyük figyelembe.)

Adatok: $\displaystyle t_1=1{,}90~\text{s}$, $\displaystyle t_2=1{,}93~\text{s}$, $\displaystyle g=9{,}81~\text{m}/\text{s}^2$.

Nagy Béla (1881–1954) feladata nyomán

(5 pont)

megoldás, statisztika

---

P. 5537. Egy kalandparkban az erre vállalkozók egy $\displaystyle R\!=\!20~\text{m}$ magas, $\displaystyle {\alpha\!=\!30^{\circ}}$-os hajlásszögű lejtő tetejéről ($\displaystyle A$), kezdősebesség nélkül, szabadon (fékezésmentesen) gurulhatnak lefelé egy kicsiny kocsiban. A lejtő törésmentesen csatlakozik egy $\displaystyle R$ sugarú, körív alakú pályaszakaszhoz ($\displaystyle B$), majd a pálya a legmélyebb pontjától ($\displaystyle C$) vízszintesen folytatódik tovább. A vízszintes szakaszon a megfelelő módon fékezett kocsi időben egyenletesen lassul, és $\displaystyle \ell=2R$ út megtétele után a $\displaystyle D$ pontnál megáll.

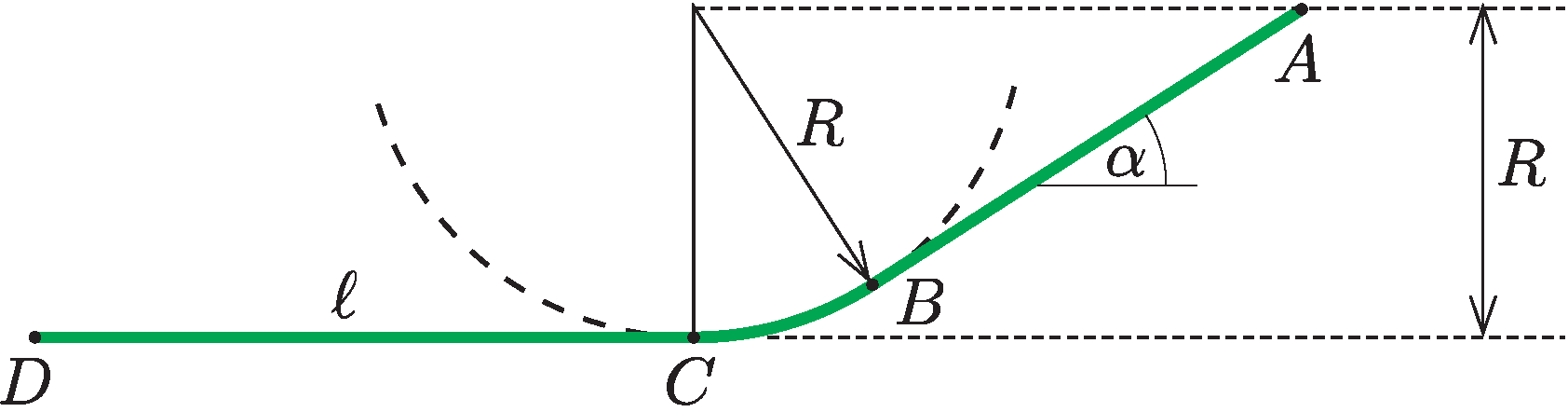
Számítsuk ki, hogy az utasok a szokásos súlyuknak hányszorosát érzik a mozgásuk során! Ábrázoljuk ezt az arányt a megtett út függvényében!

Holics László feladata nyomán

(5 pont)

megoldás, statisztika

---

P. 5538. Sok játszótéren találunk az ábrához hasonló, forgatható mászókát. Egy ilyen mászókán egy hangya mászik fel, miközben az egyenletesen forog. A felfelé kapaszkodó hangya folyamatosan azt érzi, hogy ,,függőlegesen fölfelé'' mászik.

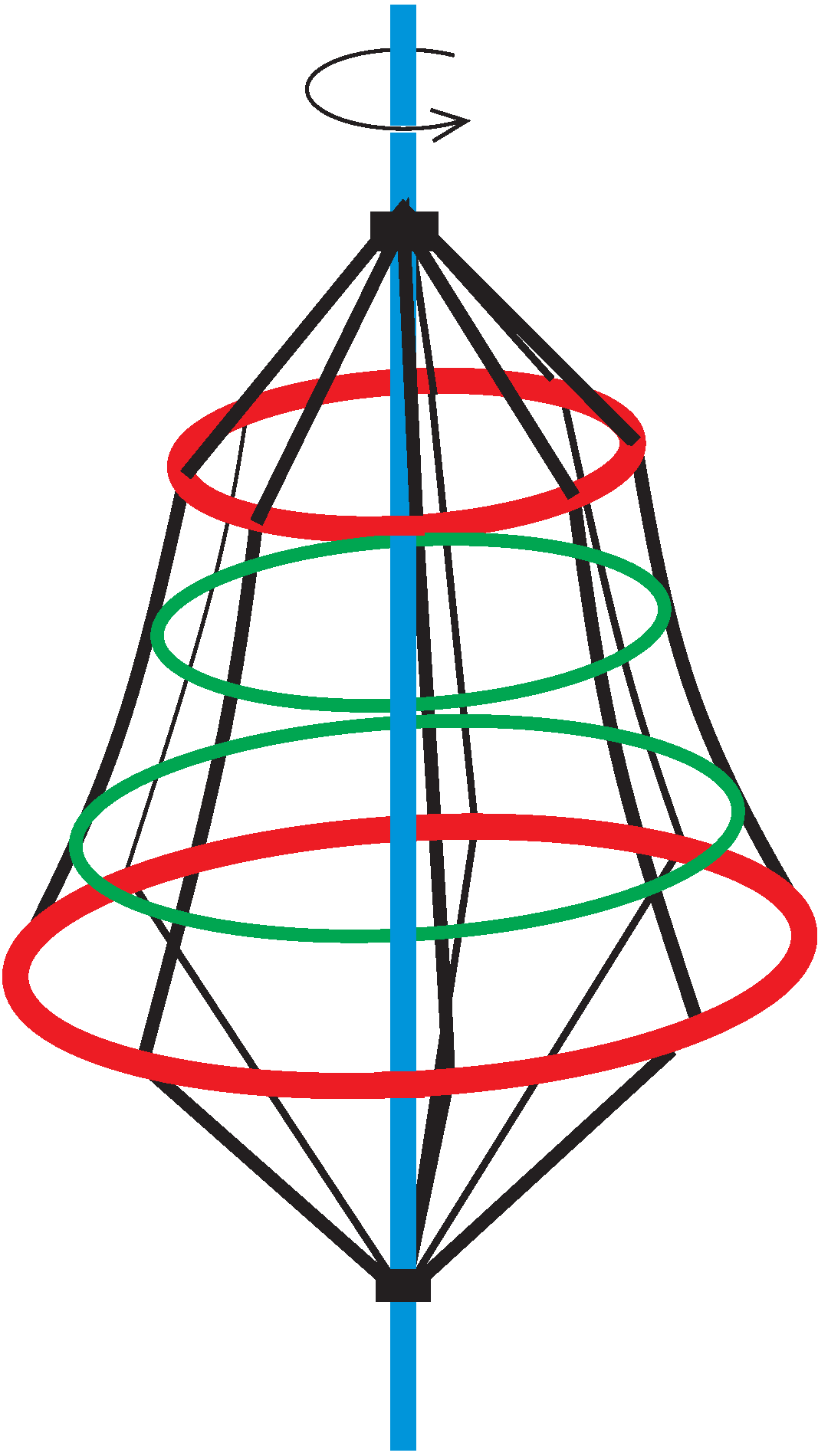
A mászóka köteleit tartó, piros körgyűrűk közül az alsó sugara $\displaystyle 2~\text{m}$, a felsőé $\displaystyle 1~\text{m}$, és a gyűrűk távolsága $\displaystyle 3~\text{m}$. Mekkora fordulatszámmal forog a mászóka?

Közli: Rakovszky Andorás, Budapest

(5 pont)

megoldás, statisztika

---

P. 5539. Egy hosszú, merev, elhanyagolható tömegű palló $\displaystyle n$ egymástól egyenlő távolságra elhelyezett, azonos direkciós erejű és azonos nyújtatlan hosszal rendelkező rugóra van felfüggesztve. Az első rugó legfeljebb $\displaystyle K$ erőt tud kifejteni, a második $\displaystyle 2K$-t, $\displaystyle \ldots$, az $\displaystyle n$-edik $\displaystyle n\cdot K$-t anélkül, hogy elszakadna. Legfeljebb mekkora tömegű testet helyezhetünk el a pallón? Hova kell helyeznünk? (Tételezzük fel, hogy a rugók alig nyúlnak meg.)

Közli: Szentivánszki Soma, Budapest

(5 pont)

megoldás, statisztika

---

P. 5540. Két azonos méretű poharat szobahőmérsékletű teával töltünk meg, majd az egyiket a hűtőbe, a másikat pedig a jóval hidegebb mélyhűtőbe helyezzük. Egy perc elteltével a poharakat kicseréljük, majd egy további percig új helyükön hagyjuk, végül mindkettőt kivesszük. Melyik pohár tartalma hűl le jobban a kísérlet során? A releváns hőátadási folyamatokra alkalmazható a Newton-féle lehűlési törvény, továbbá a hőátadási tényező a hűtő, illetve a mélyhűtő esetén azonosnak tekinthető.

Dürer Verseny feladata nyomán

(5 pont)

megoldás, statisztika

---

P. 5541. A $\displaystyle ^{222}\text{Rn}$ az urán-rádium bomlási sor tagja: $\displaystyle 3{,}8\,$napos felezési idővel alfa-bomló izotóp.

$\displaystyle a)$ Ha az épp átalakuló radonmagot nyugvónak tekintjük, mekkora sebességre tesz szert a leányterméke?

$\displaystyle b)$ Hány MeV az energiája a bomlás során keletkező alfa-részecskének?

Útmutatás: Az izotóptömegek táblázata megtalálható a következő oldalon: https://www.komal.hu/cikkek/atomtomegek.pdf

Közli: Kis Tamás, Heves

(4 pont)

megoldás, statisztika

---

P. 5542. Egy $\displaystyle R$ ellenállásból, egy $\displaystyle L$ induktivitású tekercsből, egy $\displaystyle C$ kapacitású kondenzátorból és egy $\displaystyle U(t)=U_0\sin(\omega t)$ feszültségű generátorból az ábrán látható egyszerű áramkört hozzuk létre.

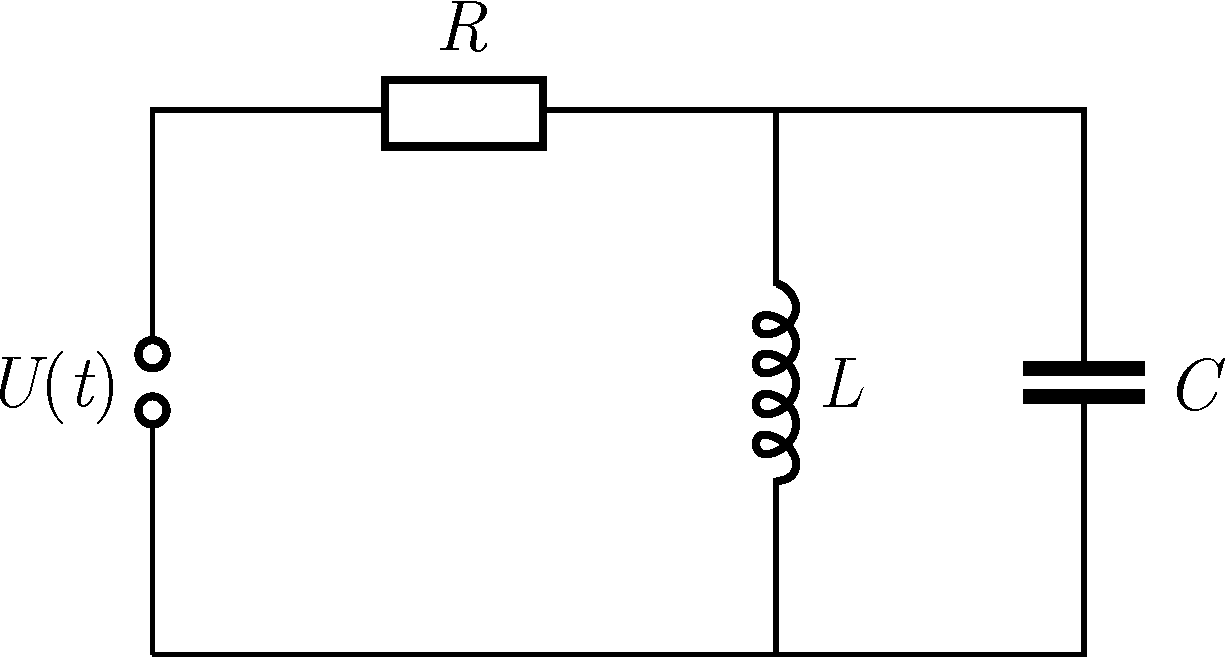
$\displaystyle a)$ Mekkora az ellenálláson átfolyó áram amplitúdója?

$\displaystyle b)$ Hogyan válasszuk meg az $\displaystyle \omega$ körfrekvenciát ahhoz, hogy az ellenálláson ne folyjon áram?

Közli: Németh Róbert, Budapest

(5 pont)

megoldás, statisztika

---

P. 5543. Borús időben egy, az égbolt felé fordított fénymérővel méréseket végzünk. Azt tapasztaljuk, hogy a felhőtakaró fényszórása miatt az egységnyi felületre beeső teljesítmény jó közelítéssel $\displaystyle I_0$ értékű, függetlenül a fénymérő irányítottságától. Egy átlátszatlan, belül kormozott, $\displaystyle R$ sugarú, vékony falú gömbhéj tetején egy kicsiny $\displaystyle r$ sugarú lyuk van (melynek mérete sokkal nagyobb a látható fény hullámhosszánál). Adjuk meg a szabadba helyezett gömbhéj belső felületén a megvilágítás intenzitását!

Közli: Vigh Máté, Biatorbágy

(6 pont)

megoldás, statisztika