A KöMaL 2024. februári fizika feladatai

M-jelű feladatok A beküldési határidő 2024. március 18-án LEJÁRT.

---

M. 429. Egy másfél literes, hengeres üvegpalack kupakját lyukasszuk ki. Töltsük meg a palackot kb. félig vízzel, majd csavarjuk vissza rá a kupakot. Fordítsuk a nyakával lefelé, és mérjük meg, hogy mennyi víz folyik ki belőle. Mérjük meg azt is, hogy a kicsurgás leállásakor mekkora a víz magassága a palackban. A mérési eredmények felhasználásával határozzuk meg, hogy mekkora volt a légnyomás a mérés elvégzésekor.

Közli: Simon Péter, Pécs

(6 pont)

statisztika

G-jelű feladatok A beküldési határidő 2024. március 18-án LEJÁRT.

---

G. 841. Ha $\displaystyle 20$-$\displaystyle 30$ hurkapálcát összegumizunk szorosan, akkor miért vesz föl a köteg közel henger alakot?

Közli: Gelencsér Jenő, Kaposvár

(3 pont)

megoldás, statisztika

---

G. 842. Űrkutatók reményei szerint hamarosan ember által lakott űrbázis épül a Holdon. Képzeljük el, hogy az űrbázis létrehozásának egy éves évfordulóját speciális tűzijátékkal ünneplik meg az űrhajósok. A lövedéket $\displaystyle 45^\circ$-os szögben lövik ki, ami 100 m magasan, a pálya tetőpontján robban szét apró részekre, melyek a lövedék tömegközéppontjához képest $\displaystyle 10~\text{m}/\text{s}$ sebességgel, hosszasan, fényesen világítva repülnek szét. A kilövés helyéhez és idejéhez viszonyítva mikor és hol ér talajt legelőször és legutoljára fényesen világító darabka?

(4 pont)

megoldás, statisztika

---

G. 843. Egy $\displaystyle 45^\circ$-os szögben ferdén elhelyezett síktükör fölött $\displaystyle 12~\text{cm}$ magasan egy $\displaystyle 3~\text{cm}$ hosszú, vízszintes helyzetű világító nyilat helyezünk el. Adjuk meg, hogy mekkora és milyen helyzetű képet hoz létre a tükörtől $\displaystyle 18~\text{cm}$-re lévő, $\displaystyle 20~\text{cm}$ fókusztávolságú gyűjtőlencse!

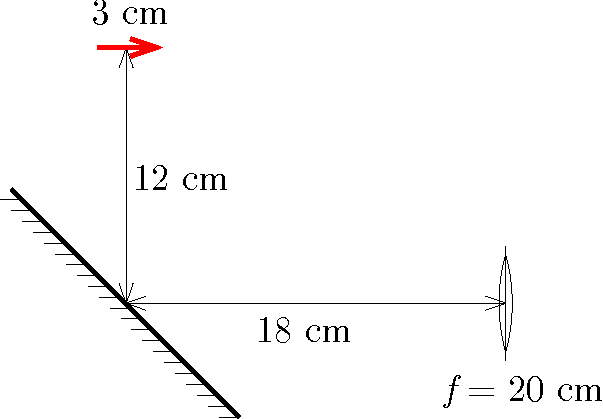
(4 pont)

megoldás, statisztika

---

G. 844. Egy gőzfürdőben lényegében $\displaystyle 42~{}^{\circ}\text{C}$-os felhőben üldögélnek az emberek. Ezzel szemben egy $\displaystyle 95~{}^{\circ}\text{C}$-os finn szaunában a levegő relatív páratartalma mindössze $\displaystyle 12\%$. Hol magasabb a levegő abszolút páratartalma?

(4 pont)

megoldás, statisztika

P-jelű feladatok A beküldési határidő 2024. március 18-án LEJÁRT.

---

P. 5544. Egy különleges krumpliágyú esetében a vízszinteshez képest $\displaystyle \alpha$ szögben kilőtt krumpli kezdősebessége $\displaystyle v_0=(20~\text{m}/\text{s})\cdot \cos\alpha$. A lövedékre ható közegellenállási erőt hanyagoljuk el! Milyen messzire lehet lőni ezzel a krumpliágyúval vízszintes talajon?

Közli: Széchenyi Gábor, Budapest

(4 pont)

megoldás, statisztika

---

P. 5545. Könnyen mozgó dugattyúval elzárt hengerben $\displaystyle 180~\text{g}$ tömegű, héliumból és hidrogénből álló gázkeverékkel állandó nyomáson $\displaystyle 156~\text{kJ}$ hőt közlünk. Ennek hatására a gázkeverék $\displaystyle 56~\text{kJ}$ munkát végzett. Hány g hidrogén volt a hengerben? Mekkora a gázkeverék hőmérséklet-változása?

Közli: Holics László, Budapest

(4 pont)

megoldás, statisztika

---

P. 5546. Az Eszkimók Csodák Palotájában található egy függőleges tengely körül $\displaystyle \omega=\pi/6~\text{s}^{-1}$ szögsebességgel forgó, $\displaystyle R=3~\text{m}$ sugarú, kör alakú jégpályára épített iglu. A forgó igluban két gyerek ül az ábrán látható helyzetben, egymáshoz képest $\displaystyle \varphi=120^\circ$-os szögben. Az $\displaystyle A$ pontban ülőnek sikerül úgy elindítania egy kis méretű korongot, hogy az pont a $\displaystyle B$ helyen ülő társa kezébe érkezzen az indítást követően $\displaystyle t=2~\text{s}$ múlva.

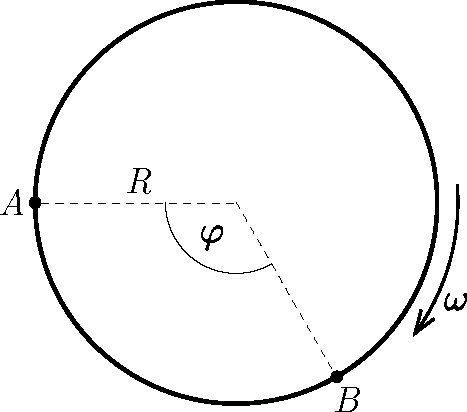
$\displaystyle a)$ Az igluhoz képest mekkora sebességgel és milyen irányba kellett a korongot az $\displaystyle A$ pontban ülő gyermeknek ellöknie?

$\displaystyle b)$ Mekkora távolságra közelíti meg a korong a mozgása során az iglu középpontját?

Közli: Szász Krisztián, Budapest

(5 pont)

megoldás, statisztika

---

P. 5547. Egy kicsi fagolyót $\displaystyle 30~\text{cm}$ hosszú fonálra kötünk, és a fonál szabad végét egy vödör fenekén, a középponttól $\displaystyle 20~\text{cm}$ távolságban rögzítjük. A vödörbe vizet töltünk, és a szimmetriatengelye körül forgatni kezdjük. (A víz mindvégig ellepi a golyót.) Mekkora szögsebességgel kell a vödröt forgatnunk, hogy hosszú idő után a fonál a függőlegessel $\displaystyle 30^\circ$-os szöget zárjon be?

Quantum Magazine nyomán

(5 pont)

megoldás, statisztika

---

P. 5548. Egy kicsiny, lapos hűtőmágnes súlya $\displaystyle G$. A mágnest a hűtőszekrény függőleges oldalára helyezzük, majd a fémlapra merőleges, függőleges síkban valamilyen irányba húzni kezdjük. A legkisebb erő, amivel meg tudjuk mozdítani a mágnest függőlegesen felfelé, $\displaystyle F_1$, lefelé pedig $\displaystyle F_2$.

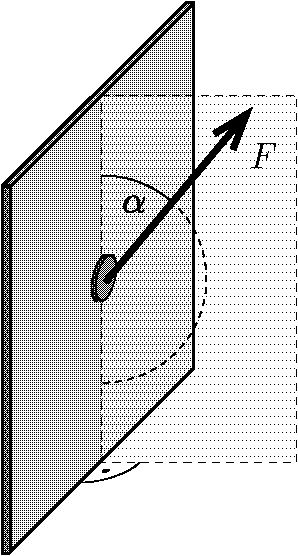
$\displaystyle a)$ Mekkora a mágnes és a hűtőszekrény oldala közötti tapadási súrlódási együttható?

$\displaystyle b)$ Mekkora húzóerővel hat a fémlemez a mágnesre, amikor azt nem húzzuk semerre?

Adatok: $\displaystyle G=0{,}10~\text{N}$, $\displaystyle F_1=0{,}20~\text{N}$ és $\displaystyle F_2=0{,}05~\text{N}$.

(Lásd még a G. 702. számú gyakorlatot a KöMaL 2020. évi 3. számában.)

Közli: Gnädig Péter, Vácduka

(5 pont)

megoldás, statisztika

---

P. 5549. Homogén tömegeloszlású, $\displaystyle M$ tömegű, vékony huzalból zárt síkgörbét hajlítunk. Az így kapott keret tehetetlenségi nyomatéka a tömegközéppontján áthaladó, síkjára merőleges tengelyre vonatkozóan $\displaystyle \Theta_0$. A testtel ezután kísérletet végzünk az ábrán vázolt módon: különböző pontjai mentén felfüggesztjük, majd mérjük a kis amplitúdójú, saját síkjába eső lengéseinek periódusidejét. Mekkora a lehetséges legkisebb lengésidő?

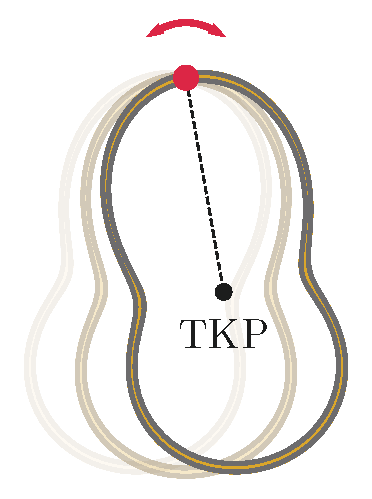
Dürer Verseny feladata nyomán

(5 pont)

megoldás, statisztika

---

P. 5550. Lézerfénnyel megvilágítjuk az $\displaystyle R$ sugarú, $\displaystyle n$ törésmutatójú gömblencsét. Merre kell irányítani az optikai tengelyen a lencse középpontjától $\displaystyle d$ távolságra lévő pontból kiinduló fénysugarat, hogy az a lencsén megtörve a lencse másik oldalán a középponttól ugyancsak $\displaystyle d$ távolságra metssze az optikai tengelyt? Adott törésmutató mellett milyen $\displaystyle d$ estén lehetséges ez a fénysugármenet? Számoljuk ki a kérdéses irány szögét a $\displaystyle {d=2R}$, $\displaystyle {n=3/2}$ adatokkal!

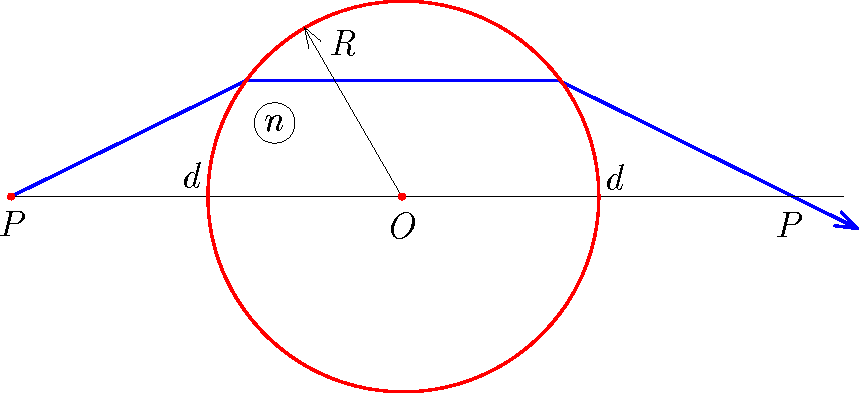
Közli: Cserti József, Budapest

(4 pont)

megoldás, statisztika

---

P. 5551. Egy nagy rendszámú atommag mellett elhaladó, $\displaystyle 2~\text{MeV}$ energiájú fotonból elektron-pozitron pár keletkezik. (A nehéz atommag csak impulzust vesz fel, energiát szinte semmit.) A mágneses térben elhelyezett Wilson-kamrában mindkét részecske ugyanabban a síkban, $\displaystyle 5~\text{cm}$ sugarú köríven mozog. Mekkora a mágneses indukcióvektor nagysága?

Példatári feladat nyomán

(5 pont)

megoldás, statisztika

---

P. 5552. Képzeljük el, hogy az ábrán látható koaxiális kábelen $\displaystyle P$ teljesítményt szállítunk $\displaystyle \ell$ távolságra. A kábel elhanyagolható ellenállású belső vezetékének sugara $\displaystyle a$, a vékony falú, hasonlóan ellenállásmentesnek tekinthető külső cső sugara pedig $\displaystyle b$. Mind a kábelen kívül, mind a belső vezeték és a külső cső között vákuum van, a kábelen egyenáram folyik.

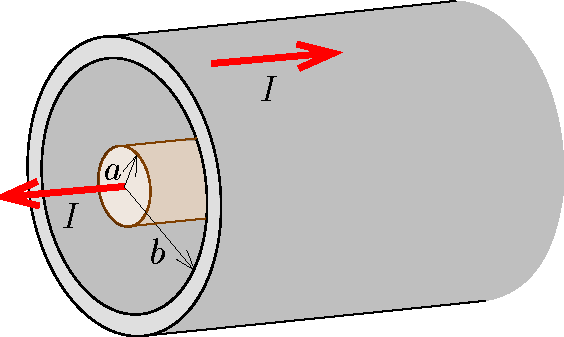
$\displaystyle a)$ Mekkora a távvezeték árama, ha a külső cső falát sem befelé, sem kifelé nem feszíti erő?

$\displaystyle b)$ A koaxiális kábel melyik végén – jobbra vagy balra – van a generátor (tápegység), illetve a fogyasztó (terhelés)?

Közli: Honyek Gyula, Veresegyház

(6 pont)

megoldás, statisztika