A KöMaL 2024. februári informatika feladatai

I-jelű feladatok A beküldési határidő 2024. március 18-án LEJÁRT.

---

I. 615. Adott a koordináta-rendszerben néhány pont, amelyek mindkét koordinátája egész szám. A pontok nem mind esnek egy egyenesre. Körbevesszük ezeket a pontokat egy olyan konvex sokszöggel, amelyet a csúcsok egy része határoz meg és minden pont e sokszög határán vagy belsejében van (a keletkező alakzatot konvex buroknak hívjuk). Adjuk meg a sokszög csúcsainak számát!

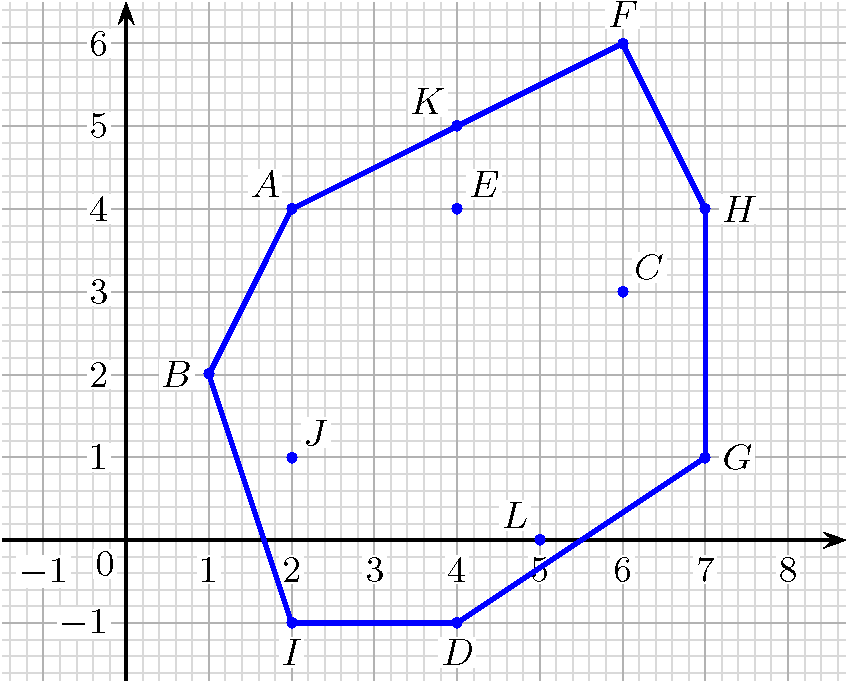
A standard bemenet első sorában a pontok \(\displaystyle N\) száma található (\(\displaystyle 5\leq N\leq 100\)), a következő sorok mindegyikében egy-egy csúcs két egész koordinátája szerepel szóközzel elválasztva.

A program a standard kimenet egyetlen sorába írja ki a körbevételhez szükséges sokszög csúcsainak számát.

Példa:

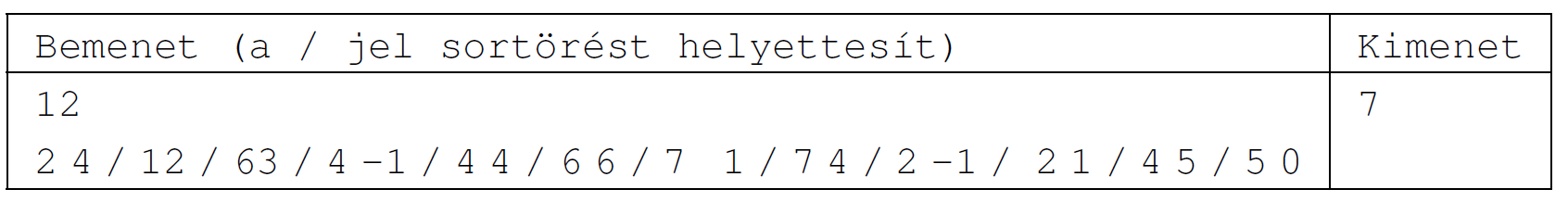
Beküldendő egy tömörített i615.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika

---

I. 616. Egy gyöngysorba különböző színű gyöngyöket fűztek fel a gyerekek. A gyöngyök színét az angol ábécé nagybetűivel adjuk meg.

Készítsünk programot i616 néven, amely a megadja a gyöngysor olyan \(\displaystyle K\) hosszú szakaszát, amelyben a legkevesebb a gyöngyök színének száma.

A program standard bemenetének első sorában a gyöngysor elemszáma \(\displaystyle N\) (\(\displaystyle 1\leq N\leq 10\,000\)) és a gyöngysorszakasz hossza (\(\displaystyle 1<K<N\)) van. Az ezt követő sorban a gyöngyök színeit jelölő nagybetűk vannak szóközzel elválasztva.

A program a standard kimenetre írja ki annak a \(\displaystyle K\) hosszú gyöngysorrészletnek a kezdő sorszámát, amelyen belül a legkevesebb szín van. Több megoldás esetén a kisebb kezdősorszámút írjuk ki.

Beküldendő egy tömörített i616.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben futtatható.

(10 pont)

megoldás, statisztika

---

I. 617. A születéskor várható élettartam változását vesszük górcső alá a 2000-től 2021-ig születettek között a Föld néhány országában.

1. Nyissunk egy üres táblázatkezelő munkafüzetet.
2. Töltsük be egy üres munkalapra az A1-es cellától kezdve az UTF-8 kódolású, tabulátorokkal tagolt adatok.txt fájl tartalmát. Munkánkat mentsük elettartam néven a táblázatkezelő alapértelmezett formátumában.
3. Az A57-es cellába kerüljön válasz az A56-os cellában olvasható kérdésre.
4. Az X3:X46 tartomány celláiban jelenítsük meg, hogy az egyes országokban hány százaléka a 2019-es adat a 2000-es évinek. Az eredmények százalék formátumúak legyenek két tizedesjegy pontossággal.
5. Számítsuk ki a B47:W47 tartomány celláiban, hogy mennyi az európai országok (3–33. sor) éves átlaga.
6. A B48:W48 tartomány celláiba kerüljön a „Jó'' felirat, ha az adott évben az európai átlag elérte vagy meghaladta az Egyesült Államok adatát; különben a cella maradjon üres.
7. Az A50-es cellába kerüljön válasz az A49-es cellában olvasható kérdésre.
8. Az A51-es cella kérdésére válaszként az országok neve a B53-es, a B54-es és a B55-ös cellákba kerüljön, az életkor pedig az E53-as, az E54-es és az E55-ös cellákba.
9. Az Y3:Y46 tartomány celláiba kerüljön a „\(\displaystyle +\)'' jel, ha az adott országban 2019-től 2021-ig folyamatosan nőtt a várható életkor, „\(\displaystyle -\)'' jel, ha folyamatosan csökkent, egyéb esetekben a cella maradjon üres.
10. Készítsük el a minta szerinti grafikont Ausztria, Csehország, Magyarország, Románia és Szlovákia adatairól. A diagramot helyezük új, diagram típusú munkalapra.

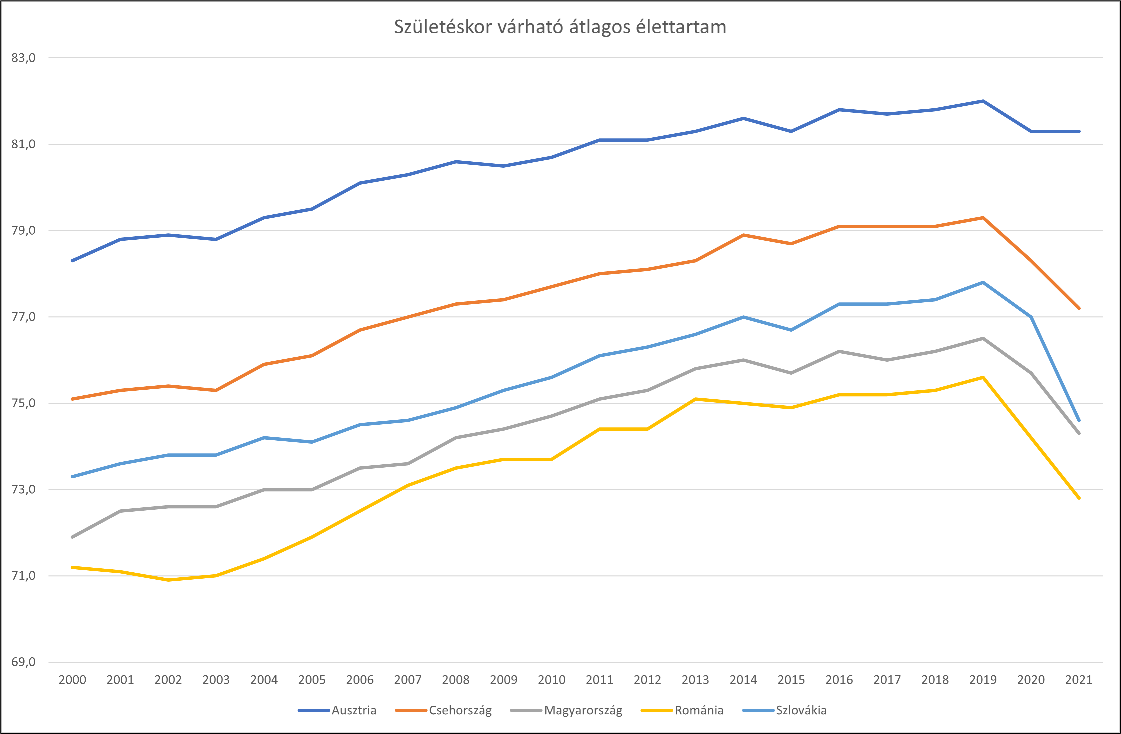
Segédszámításokat az AA oszloptól, illetve a 60. sortól kezdve végezhetünk. A megoldásban saját függvény vagy makró nem használható.

Forrás: https://www.ksh.hu/stadat_files/nep/hu/nep0060.html

Beküldendő egy tömörített i617.zip állományban a táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.

A megoldáshoz szükséges letölthető állomány: adatok.txt

(10 pont)

megoldás, statisztika

---

I. 618. Középosztósnak nevezik azokat a legalább háromjegyű számokat, ahol a szám első és utolsó jegyét elhagyva a kapott szám osztható az első és utolsó jegy összegével. Duplaközéposztósnak nevezik azokat a legalább ötjegyű középosztós számokat, ahol a szám első és utolsó jegyét elhagyva a kapott szám szintén középosztós.

Például \(\displaystyle 2124\) középosztós, mert a közepén lévő szám, ami \(\displaystyle 12\), osztható \(\displaystyle {(2+4=)6}\)-tal. A \(\displaystyle 321243\) dupla középosztós, mert \(\displaystyle 2124\) középosztós, és osztható \(\displaystyle {(3+3=)6}\)-tal. A leírásból következik, hogy a duplaközéposztós számok legalább ötjegyűek.

Állítsuk elő táblázatkezelő segítségével az összes legfeljebb hatjegyű duplaközéposztós számot, és válaszoljunk néhány ezekkel kapcsolatos kérdésre!

1. Nyissunk meg egy üres munkafüzetet, generáljuk a kívánt számokat a munkalap A oszlopába. Mentsük el a munkafüzetet gener néven.
2. Nyissuk meg a kozep.xlsx munkafüzetet és másoljuk át a generált számokat ebbe a munkafüzetbe függőlegesen az A3-as cellától kezdve. Az első szám az A3-as cellában legyen, a számok között ne legyen üres cella.
3. Válaszoljunk az I3:I9 tartomány celláiban függvény segítségével a tőlük balra feltett kérdésekre.

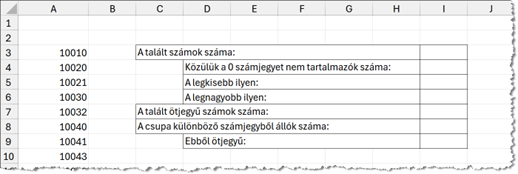
Magyarázatként nézzük a \(\displaystyle 10\,032\) számot: a szélei \(\displaystyle 1\) és \(\displaystyle 2\), ezek összege \(\displaystyle 3\). A szám közepe \(\displaystyle 003\), ami valójában \(\displaystyle 3\); \(\displaystyle 3\) osztható \(\displaystyle 3\)-mal. A középső \(\displaystyle 003\) szélei \(\displaystyle 0\) és \(\displaystyle 3\), összegük \(\displaystyle 3\). A szám közepe \(\displaystyle 0\), és \(\displaystyle 0\) is osztható \(\displaystyle 3\)-mal. Vagy például a \(\displaystyle 797\,562\) szám szélső jegyei \(\displaystyle 7\) és \(\displaystyle 2\), összegük \(\displaystyle 9\), és a közepe, \(\displaystyle 9756\) osztható \(\displaystyle 9\)-cel, a \(\displaystyle 9756\) szélei \(\displaystyle 9\) és \(\displaystyle 6\), összegük \(\displaystyle 15\), és a közepe \(\displaystyle 75\) osztható \(\displaystyle 15\)-tel.

Segédszámításokat a gener munkafüzetben a B oszloptól jobbra, a kozep munkafüzetben a J oszloptól jobbra végezhetünk. A megoldásban saját függvény vagy makró nem használható.

Beküldendő egy tömörített i618.zip állományban a gener és a kozep táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben szerepel a generáláskor alkalmazott módszer, a táblázatkezelő neve, verziószáma.

Letölthető fájl: kozep.xlsx.

(10 pont)

megoldás, statisztika