A KöMaL 2024. márciusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2024. április 15-én LEJÁRT. |
M. 430. Egy hurkapálca egyik végét fogjuk be vízszintesen, a másik végét pedig kezdjük el terhelni. Végezzük el a mérést különböző hosszúságú pálcákkal. Hogyan függ a pálca végének lehajlása a terhelés tömegétől és a pálca szabad részének hosszától? Határozzuk meg a hurkapálca anyagának Young-modulusát!
Közli: Széchenyi Gábor, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2024. április 15-én LEJÁRT. |
G. 845. Egy személyautó és egy tehergépkocsi egyszerre indul el egy derékszögű útkereszteződésből. A személyautó \(\displaystyle 20~\text{m}/\text{s}\), a teherautó \(\displaystyle 15~\text{m}/\text{s}\) nagyságú sebességgel egyenletesen halad. A teherautó 10 perc múlva egy bekötőúthoz érve irányt változtat 90 fokkal, majd ott halad tovább korábbi sebességével. Mekkora távolságra lehet egymástól az autó és a tehergépkocsi a kiindulástól számított 20 perc múlva?
Tarján Imre Országos Emlékverseny, Szolnok
(3 pont)
G. 846. Ha ismerjük a földfelszín méretét, a nehézségi gyorsulást, valamint a légnyomást, akkor ezek segítségével, jó közelítéssel meghatározhatjuk a Föld légkörének teljes tömegét. Végezzük el a számítást! Hogyan lehetséges, hogy a légnyomás időnként számottevően megváltozik, miközben a légkör tömege változatlan?
(3 pont)
G. 847. Egy \(\displaystyle R_1=1~\text{M}\Omega\) ellenállással párhuzamosan kapcsolunk egy \(\displaystyle R_2\) ellenállást, majd fokozatosan további \(\displaystyle R_3,R_4,~\ldots,R_n\) ellenállásokat kapcsolunk párhuzamosan hozzá. Az egyes lépésekben az eredő ellenállás rendre
\(\displaystyle a)\) \(\displaystyle \frac{1}{2}~\text{M}\Omega\), \(\displaystyle \frac{1}{3}~\text{M}\Omega\), \(\displaystyle \frac{1}{4}~\text{M}\Omega\), \(\displaystyle \ldots\), \(\displaystyle \frac{R_1}{n}\);
\(\displaystyle b)\) \(\displaystyle \frac{1}{2}~\text{M}\Omega\), \(\displaystyle \frac{1}{4}~\text{M}\Omega\), \(\displaystyle \frac{1}{8}~\text{M}\Omega\), \(\displaystyle \ldots\), \(\displaystyle \frac{R_1}{2^n}\);
\(\displaystyle c)\) \(\displaystyle \frac{1}{1\cdot2}~\text{M}\Omega\), \(\displaystyle \frac{1}{1\cdot2\cdot3}~\text{M}\Omega\), \(\displaystyle \frac{1}{1\cdot2\cdot3\cdot4}~\text{M}\Omega\), \(\displaystyle \ldots\), \(\displaystyle \frac{R_1}{n!}\).
Mekkorák az egyes esetekben az \(\displaystyle R_2\), \(\displaystyle R_3\), \(\displaystyle \ldots\), \(\displaystyle R_n\) ellenállások?
(4 pont)
G. 848. Hosszú, átlátszó anyagból készült, egyenes henger alaplapjának középpontjában vékony fénysugár lép be a hengerbe a környező levegőből. Milyen törésmutató esetében teljesül, hogy a fénysugár nem léphet ki a henger palástján át a levegőbe?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2024. április 15-én LEJÁRT. |
P. 5553. Egy vékony korong az \(\displaystyle O\) középpontján átmenő, rá merőleges tengely körül állandó \(\displaystyle \beta\) szöggyorsulással forog. A korongon a középpontól \(\displaystyle r\) távolságra jelöljünk ki egy \(\displaystyle P\) pontot. Hogyan függ a \(\displaystyle P\) pont gyorsulásának nagysága és a gyorsulásvektorának az \(\displaystyle OP\) egyenessel bezárt szöge az \(\displaystyle r\) távolságtól?
Nagy Béla (1881–1954) feladata nyomán
(3 pont)
P. 5554. Egy \(\displaystyle 20~\text{cm}^2\) alapterületű pohárban \(\displaystyle 120~\text{g}\), \(\displaystyle 25~^\circ\text{C}\)-os víz van. Beleteszünk egy \(\displaystyle 0~^\circ\text{C}\)-os jégkockát. Amikor a jégkocka teljesen elolvad, a víz pontosan \(\displaystyle 0~^\circ\text{C}\)-osra hűl. A pohár vízértéke \(\displaystyle 40~\text{g}\), azaz a pohár hőkapacitása annyi, mint \(\displaystyle 40~\text{g}\) vízé. Egyéb hőveszteségtől és az üveg hőtágulásától tekintsünk el, de a víz sűrűségének hőmérsékletfüggését vegyük figyelembe.
\(\displaystyle a)\) Mennyi a jégkocka tömege?
\(\displaystyle b)\) Mennyit változik a pohárban a vízszint a jégkocka olvadása közben?
Közli: Simon Péter, Pécs
(4 pont)
P. 5555. Vízszintes, nem teljesen sima asztallapon nyugszik egy \(\displaystyle r\) sugarú korong. A síkon egy nagyobb, \(\displaystyle R=2r\) sugarú korong forgásmentesen csúszik úgy, hogy a középpontja a kis korong érintője mentén mozog. Mindkét korong ugyanabból az anyagból készült és a magasságuk is ugyanakkora.
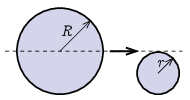
A rugalmasnak tekinthető ütközés után a nagy korong a súrlódás miatt lelassul és \(\displaystyle d=5~\text{cm}\) út megtétele után megáll. Milyen irányban és milyen messzire jut el a kis korong az asztalon? A korongok közötti súrlódás elhanyagolható.
Közli: Holics László, Budapest
(4 pont)
P. 5556. Egy távoli kettőscsillag egyik bolygóján értelmes lények élnek. A csillagászaik megállapították, hogy a két csillag távolsága időben állandó, ezt a távolságot választották ,,csillagászati egységnek'' (CsE). Az űrkutatóik egy érzékeny űrtávcsövet juttattak el a kettős rendszer \(\displaystyle \text{L}_2\) Lagrange-pontjába, amely a kisebb tömegű csillagtól \(\displaystyle \tfrac{1}{2}~\text{CsE}\) távolságra, a másik csillaggal ellentétes oldalon helyezkedik el. Mekkora a két csillag tömegének aránya?
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5557. Egy \(\displaystyle R\) sugarú, vékony falú, rögzített cső belsejében, annak legmélyebb pontjának közelében csúszásmentesen ide-oda gurul egy \(\displaystyle m\) tömegű, \(\displaystyle r\) sugarú, homogén tömegeloszlású henger. Mekkora a mozgás periódusideje?
Közli: Gelencsér Jenő, Kaposvár
(5 pont)
P. 5558. Az ábrán látható háromnegyed kör sugara \(\displaystyle R\), a hiányos négyzet oldalainak hosszúsága \(\displaystyle a\). A zárt vezető körben \(\displaystyle I\) erősségű áram folyik. Határozzuk meg a mágneses indukcióvektor értékét a kör \(\displaystyle O\) középpontjában!
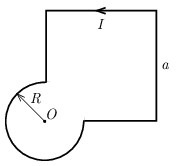
Útmutatás: Egy \(\displaystyle \ell\) oldalhosszúságú, \(\displaystyle I\) árammal átjárt, négyzet alakú vezetőkeret középpontjában a mágneses indukció értéke:
\(\displaystyle B=\frac{2\sqrt{2}\mu_0I}{\pi\ell}. \)
Közli: Kotek László, Pécs
(4 pont)
P. 5559. Kis nyílásszögű, \(\displaystyle R\) sugarú homorú és domború gömbtükröket az ábrán látható módon helyezünk el egymástól \(\displaystyle 1{,}25 R\) távolságra.
A közös optikai tengely mely \(\displaystyle T\) pontjába helyezzünk egy pontszerű fényforrást, hogy a belőle induló fénysugarak a két tükörről való visszaverődés után a \(\displaystyle T\) ponton menjenek át?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5560. Egy ismeretlen bolygón működő \(\displaystyle 500~\text{kHz}\)-es középhullámú rádióállomás \(\displaystyle 314~\text{Hz}\) frekvenciájú búgást sugároz AM modulációval. (Ez a frekvencia nyugtató hatással van a bolygón lakó intelligens életformára.) Érzékeny rádióval egy, a bolygótól a fénysebesség 80%-ával távolodó űrhajóban éppen ezt az adást fogják.
\(\displaystyle a)\) Milyen frekvenciára állítsák a rádió vevőjét?
\(\displaystyle b)\) Milyen frekvenciájúnak hallják a búgást az űrhajósok?
Közli: Rakovszky Andorás, Budapest
(5 pont)
P. 5561. Egy két végén rögzített, hosszegységenként \(\displaystyle \mu\) tömegű, \(\displaystyle 2L\) hosszúságú megfeszített húron a transzverzális hullámok terjedési sebessége \(\displaystyle c\).
\(\displaystyle a)\) Adjuk meg a húr sajátrezgéseinek lehetséges frekvenciáit \(\displaystyle c/L\) egységekben!
\(\displaystyle b)\) A húr közepére egy \(\displaystyle M=2\mu L\) tömegű, pontszerű testet rögzítünk, ahogy az az ábrán látható. Írjunk fel egy egyenletet a húr sajátrezgéseinek lehetséges frekvenciáira, és számítsuk is ki a legalacsonyabb 3 frekvencia számszerű értékét \(\displaystyle c/L\) egységekben! A gravitáció hatása elhanyagolható.
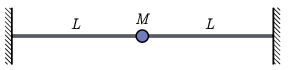
Útmutatás: Belátható, hogy a hullámalakok a középpontra nézve páros vagy páratlan függvényekkel írhatóak le.
Közli: Vigh Máté, Biatorbágy
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)