A KöMaL 2024. márciusi informatika feladatai

I-jelű feladatok A beküldési határidő 2024. április 15-én LEJÁRT.

I. 619. Képezzünk egy pozitív egész számból egy újabb pozitív egész számot úgy, hogy a szám önmagán kívüli legnagyobb osztóját a szám végére írjuk, és a szám elejéről elhagyunk annyi számjegyet, ahányat a végére írtunk. Például $\displaystyle 10$ esetén a kapott szám a $\displaystyle 05$, vagyis az $\displaystyle 5$ lesz, illetve $\displaystyle 125$ esetén az előállított szám az $\displaystyle 525$. Ha a szám $\displaystyle 1$, akkor a képzés nem változtat a számon, marad $\displaystyle 1$.

Készítsünk programot, amely adott lépésszámmal alkalmazza a képzési szabályt a beolvasott számból kiindulva, majd adjuk meg a kimeneten az utoljára előállított számot.

A program a standard bemenet egyetlen sorából olvassa be az első számot ($\displaystyle {1\leq A\leq 1\,000\,000}$), amelyre a képzési szabályt alkalmazzuk, majd az ismétlések ($\displaystyle {1\leq N\leq 100}$) számát. A program a standard kimenet egyetlen sorában az utolsóként képzett számot jelenítse meg.

Példák:

Beküldendő egy tömörített i619.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika

I. 620. Legyen egy helyi értékes számrendszerben az első helyiérték $\displaystyle 1$, a további helyiértékeken pedig a prímszámok növekvő sorozata. Az ebben a számrendszerben felírt $\displaystyle 10101_p$ ötjegyű szám esetén a helyi értékek $\displaystyle 7$, $\displaystyle 5$, $\displaystyle 3$, $\displaystyle 2$, $\displaystyle 1$, azaz a szám értéke $\displaystyle 7\cdot 1+3\cdot 1+1=11$. Tetszőleges nemnegatív egész szám felírható az így megadott számrendszerben, de a felírás nem egyértelmű. Például a $\displaystyle 11$ felírható $\displaystyle 100000_{p}$ alakban is. Tegyük egyértelművé az átváltást úgy, hogy minden esetben azt a felírást választjuk, amelyben csak $\displaystyle 0$-s és $\displaystyle 1$-es számjegy szerepel, és emellett a legkevesebb $\displaystyle 1$-es fordul elő. Így például minden prímszám pontosan egy $\displaystyle 1$-esből és $\displaystyle 0$-kból áll.

Készítsünk programot, amely bekér egy pozitív egész számot, majd megadja a szám felírását a bemutatott számrendszerben. A program a standard bemenet egyetlen sorából olvassa be a számot ($\displaystyle {1\leq a\leq 100\,000}$), majd a standard kimenet egyetlen sorában adja meg a szám felírását a fent leírt módszerrel.

Példák:

A megoldáshoz felhasználható a https://t5k.org/lists/small/10000.txt címen megtalálható szöveges állomány, amely az első 10000 prímszámot tartalmazza. Az állomány letöltés után szerkeszthető, a feldolgozás szempontjából felesleges sorok törölhetők.

Beküldendő egy tömörített i620.zip állományban a program forráskódja és a prímszámokat tartalmazó állomány, valamint egy rövid dokumentáció, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika

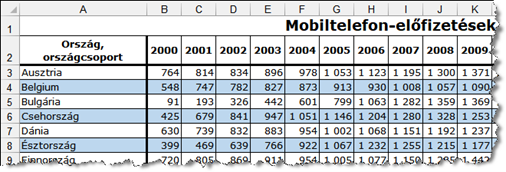
I. 621. Ebben a feladatban a Föld néhány országában az ezer főre vetített mobil-előfizetések számát vizsgáljuk 2000–2022 között.

1. Nyissunk egy üres táblázatkezelő munkafüzetet.
2. Töltsük be egy üres munkalapra az A1 cellától kezdve az UTF-8 kódolású, tabulátorokkal tagolt mobiladat.txt fájl tartalmát. Munkánkat mentsük mobil néven a táblázatkezelő alapértelmezett formátumában.
3. A munkalapon végezzük el az alábbi formázásokat, ügyelve arra, hogy minden oszlop legyen olyan széles, hogy minden adat teljes terjedelmében látható legyen.
1. A munkalap alap betűtípusa Verdana legyen, a betűmérete 10 pontos.
2. Egyesítsük az A1$\displaystyle \,$:$\displaystyle \,$X1 cellákat, a cím legyen félkövér betűstílusú, a betűmérete legyen 14 pontos.
3. Az A2$\displaystyle \,$:$\displaystyle \,$X46 tartomány celláit keret válassza el egymástól, a tartomány első és második sora, illetve első és második oszlopa között a keret legyen vastag vonalú.
4. Az előző pontban említett tartomány első sora legyen dupla magas, a szövegek félkövéren, vízszintesen és függőlegesen középre igazítva jelenjenek meg, esetleg sortöréssel.
5. A berácsozott részre a 4., 6. és minden további páros sorban állítsunk be halványkék háttérszínt.
6. A B3$\displaystyle \,$:$\displaystyle \,$X47 tartomány adatainak megjelenésénél legyen ezres tagolás.



4. Az Y1 cellába gépeljük be a „2010/2000'' szöveget, és számítsuk ki alatta, hogy országonként hányszorosa lett a 2010-es adat a 2000-es évinek. Az adatok százalék formátumban, tizedesjegyek nélkül legyenek láthatók.
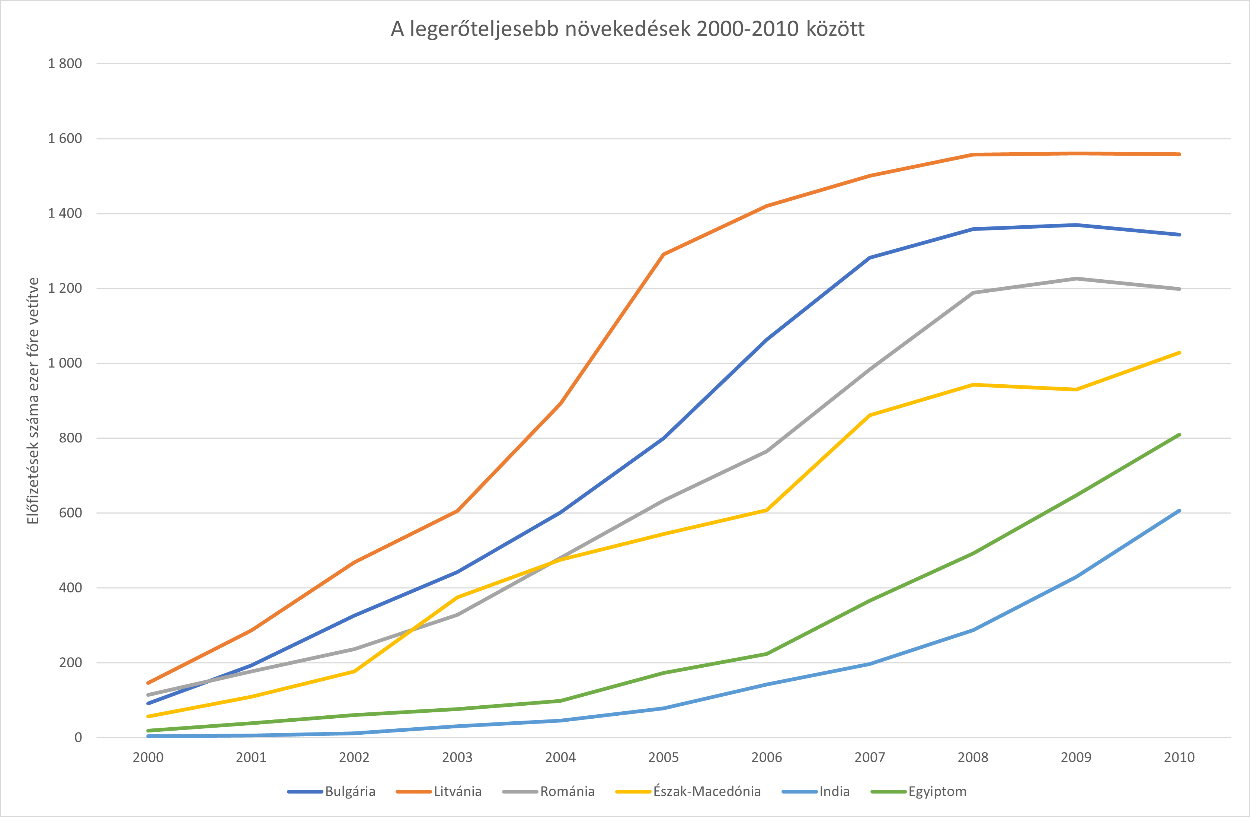
5. Emeljük ki feltételes formázással: sötétzöld háttérszínnel és félkövér betűstílussal és sárga betűszínnel az 1000%-ot meghaladó adatokat.
6. Készítsünk a minta szerinti vonaldiagramot új, diagram típusú munkalapra az előző pontban kiemelt országok 2000–2010 közti adatairól.



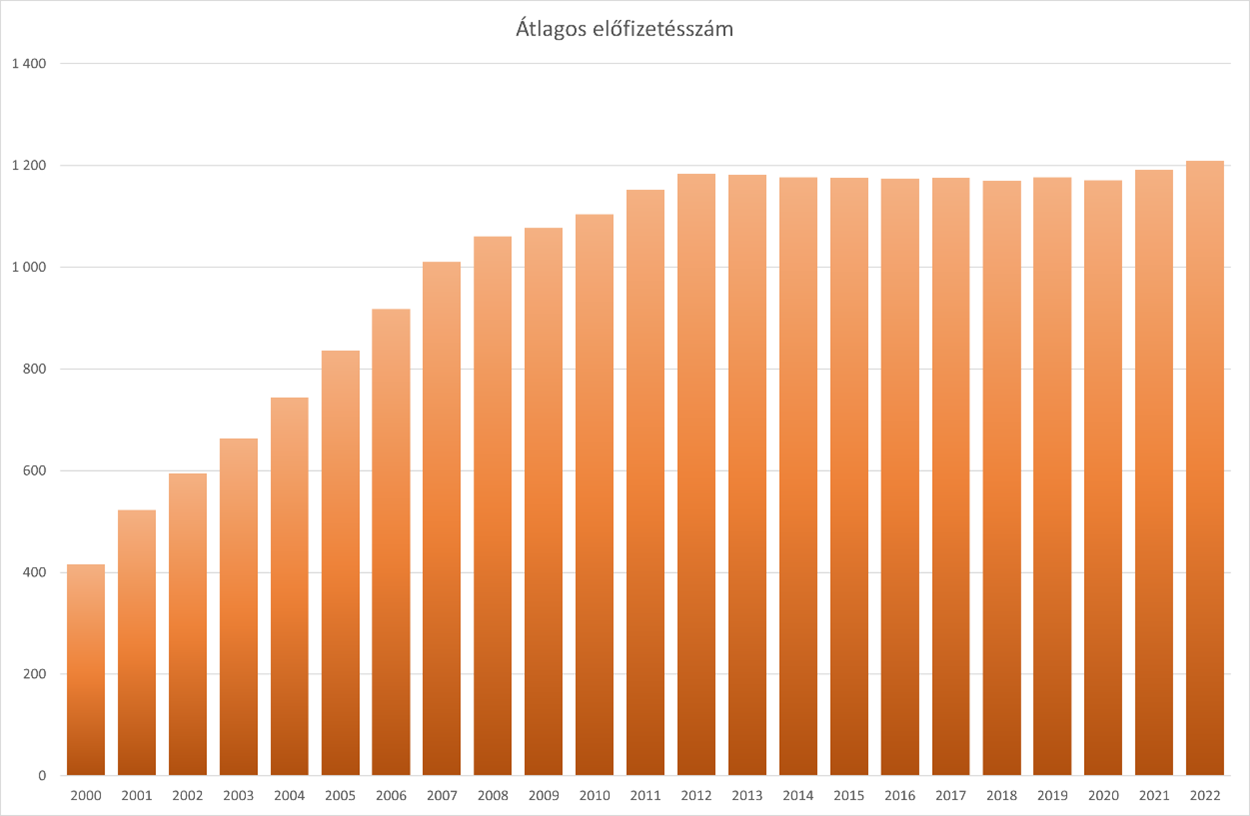
7. A B47$\displaystyle \,$:$\displaystyle \,$X47 tartomány celláiba számítsuk ki az adott év átlagát az adott országok tekintetében, az átlagok egészre kerekítve látszódjanak.
8. Készítsük el az átlagokból a minta szerinti vonaldiagramot, a Z47-es cellába gépeljük be azt az évszámot, amikortól a grafikonról leolvashatóan megkezdődött a stagnálás.



9. A B48$\displaystyle \,$:$\displaystyle \,$X48 tartomány celláiba kerüljön „$\displaystyle +$'' jel, ha az adott év Magyarországi adata meghaladta az EU átlagát, különben a cella maradjon üres.
10. A B49$\displaystyle \,$:$\displaystyle \,$X49 tartomány celláiba kerüljön azon országok száma, amelyekben az adott év előfizetéseinek száma meghaladja a fejenként egy előfizetést.

A megoldásban saját függvény vagy makró nem használható.

Beküldendő egy tömörített i621.zip állományban a táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.

Forrás: https://www.ksh.hu/stadat_files/ikt/hu/ikt0027.html

Letölthető fájl: mobiladat.txt

(10 pont)

megoldás, statisztika

I. 622. Téglalapokból álló és kevés színt tartalmazó ábrákat tömörítve tárolunk. Minden egyes sorról csak azt tartalmazza a tömörített állomány, hogy mi változott az előző sorhoz képest. Ha egy sor megegyezik az előzővel, akkor a tömörített állományban erről nem szerepel bejegyzés.

Készítsünk programot i622 néven, amely előállítja az ábra SVG típusú vektorgrafikus képét.

A program standard bemenetének első sorában a kép sorainak $\displaystyle N$ ($\displaystyle 1\leq N\leq 100$) száma és oszlopainak $\displaystyle M$  ($\displaystyle 1\leq M\leq 100$) száma van. A következő sorok a kódolt képet tartalmazzák soronként és azon belül oszloponként növekvő sorrendben. Minden sorban az első szám a tömörítetlen kép megfelelő sorát jelenti, a második és a harmadik szám a kezdő és végpozíciót, majd a negyedik nagybetű a szín kódja.

A színeket jelölő nagybetűk: F$\displaystyle \,$=$\displaystyle \,$fehér, P$\displaystyle \,$=$\displaystyle \,$piros, K$\displaystyle \,$=$\displaystyle \,$kék, Z$\displaystyle \,$=$\displaystyle \,$zöld, S$\displaystyle \,$=$\displaystyle \,$sárga, N$\displaystyle \,$=$\displaystyle \,$narancs, L$\displaystyle \,$=$\displaystyle \,$lila, B$\displaystyle \,$=$\displaystyle \,$fekete.

A program a standard kimenetre írja ki az ábra SVG kódját.

Az SVG állomány szerkezetéről többek között a http://svg.elte.hu/ címen olvashatunk.

Beküldendő egy tömörített i622.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika