A KöMaL 2024. márciusi matematika feladatai

K-jelű feladatok A beküldési határidő 2024. április 10-én LEJÁRT.

---

K. 804. Egy focimérkőzés végeredménye $\displaystyle 4:3$ lett a hazai csapat javára. Hányféleképpen alakulhatott ki ez a végeredmény, ha volt olyan időszaka a mérkőzésnek, amikor a vendégcsapat vezetett?

(5 pont)

megoldás, statisztika

---

K. 805. Rajzoljunk egy kis szabályos háromszöget, majd a következő ábrán ezt a háromszöget rakjuk körbe ugyanilyen kis háromszögekkel egy rétegben úgy, hogy egy nagyobb szabályos háromszöget kapjunk, majd ezt a második háromszöget is rakjuk körbe kis szabályos háromszögekkel úgy, hogy egy nagyobb szabályos háromszöget kapjunk, és így tovább.

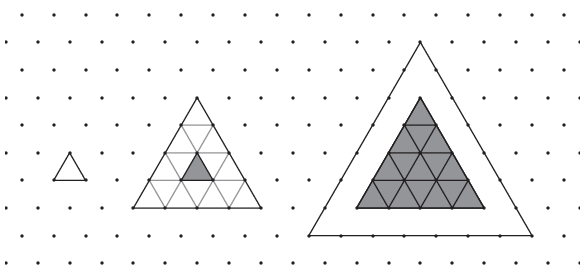
$\displaystyle a)$ Hány kis háromszögből áll a huszadik ilyen háromszög?

$\displaystyle b)$ Hány kis háromszögből áll az $\displaystyle n$-edik ilyen háromszög?

(5 pont)

megoldás, statisztika

---

K. 806. Gizinek a $\displaystyle {\dfrac{4}{x-2}>5}$ egyenlőtlenséget kellett volna megoldania. A megoldás során azonban az 5 helyett egy másik pozitív egész számot írt, így – helyes lépések után – az általa kapott megoldás $\displaystyle 2<x<4$ lett. Milyen pozitív egész számot írt az $\displaystyle 5$ helyett?

(5 pont)

megoldás, statisztika

K/C-jelű feladatok A beküldési határidő 2024. április 10-én LEJÁRT.

---

K/C. 807. Hányféleképpen színezhetünk ki egy $\displaystyle 3\times3$-as rózsaszín táblán három mezőt zöldre, ha azokat a színezéseket nem tekintjük különbözőnek, amelyek tükrözéssel vagy elforgatással egymásba vihetőek?

Javasolta: Fried Katalin (Budapest), Korándi József (Budapest)

(5 pont)

megoldás, statisztika

---

K/C. 808. Egy valós szám és reciproka összegének négyzete $\displaystyle 5$.

$\displaystyle a)$ Határozzuk meg a szám négyzetének és négyzete reciprokának összegét a szám kiszámítása nélkül.

$\displaystyle b)$ Határozzuk meg a szám köbének és köbe reciprokának összegét a szám kiszámítása nélkül.

(5 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2024. április 10-én LEJÁRT.

---

C. 1803. Hány olyan pozitív egész számokból álló számhármas van, amelyben a három szám legnagyobb közös osztója $\displaystyle 4$, legkisebb közös többszöröse pedig $\displaystyle 2024$?

Javasolta: Kozma Katalin Abigél (Győr)

(5 pont)

megoldás, statisztika

---

C. 1804. Az $\displaystyle ABC$ háromszög $\displaystyle BC$, $\displaystyle CA$, $\displaystyle AB$ oldalainak felezőpontja rendre $\displaystyle D$, $\displaystyle E$, $\displaystyle F$. Az $\displaystyle AFE$, $\displaystyle BDF$, $\displaystyle CED$ háromszögek beírt köreinek középpontja rendre $\displaystyle K_a$, $\displaystyle K_b$, $\displaystyle K_c$. Bizonyítsuk be, hogy a $\displaystyle K_aFDE$, $\displaystyle K_bDEF$ és $\displaystyle K_cEFD$ négyszögek területének összege az $\displaystyle ABC$ háromszög területével egyenlő.

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

C. 1805. Oldjuk meg a $\displaystyle \dfrac{6x-3}{3x}-\bigl(3y^2-14xy+8x\bigr)^2=x$ egyenletet, ha $\displaystyle x$, $\displaystyle y$ pozitív valós számok.

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

C. 1806. Egy okostelefon banki applikációja a belépéshez négyjegyű PIN-kódot kér, de biztonsági okokból mindig véletlenszerűen osztja ki a számjegyeket az ábrán látható billentyűhelyekre úgy, hogy minden lehetséges kiosztás valószínűsége azonos. (Egy lehetséges kiosztás szerepel az ábrán.) Ha négy különböző számjegyből áll a PIN-kódunk, akkor mekkora a valószínűsége annak, hogy két belépés során ugyanazokban a pozíciókban hagyunk ujjlenyomatot?

Javasolta: Gáspár Merse Előd (Budapest)

(5 pont)

megoldás, statisztika

---

C. 1807. Legyen $\displaystyle ABC$ egy olyan háromszög, amelyben igaz, hogy $\displaystyle 2\beta=3\gamma$. Legyenek a $\displaystyle D$ és az $\displaystyle E$ az $\displaystyle AC$ oldal pontjai úgy, hogy $\displaystyle BD$ és $\displaystyle BE$ a $\displaystyle \beta$ szöget harmadolják, és a $\displaystyle D$ pont az $\displaystyle A$ és az $\displaystyle E$ közé essen. Továbbá $\displaystyle F$ legyen az $\displaystyle AB$ oldal és a $\displaystyle \gamma$ szögfelezőjének metszéspontja. Igazoljuk, hogy $\displaystyle BE$ és $\displaystyle DF$ párhuzamosak.

Svájci versenyfeladat

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2024. április 10-én LEJÁRT.

---

B. 5374. Az $\displaystyle AB$ szakasz egyik oldalára megrajzoltuk az $\displaystyle ABCD$ négyzetet, a másik oldalára pedig a $\displaystyle BAEF$ rombuszt. A négyzet középpontja legyen $\displaystyle K$, a rombuszé $\displaystyle M$. Bizonyítsuk be, hogy $\displaystyle KM$ felezi az $\displaystyle AMB$ szöget.

Javasolta: Vígh Viktor (Sándorfalva)

(3 pont)

megoldás, statisztika

---

B. 5375. Oldjuk meg a nemnegatív egész számpárok halmazán az $\displaystyle (m-k)^{2}=m+k$ egyenletet.

Javasolta: Németh László (Fonyód)

(4 pont)

megoldás, statisztika

---

B. 5376. Tekintsük a pozitív egész $\displaystyle n$ számot, és osszuk el maradékosan az összes nála kisebb pozitív egésszel. Jelölje $\displaystyle f(n)$ az osztás során fellépő osztási maradékok összegét. (Például $\displaystyle n=5$ esetén a maradékok $\displaystyle 1$-gyel, $\displaystyle 2$-vel, $\displaystyle 3$-mal és $\displaystyle 4$-gyel osztva rendre: $\displaystyle 0$, $\displaystyle 1$, $\displaystyle 2$ és $\displaystyle 1$, azaz $\displaystyle f(5)=4$.)

Oldjuk meg az $\displaystyle f(n)=n$ egyenletet.

Javasolta: Sztranyák Attila (Budapest)

(4 pont)

megoldás, statisztika

---

B. 5377. Határozzuk meg azoknak a $\displaystyle p$ valós számoknak a halmazát, amelyekre

$\displaystyle \sqrt{a^2+b^2-ab}+ \sqrt{b^2+c^2-bc}\geq \sqrt{a^2+c^2-p\cdot ac}$

teljesül minden pozitív valós $\displaystyle a$, $\displaystyle b$, $\displaystyle c$ számhármas esetén, ahol a kifejezések értelmezve vannak.

Javasolta: Nagy Zoltán Lóránt (Budapest)

(4 pont)

megoldás, statisztika

---

B. 5378. Legyenek $\displaystyle n$ és $\displaystyle k$ pozitív egész számok. Bizonyítsuk be, hogy ha $\displaystyle n \leq k^{11}$, akkor $\displaystyle n$ felírható tíz olyan pozitív egész szám szorzataként, melyek közt nincs $\displaystyle k^2$-nél nagyobb összetett szám.

Javasolta: Pach Péter Pál (Budapest)

(5 pont)

megoldás, statisztika

---

B. 5379. Az $\displaystyle ABC$ háromszög $\displaystyle C$ csúcsánál derékszög van. A $\displaystyle C$-ből induló magasságvonal és szögfelező talppontja az $\displaystyle AB$ átfogón $\displaystyle H$, illetve $\displaystyle D$. Az $\displaystyle AHC$ szög felezője az $\displaystyle AC$ oldalt az $\displaystyle E$, a $\displaystyle CHB$ szög szögfelezője pedig a $\displaystyle BC$ oldalt az $\displaystyle F$ pontban metszi. Jelöljük ki a $\displaystyle HE$ szakaszon az $\displaystyle M$, a $\displaystyle HF$ szakaszon pedig az $\displaystyle N$ pontot úgy, hogy $\displaystyle HM: HE= HN : HF$ teljesüljön. Mutassuk meg, hogy a $\displaystyle CD$, $\displaystyle AM$ és $\displaystyle BN$ egyenesek egy ponton mennek át.

Javasolta: Nguyen Duy Khanh (Vietnám)

(5 pont)

megoldás, statisztika

---

B. 5380. Legalább hányadfokú az $\displaystyle f$ egyváltozós polinomfüggvény, ha értékkészlete különbözik $\displaystyle f\circ f$ értékkészletétől, de $\displaystyle f\circ f$ és $\displaystyle f\circ f\circ f$ értékkészlete megegyezik? (A $\displaystyle \circ$ a függvénykompozíció műveletét jelöli.)

Javasolta: Hujter Bálint (Budapest)

(6 pont)

megoldás, statisztika

---

B. 5381. Adott az $\displaystyle \Omega_1$ körbe írt $\displaystyle ABCDEFGH$ nyolcszög, és $\displaystyle \Omega_1$ belsejében az $\displaystyle \Omega_2$ kör. Tegyük fel, hogy az $\displaystyle \omega_1$, $\displaystyle \omega_2$, $\displaystyle \omega_3$, $\displaystyle \omega_4$ körök kívülről érintik $\displaystyle \Omega_2$-t, továbbá $\displaystyle \omega_1$ belülről érinti az $\displaystyle \Omega_1$ kör $\displaystyle AB$ ívét, az $\displaystyle AF$ és a $\displaystyle BE$ szakaszt; $\displaystyle \omega_2$ belülről érinti a $\displaystyle CD$ ívet, a $\displaystyle CH$ és a $\displaystyle DG$ szakaszt; $\displaystyle \omega_3$ belülről érinti az $\displaystyle EF$ ívet, az $\displaystyle AF$ és a $\displaystyle BE$ szakaszt; végül $\displaystyle \omega_4$ belülről érinti a $\displaystyle GH$ ívet, a $\displaystyle CH$ és a $\displaystyle DG$ szakaszt az ábra szerint. Mutassuk meg, hogy az $\displaystyle AF$, $\displaystyle BE$, $\displaystyle CH$ és $\displaystyle DG$ szakaszok által bezárt négyszögbe kört lehet írni.

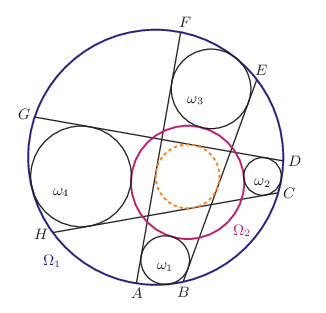
Javasolta: Kós Géza (Budapest)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2024. április 10-én LEJÁRT.

---

A. 875. $\displaystyle a)$ Két játékos egy kooperatív játékot játszik. A játék előtt megbeszélhetnek egy stratégiát, de a kezdés után nem beszélhetnek, és nem tudnak egymásról semmit. A játékvezető minden kör előtt szabadon dönt, hogy abban a körben melyik játékos következzen. Egy körben a soron lévő játékos megtippelheti, hogy hányadik kör van. A játékos tudja, hogy ez hányadik kör, amikor őt választotta a játékvezető, de semmit nem tud arról, hogy a másik játékos hányszor került sorra. Ha helyes a tipp, akkor kapnak egy pontot. A játékosok arról sem kapnak visszajelzést, hogy szereztek-e pontot. A játékosok akkor nyernek, ha összegyűjtöttek 100 pontot. Létezik-e olyan stratégia, amellyel biztosan nyernek véges sok körön belül?

$\displaystyle b)$ Mi a helyzet akkor, ha a többi feltételt nem változtatva a játékosok a körükben kettőt is tippelhetnek, és ha valamelyik tippük helyes, akkor kapnak egy pontot?

Javasolta: Szűcs Gábor, (Budapest)

(7 pont)

megoldás, statisztika

---

A. 876. Keressük meg az összes $\displaystyle a$ és $\displaystyle b$ nemnegatív egész számot, amelyekre $\displaystyle {5^a+6=31^b}$ teljesül.

Javasolta: Füredi Erik (Budapest)

(7 pont)

megoldás, statisztika

---

A. 877. Az $\displaystyle ABCD$ konvex érintőnégyszög beírt köre $\displaystyle \omega$. $\displaystyle \omega$ egyik $\displaystyle AC$-vel párhuzamos érintője a $\displaystyle BD$ átlót a körön kívül lévő $\displaystyle P$ pontban metszi. A $\displaystyle P$ pontból az $\displaystyle \omega$-hoz húzott másik érintő $\displaystyle \omega$-t a $\displaystyle T$ pontban érinti. Bizonyítsuk be, hogy $\displaystyle \omega$ és az $\displaystyle ATC$ háromszög körülírt köre érintik egymást.

Javasolta: Nikolai Beluhov (Bulgária)

(7 pont)

megoldás, statisztika