Síkbeli ponthalmazok erős szimmetriatulajdonságokkal

(megjegyzések egy OKTV-feladathoz)

A 2002-2003-as tanévi Országos Középiskolai Tanulmányi Verseny döntőjének egyik feladata (kissé átfogalmazva) a következő állítást tűzte ki bizonyítandóul:

Ha valamely 2003 elemű síkbeli ponthalmaz bármely háromelemű részhalmaza tengelyesen szimmetrikus, akkor van olyan egyenes, amelyre a ponthalmaz mindegyik eleme illeszkedik.

A feladat nem bizonyult nehéznek, örvendetesen sok helyes megoldás született. Jó néhány versenyző megoldásából kitűnt, hogy az állítás 2003 helyett már sokkal kevesebb pontból álló halmazokra is igaz. Volt, aki megjegyezte, hogy egy szabályos ötszög csúcsaiból és a középpontjából álló ponthalmaz mutatja, hogy hatelemű halmazokra nem igaz az állítás, és azt sejti, hogy hatnál nagyobb elemszámúakra már igaz.

Az alábbiakban a szóba jöhető ponthalmazok számbavételével igazoljuk ezt a sejtést, majd kitérünk egy-két általánosítási lehetőségre.

3-szimmetrikus halmazok

A sík egy részhalmazát 3-szimmetrikusnak nevezzük, ha bármely háromelemű részhalmaza tengelyesen szimmetrikus. Az alábbi tétel ezeket írja le.

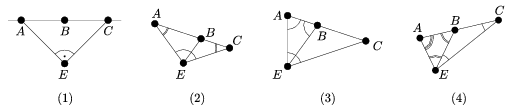
Tétel. A sík egy részhalmaza akkor és csak akkor 3-szimmetrikus, ha része az alábbi 3-szimmetrikus halmazok valamelyikének:

(a) egy egyenes;

(b) egy egyenlő szárú háromszög csúcsai, és a körülírt körének középpontja;

(d) egy négyzet négy csúcsa és a középpontja;

(e) egy szabályos ötszög öt csúcsa és a középpontja;

(f) egy szabályos ötszögnek vesszük négy csúcsát, és a kapott trapézhoz hozzávesszük az átlóinak a metszéspontját;

(g) egy szabályos ötszögnek vesszük négy csúcsát, és a kapott trapézhoz hozzávesszük a szárak meghosszabbításának a metszéspontját;

(h) az alábbi módon származtatott \(\displaystyle {\cal P}\) halmaz. Legyen AECUV egy szabályos ötszög, D a AC és EV átlók metszéspontja, B az AC és EU átlók metszéspontja, és E' az E tükörképe AC-re. Ekkor \(\displaystyle {\cal P}=\{A,B,C,D,E,E'\}\);

Az első ábra a (h) konfigurációt írja le, a második a (k) konfigurációt. Érdemes azonban észrevenni, hogy az első ábrán ABCEU az (f) konfiguráció, ABCE'U és ABCEG pedig a (g) konfiguráció, ahol G az U tükörképe AC-re. Ez utóbbi állítás azért igaz, mert E'BCU és EBCG is egy-egy szabályos ötszög négy csúcsa.

A tételt állítások sorozatával bizonyítjuk. Legyen \(\displaystyle {\cal P}\) egy rögzített 3-szimmetrikus halmaz, amelyről feltesszük, hogy nem kollineáris. Mivel \(\displaystyle {\cal P}\) minden részhalmaza is 3-szimmetrikus, és a fenti tételben (a) kivételével mindegyik konfiguráció legfeljebb hatelemű, feltehető (és fel is tesszük a bizonyítás végéig), hogy \(\displaystyle {\cal P}\) véges.

1. Állítás. Ha \(\displaystyle A,B,C\in{\cal P}\), és a BAC szög legalább derékszög, de nem egyenesszög, akkor AB=AC.

Bizonyítás. Az ABC háromszög tengelyesen szimmetrikus, tehát egyenlő szárú, így a két egyenlő oldallal szemben hegyesszög van. \(\displaystyle \square\)

Először azt az esetet vizsgáljuk, amikor \(\displaystyle {\cal P}\)-ben van három kollineáris pont. E rész bizonyításait is a fenti két ábrán érdemes nyomon követni, igyekeztünk a jelöléseket megtartani.

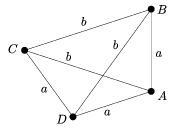
2. Állítás. Tegyük fel, hogy az \(\displaystyle A,B,C\in{\cal P}\) pontok ebben a sorrendben egy e egyenesen helyezkednek el, és \(\displaystyle E\in{\cal P}\) az e egyenesen kívüli pont. Legyen a=AB, c=CB. Ekkor A és C esetleges megcserélése után a következő négy lehetőség egyike áll fenn:

(1) a=c=EB és EA=EC. Ekkor A, E, C egy négyzet három csúcsa, B pedig a középpontja;

(2) EB=c, EA=EC=a. Ekkor az EAC, ECA szögek értéke \(\displaystyle \frac{\pi}{5}\), és az AEC szög értéke \(\displaystyle \frac{3\pi}{5}\);

(3) EA=EB=c és EC=a+c. Ekkor ABE és ACE két hasonló, egyenlő szárú háromszög, melyek szárszöge \(\displaystyle \frac{\pi}{5}\);

(4) EA=a, EB=c és EC=a+c. Ebben az esetben az ACE és BEC szög \(\displaystyle \frac{\pi}{7}\), az ABE és AEB szög \(\displaystyle \frac{2\pi}{7}\), a CAE szög pedig \(\displaystyle \frac{3\pi}{7}\).

A konfiguráció típusát az AEB szög is, az \(\displaystyle \frac{a}{c}\) arány is meghatározza.

Megjegyezzük, hogy a (2) pontban leírt ABCE konfiguráció a (h) ábrán is látható (ugyanazzal a jelöléssel), a (4) pontban leírt ABCE konfiguráció a (k) ábrán található meg, szintén ugyanazzal a jelöléssel, végül a (3) konfiguráció is rajta van a (h) ábrán, mind DBCE, mind ABCG ilyen.

Bizonyítás. Mivel az EBA és EBC szögek összege \(\displaystyle \pi\), az A és C esetleges cseréjével feltehető, hogy az EBC háromszögben B-nél legalább derékszög van. Az 1. Állítás miatt tehát EB=c adódik, és EC>c. Mivel az AEC szög nagyobb, mint a BEC=BCE szög, ezért az AEC háromszögben AC>AE. Ez a háromszög egyenlő szárú és így vagy EA=EC, vagy EC=AC=c+a.

Tegyük fel, hogy EA=EC. Ekkor a CAE, ACE, BEC szögek egyenlők, és az ABE szög ennek kétszerese (a BCE háromszög külső szöge). Ezért az ABE háromszögben az A csúccsal szemközti oldal kisebb, mint a B csúccsal szemközti. Ez a háromszög egyenlő szárú, és így vagy a=AB=BE=BC (ekkor kapjuk az (1) esetet), vagy a=AB=AE (ekkor kapjuk a (2) esetet).

Ha nem EA=EC, hanem EC=AC=a+c teljesül, akkor a CAE és CEA szögek lesznek egyenlők. Ez utóbbi nagyobb, mint a BEA szög, és ezért az ABE háromszögben c=EB>AB=a. Ez is egyenlő szárú háromszög, tehát vagy EA=EB=c (ekkor kapjuk a (3) esetet), vagy EA=AB=a (ekkor pedig a (4) esetet). Mind a négy esetben triviálisan kiszámolhatjuk a felsorolt szögeket. \(\displaystyle \square\)

3. Állítás. Tegyük fel, hogy az \(\displaystyle A,D,B,C\in{\cal P}\) pontok ebben a sorrendben egy e egyenesen vannak, és \(\displaystyle E\in{\cal P}\) az e egyenesen kívüli pont. Ekkor ABCE az előző állítás (2) pontjában leírt alakzat, és D a B pont tükörképe az AC felezőpontjára (lásd a (h) ábrát). Ha \(\displaystyle {\cal P}\) nem kollineáris, akkor egy egyenesen legfeljebb négy pontja lehet.

Bizonyítás. Jelölje F az E merőleges vetületét e-re. Az előző állítás szerint mindkét F kezdőpontú (zárt) félegyenesen legfeljebb két pont lehet \(\displaystyle {\cal P}\)-beli (hiszen F mindegyik előző állításbeli konfigurációban az AC szakasz belső pontja). Tehát F a DB szakasz belső pontja, és mind DBCE, mind BDAE az előző állításban leírt (2), (3), vagy (4) típusú konfiguráció. Az EBD szög meghatározza mindkét konfiguráció típusát, tehát a két típus ugyanaz (és így egyik a másiknak tükörképe az EF egyenesre). Emiatt EB=ED, és akkor mindkét konfiguráció (3) típusú. \(\displaystyle \square\)

4. Következmény. Tegyük fel, hogy \(\displaystyle {\cal P}\) egy 3-szimmetrikus halmaz, melynek van három kollineáris pontja, de nem kollineáris. Ekkor \(\displaystyle {\cal P}\) része a tételben felsorolt alakzatok valamelyikének.

Bizonyítás. Legyenek \(\displaystyle A,B,C\in{\cal P}\) ebben a sorrendben egy e egyenes pontjai. Keressük meg az összes lehetséges \(\displaystyle E\in{\cal P}\) pontot az e egyenesen kívül.

Először azt vizsgáljuk, hogy mikor lehet az ABC pontokhoz az e egyenes ugyanazon oldalán két különböző E pontot illeszteni. A 2. Állításban szereplő négy alakzat hasonlóság erejéig egyértelműen meghatározott. Ezért ha megadjuk az A, B, C pontokat, akkor az E pontot (az e egyenes megadott oldalán) ez egyértelműen meghatározza. Mivel a 2. Állítás megengedi az A és C cseréjét is, így elvileg kétszer négy E pontot illeszthetünk ABC-hez.

Azonban nem minden ABC ponthármashoz lehet E pontot illeszteni, hanem csak azokhoz, ahol az \(\displaystyle \frac{AB}{BC}\) szakaszok aránya megfelelő. Ez az arány a 2. Állításban szereplő négy alakzat esetében más és más. Ha meg a CBA pontokhoz keressük az E pontot, akkor a fenti arány reciprokát kell tekinteni. Az egyetlen lehetséges egybeesés az, amikor az ABC, illetve CBA ponthármasok egyikéhez (2) típusú, a másikhoz (3) típusú alakzatot illesztünk (e ugyanazon oldalára). Így a (h) ábrán is szereplő E, illetve G pontokat kapjuk, ez a (g) konfiguráció, ami tehát az egyetlen, ahol e egyik oldalán legalább két pont szerepel.

Másodszor azt vizsgáljuk, hogy az egyenes két oldalán egyszerre milyen E pontok lehetnek. Az \(\displaystyle \frac{AB}{BC}\) arány meghatározza, hogy milyen típusú alakzatot építhetünk ABC-re, illetve CBA-ra. A típusokat ismét nem lehet keverni, kivéve, hogy a (2)-nek megfelelő alakzathoz hozzátehetjük a (3)-nak megfelelő alakzatot az egyenes túloldalára. Ekkor kapjuk a tételbeli lista (f) elemét (a (h) ábrán ABCEU). A 2. Állításban szereplő (1) és (4) alakzatot, illetve a 3. Állításban szereplő alakzatot is tükrözhetjük e-re, ekkor (d), (k), illetve (h) adódik.

Ahhoz, hogy több alakzat már nincs, azt kell megmutatni, hogy ha e mindkét oldalán szerepel \(\displaystyle {\cal P}\)-beli pont, akkor mindkét oldalon legfeljebb egy szerepelhet, vagyis hogy a (g) alakzat túloldalán már nem szerepelhet pont. Mivel A, E, G kollineáris, az eddig elmondottakat ABC helyett erre a három pontra is alkalmazhatjuk (valójában megcseréltük B-t E-vel és C-t G-vel). Így az AEG egyenes B-t és C-t tartalmazó oldalán sem szerepelhet több pont. Mivel mindegyik eddig kapott alakzatot tartalmazza az A pontban e-re emelt merőleges által meghatározott, C-t tartalmazó félsík, ezért az egész síkon nem lehet több pontja \(\displaystyle {\cal P}\)-nek. \(\displaystyle \square\)

Mostantól legyen \(\displaystyle {\cal P}\) véges, 3-szimmetrikus halmaz, amelynek nincs három kollineáris pontja. Elsőnek a négyszögeket tekintjük át.

5. Állítás. Tegyük fel, hogy \(\displaystyle A,B,C,D\in{\cal P}\) négy különböző pont. Ekkor az ABCD alakzat az alábbiak valamelyike:

(1) egy egyenlő szárú háromszög csúcsai, és a körülírt körének középpontja;

(2) egy rombusz négy csúcsa;

(3) egy szabályos ötszög négy csúcsa.

Ha a négy pont konvex burka háromszög, akkor az első eset áll fenn. Ha négyszög, akkor az (1) és (2) esetben ABCD szimmetrikus bármelyik olyan szögének a szögfelezőjére, amely legalább derékszög.

Bizonyítás. Ismét az 1. Állítást használjuk. Ha A, B, C, D közül valamelyik, mondjuk D az ABC háromszög belsejében van, akkor a D-nél lévő három darab szög (ADB, BDC, CDA) összege 2\(\displaystyle \pi\), és így nem lehet közöttük két hegyesszög. De akkor DA=DB=DC teljesül, és az (1) esetben vagyunk.

Feltehetjük tehát, hogy ABCD egy konvex négyszög, amelynek nincs olyan csúcsa, amely a többi három csúcstól egyenlő távolságra van. Mivel a négyszög valamelyik szöge legalább derékszög, van két szomszédos egyenlő oldal, mondjuk DA=AB=a. Ha a négyszög nem rombusz, akkor feltehető, hogy például BC\(\displaystyle \ne\)a, és mivel az A csúcsból nem indulhat ki három egyenlő szakasz, AC\(\displaystyle \ne\)a. De az ABC háromszög egyenlő szárú, és így AC=BC=b\(\displaystyle \ne\)a. Mivel a C csúcsból sem indulhat ki három egyenlő szakasz, CD\(\displaystyle \ne\)b. Az ACD háromszögben tehát az egyik oldal a, a másik b\(\displaystyle \ne\)a, a harmadik nem b, tehát akkor csak a lehet, vagyis CD=a. A DBC háromszögből tehát BD is a vagy b, de a nem lehet, mert D-ből sem indulhat ki három egyenlő szakasz. Tehát DB=b. A szögeket kiszámolva a szabályos ötszöghöz jutunk.

Végül az utolsó állítás rombuszra nyilvánvaló, ha pedig az alakzat az ABC egyenlő szárú háromszögből, és a köré írt kör O középpontjából áll, ahol AB=BC, akkor a konvexitás miatt ABC tompaszög, és OA=OB=OC miatt az A és C csúcsoknál hegyesszög van. Az O-nál nem biztos, de ez nem baj, mert a négyszög szimmetrikus OB-re. \(\displaystyle \square\)

6. Állítás. A \(\displaystyle {\cal P}\) halmaz vagy konvex helyzetű, vagy egy pontja kivételével egy körön fekszik, és a kivételes pont a kör középpontja.

Bizonyítás. Tegyük fel, hogy az \(\displaystyle O\in{\cal P}\) pont a \(\displaystyle {\cal P}\) konvex burkának belsejében van, és e konvex burok csúcsai \(\displaystyle A_1, \dots,A_n\in{\cal P}\). Az n szerinti indukcióval belátjuk, hogy O mindegyik A_i-től egyenlő távolságra van. Ha n=3, akkor ez az 5. Állításból következik. Tegyük fel, hogy az n-nél kisebb számokra igaz az állítás. Elég belátni, hogy OA₁=OA₂. Tegyük fel, hogy ez nem igaz. Ekkor O nem lehet az A₁A₂A₃ háromszög belsejében (hiszen n=3-ra tudjuk az állítást). Emiatt az A₁A₃A₄...A_n belsejében van, és így az indukciós feltevés miatt O egyenlő távolságra van az A₁,A₃,A₄,...,A_n mindegyikétől. Ezt a gondolatmenetet ismételjük meg az A₁A₃ helyett az A₂A_n átlóval. Ekkor látjuk, hogy az O távolsága A₂,..., A_n-től is ugyanaz. De akkor OA₁=OA_n=OA₂. Ez az ellentmondás bizonyítja az állítást. \(\displaystyle \square\)

7. Állítás. Ha a \(\displaystyle {\cal P}\) halmaz legalább ötelemű, akkor része egy szabályos ötszög csúcsai és a középpontja által alkotott alakzatnak.

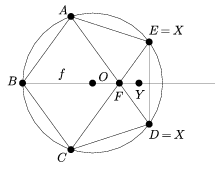
Bizonyítás. Legyenek A, B, C szomszédos csúcsai \(\displaystyle {\cal P}\) konvex burkának úgy, hogy ABC legalább derékszög (ilyen létezik, hiszen a 6. Állítás miatt a konvex burok legalább négyszög). A \(\displaystyle {\cal P}\) halmaznak az A, B, C-n kívül van még legalább két pontja. Mivel az ABC szög f felezőjén (mint minden egyenesen) legfeljebb két \(\displaystyle {\cal P}\)-beli pont lehet, melyek közül B az egyik, van olyan \(\displaystyle X\in{\cal P}\) (és X\(\displaystyle \ne\)A,C), ami nincs ezen a szögfelezőn. Egy ilyen X pont nem lehet az ABC köré írt kör O középpontja (mert O az f-en van). Így a 6. Állítás miatt ABCX konvex négyszög. Mivel ABC legalább derékszög, és X nincs f-en, az 5. Állítás utolsó mondata miatt ABCX egy szabályos ötszög négy csúcsa. Tehát az X pont az ABC háromszöget tartalmazó szabályos ötszög másik két D és E csúcsának valamelyike (vagyis D és E egyike, mondjuk D benne van \(\displaystyle {\cal P}\)-ben). Az előzőek szerint \(\displaystyle {\cal P}\)-nek ezen ötszög csúcsain kívül már csak f-en lehet pontja (a B-n kívül legfeljebb egy). Tegyük fel, hogy Y ilyen pont, azt kell megmutatnunk, hogy Y=O. Ha ez nem igaz, akkor \(\displaystyle O\notin{\cal P}\), és így a 6. Állítás miatt \(\displaystyle {\cal P}\) konvex, vagyis ha F jelöli az AD és CE átlók metszéspontját, akkor Y az F-ből kiinduló, B-t nem tartalmazó félegyenesen lehet csak. De akkor ABY nem egyenlő szárú háromszög (mert ABCF rombusz, amelyben a szögei miatt BA=AF<BF, és így YA és YB is nagyobb, mint AB). Ezzel az állítást és a tételt is beláttuk. \(\displaystyle \square\)

Általánosítások

Természetes módon vetődik fel a kérdés, vajon mit mondhatunk azokról a síkbeli ponthalmazokról, amelyeknek minden négyelemű részhalmaza tengelyesen szimmetrikus. Vagy általánosabban, valamely rögzített k szám mellett megkérdezhetjük, mely ponthalmazok lesznek k-szimmetrikusak, azaz olyanok, hogy bármely k-elemű részhalmazuk tengelyesen szimmetrikus.

Alább következik néhány példa nem-kollineáris, k-szimmetrikus halmazokra, amelyeket - tetszőleges k mellett - némi keresgélés után bárki könnyen megtalálhat. Érezhető, hogy ilyen halmazok kereséséhez úgy érdemes hozzáfogni, hogy a k számot nem tartjuk rögzítve, hanem (először) azt követeljük meg, hogy a keresett ponthalmaz bármely elemét elhagyva a maradék tengelyesen szimmetrikus legyen. Nevezzük az ilyen halmazokat egy híján szimmetrikusnak.

Az alábbi síkbeli ponthalmazok könnyen látható módon mindannyian egy híján szimmetrikusak:

(a) egy szabályos sokszög összes csúcsa;

(a') egy szabályos sokszög összes csúcsa és a középpontja;

(b) egy csúcs kivételével egy szabályos sokszög összes csúcsa;

(b') egy csúcs kivételével egy szabályos sokszög összes csúcsa és a középpontja;

(d) néhány közös középpontú (és különböző méretű) szabályos m-szög és 2m-szög csúcshalmazának egyesítése úgy, hogy a sokszögek rendszerében szereplő m-szögek szimmetriatengelyei közösek (tehát az m-szögek kétféle állásúak lehetnek), és a 2m-szögek csúcsai illeszkednek az m-szögek szimmetriatengelyeire (és így a 2m-szögek csak egyféle állásúak lehetnek);

(d') egy (d) alatt leírt pontrendszer a sokszögek közös középpontjával együtt.

Észrevehetjük, hogy az itt felsorolt ponthalmazok közül az (a) és (a') alattiak kettő híján szimmetrikusak is, azaz bármelyik két pontjukat elhagyva a maradék pontrendszer tengelyesen szimmetrikus.

Van-e még a felsoroltakon kívül véges, nem-kollineáris, egy híján szimmetrikus ponthalmaz a síkon? Bebizonyítható, hogy nincsen. Ennek az igazolását feladat formájában az érdeklődő olvasóra hagyjuk, megtoldva azzal, hogy a kettő híján szimmetrikus halmazokból sem lehet az imént említettektől különbözőt találni.

Feladatok:

(1) Bizonyítsuk be, hogy a sík bármely legalább ötelemű, véges, egy híján szimmetrikus részhalmaza a fenti (a)-(d') példák valamelyike.

(2) Bizonyítsuk be, hogy a sík bármely legalább hatelemű, véges, kettő híján szimmetrikus részhalmaza a fenti (a) és (a') példák egyike.

Ezeket az eredményeket felhasználva könnyen nyerhetünk teljes áttekintést minden k-ra a sík k-szimmetrikus ponthalmazairól. Például rögtön következik az a tétel, hogy k\(\displaystyle \ge\)4 esetén ha egy k-szimmetrikus ponthalmaz legalább (k+3)-elemű, akkor kollineáris.

Érdekes kérdés végül az is, hogy ha az egy híján (vagy kettő híján) szimmetrikus ponthalmazok keresésekor nem korlátozódunk véges halmazokra, milyen újabb példákat kaphatunk. (Ilyenek például egy körvonal vagy egy körlemez összes pontjából, vagy a sík összes racionális koordinátájú pontjából álló halmazok, és még sok más, hasonló módon nyerhető példa.) Ezeknek a halmazoknak az áttekintése és leírása szintén az érdeklődő olvasóra vár.

Kiss Emil¹

Moussong Gábor²

¹A T043671 OTKA támogatásával.

¹A T032478 OTKA támogatásával.

Már regisztráltál?
Új vendég vagy?