A Chladni-féle porábráktól a nanofizikáig
A 2003. évi őszi Ifjúsági Ankéton tartott előadás alapján.

Bevezetés

Napjainkban a fizikai kutatások egyik izgalmas területe a nanofizika. A technológia fejlődésének köszönhetően az anyagban levő elektronokat ma már olyan kicsiny tartományokba sikerült bezárni, melyek mérete néhány nanométer. Ilyen rendszereken végzett kísérletek új kihívásokat teremtettek a kutatók számára. Ezen a mérettartományon a klasszikus fizika törvényei csődöt mondanak, az elektronok viselkedésének leírása csak a kvantumfizika segítségével lehetséges. A múlt század elején kidolgozott kvantumfizika törvényeinek alkalmazása a nanoméretű rendszerekben számos új jelenség felismerésére vezetett az elmúlt 20 évben. Sőt, még ma is további felfedezések várhatók ezen a területen. A kvantumfizika izgalmas kérdéseiről nemrégiben Mihály György professzor úr tartott rendkívül érdekes előadást a Mindentudás Egyetemén, bemutatva egy sor alkalmazást, amelyek alapvető szerepet játszanak mindennapi életünkben.

Több mint 200 évvel ezelőtt, 1787-ben tette közzé első munkáját a német Ernest Florens Friedrich Chladni a rezgő lemezekre szórt homokszemcsék által kirajzolt ábráiról. Édesapja jogásznak szánta fiát, de a jogi diploma megszerzése után Chladni jobban vonzódott a természettudományhoz, és akusztikával, hangtannal kezdett foglalkozni. Eredményeiről számos európai városban tartott előadást, illetve bemutatót. Egyik alkalommal találkozott Napóleonnal is, akinek úgy megtetszettek a különféle porábrák, hogy anyagilag is támogatta Chladni további kutatásait, és 3000 aranyat ajánlott fel annak, aki kielégítő matematikai magyarázatot ad a jelenségre. A díjat végül 1815-ben egy hölgy, Sophie Germain kapta, aki a lemez rezgését differenciálegyenlet segítségével írta le. A kérdéssel számos ismert fizikus is foglalkozott, mint például Kirchhoff, Faraday, Debye és Young. Ma már teljesen tisztázott a lemezek rezgését leíró egyenletek és a kialakuló porábrák szerkezete.

Mi köze a modern fizika egy egészen új területének, a nanofizikának a Chladni-féle porábrákhoz? A fizikának két látszólag igen különböző területéről van szó. A továbbiakban szeretnék rávilágítani erre a kapcsolatra és egyben bemutatni, hogy a nanofizika egyes eredményei hogyan érthetők meg egyszerű analógiák alapján.

A Chladni-féle porábrák

Az 1. ábrán különféle Chladni-lemezek láthatók. Szórjunk egyenletesen vékony rétegben finom homokot vagy krétaport a lemezre. Bizonyos frekvenciával rezgetve a lemezt a homokszemcsék azokra a helyekre gyűlnek össze, ahol a lemez nem mozog, kitérése zérus. Ezeket a helyeket csomóvonalaknak hívják. Az ábrák csak meghatározott, a lemez alakjától, anyagától, méretétől függő frekvenciákon alakulnak ki. Ezeket a frekvenciákat a lemez sajátfrekvenciáinak nevezik. Különböző frekvenciával rezgetett lemezeken érdekes alakú, szerkezetű vonalak alakulnak ki, ahogy ez a 2. ábrán is látható. Ezeket az ábrákat magunk is előállíthatjuk. A lemezt a legegyszerűbben a szélén végighúzott hegedűvonóval hozhatjuk rezgésbe. Az Őszi Ankéton tartott előadáson ezt be is mutattuk. A Chladni-lemezek számos középiskola szertárában megtalálhatók. Az érdeklőknek jó kísérletezést kívánok! Az Eötvös Loránd Tudományegyetemen a tanárszakos hallgatók képzésében ezek a kísérletek kötelező laboratóriumi feladatként szerepelnek.

1. ábra. Különféle Chladni-lemezek

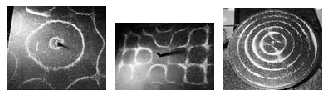
2. ábra. Különböző Chladni-féle porábrák

A vékony lemezek, és a hozzájuk hasonlóan viselkedő, de matematikailag könnyebben kezelhető membránok (hajlékony hártyák) egy adott pontjának kimozdulását (az egyensúlyi állapothoz képest) egy differenciálegyenlettel írhatjuk le. Ez az egyenlet meglehetősen bonyolult, megoldani csak felsőbb matematikai ismeretekkel lehetséges. Az egyenlet alapján kiszámoltuk a lemez kitérését különböző frekvenciákon egy olyan esetben, amikor a kör alakú lemez pereme rögzített. A megoldások a 3. ábrán láthatók, ahol a rezgések egy-egy jellemző pillanatát mutatjuk be. Az első pillanatkép kivételével a többin jól láthatók a kör alakú csomóvonalak. A csomóvonalak alakja, szerkezete függ a lemez alakjától, a rezgés frekvenciájától, illetve attól, hogy hol rögzítjük a lemezt (pl. a 2. ábra jobb szélső képén a kör közepe rögzített, míg a 3. ábrán mutatott esetekben a peremen). Így lehet megvalósítani az ábrák sokféleségét, melyek egy szép gyűjteménye látható egy korabeli könyvben (4. ábra).

3. ábra. Kör alakú membrán kitérése különböző sajátfrekvenciákon. A jó láthatóság kedvéért a kitéréseket erősen felnagyítottuk

4. ábra. Chladni-féle ábrák egy korabeli könyvből

Analógia a membránok rezgése és az elektronok kvantumos viselkedése között

Jelöljük a rezgő membrán egy adott r pontjában és a t időpillanatban a kitérését u(r,t)-vel! Ezt a kitérést a membrán mozgását leíró differenciálegyenlet határozza meg. A membrán csomóvonalait az u(r,t) függvény azon r pontjai adják, melyekre az u kitérés minden időpillanatban zérus.

A kvantumfizikában a mikrorészecskék (például az elektronok) hullámtermészete ma már jól ismert tény. A részecske állapotát egy adott r pontban és t időpillanatban egy \(\displaystyle \psi\)(r,t) hullámfüggvénnyel írhatjuk le. Ennek a hullámfüggvénynek a \(\displaystyle \lambda\) hullámszámát először Louis de Broglie adta meg:

\(\displaystyle \lambda=\frac{h}{p}=\frac{h}{mv}, \)

ahol h=6,62 ^.10^-34 J^.s a Planck-állandó, p=mv az m tömegű és v sebességű részecske (elektron) impulzusa. A \(\displaystyle \psi\)(r,t) hullámfüggvény az ún. Schrödinger-egyenletnek tesz eleget, annak megoldásával határozható meg. A kvantumfizika egyik sajátsága, hogy a részecskének nem lehet egyszerre pontosan meghatározni a helyét és a sebességét (impulzusát). A híres Heisenberg-féle határozatlansági reláció szerint

\(\displaystyle \Delta x\,\Delta p\ge\frac{h}{4\pi}, \)

ahol \(\displaystyle \Delta\)x és \(\displaystyle \Delta\)p a részecske helyének, illetve impulzusának bizonytalansága. Így nincs is értelme a részecskéknek a pályájáról beszélni (pályán általánosan azt értjük, hogy a részecskének mind a helyét, mind a sebességét ismerjük). A kvantumfizikában a részecskének csak a megtalálási valószínűségét határozhatjuk meg, mely a hullámfüggvény abszolút értékének a négyzetével, |\(\displaystyle \psi\)(r,t)|²-tel arányos.

A rezgő membránok u(r,t) kitérését leíró egyenlet és a kétdimenzióban mozgó elektronok \(\displaystyle \psi\)(r,t) hullámfüggvényét meghatározó Schrödinger-egyenlet ugyanolyan alakú differenciálegyenlettel adható meg (ha a rendszer egy sajátfrekvencián rezeg). Ezt az egyenletet az irodalomban Helmholtz-egyenletnek nevezik. A Chladni-lemezek lehetséges kitérése és csomóvonalai lényegében megegyeznek a lemezzel azonos alakú kétdimenziós tartományba zárt elektron hullámfüggvényével és azok csomóvonalaival. A két jelenség közti analógia éppen az őket leíró azonos egyenletből adódik. A következő fejezetben ezt a hasonlóságot használjuk ki a nanofizikában tapasztalt jelenségek megértéséhez.

A fenti áttekintés a kvantumfizikáról meglehetősen rövid, csak azokat az ismereteket kívántam kiemelni, amelyek a továbbiak megértéséhez elengedhetetlenül szükségesek. A kvantumfizika iránt érdeklődő olvasó számára feltétlenül javaslom Károlyházy Frigyes: Igaz varázslat című kitűnő könyvét (Gondolat Kiadó, Budapest, 1976). Ebben a műben a szerző élvezetes módon, középiskolai ismeretek alapján kalauzolja el az olvasót a XX. századi fizika talán legfontosabb szellemi alkotásásába, a kvantumfizikának a rejtelmeibe.

A kvantum-karám

A nanofizikában mérföldkőnek tekinthető az a kísérlet, melyben Crommienak és munkatársainak 1993-ban sikerült vasatomokat előre meghatározott helyre tenni egy rézlapon, és megmérni a rézben lévő elektronok hullámfüggvényét. A vasatomokat ún. pásztázó alagútmikroszkóppal (rövidítése, STM, az angol scanning tunnelling microscope alapján) lehet mozgatni, cipelni a rézlapon egyik helyről a másikra. A pásztázó alagútmikroszkópot Binning és Rohrer találták fel még 1981-ben. Az STM egy hegyes tűből áll (a tű hegyének sugara tipikusan \(\displaystyle 1000~\mbox{\AA}=100~\rm nm\)), mely a vizsgálandó felülettől néhány \(\displaystyle \mbox{\AA}\) távolságban mozgatható (lásd az 5. ábrát). Ha a tűre elektromos feszültséget kapcsolunk, a rajta áthaladó áram ,,átfolyik'' a tűvel szembeni lapra annak ellenére, hogy köztük egy kicsiny rés van. A tűt elhagyó elektronok a kvantumfizika egyik alapvető jelensége, az alagúthatás segítségével juthatnak át a rézlapra. Az elektron hullámfüggvénye ,,átnyúlik'' a tű és a lap közti résen, és így a rézlapon is véges valószínűséggel található az elektron. Az alagútjelenség a mindennapi életünk része. Ennek köszönhető, hogy áramot tudunk átvezetni két drót között akkor is, ha köztük az érintkezés nem tökéletes, esetleg kissé oxidálódott a felületük (pl. a fali konnektorban).

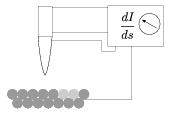
5. ábra. A pásztázó alagútmikroszkóp elvi vázlata

Az STM-et használhatjuk atomok mozgatására egy fémfelületen. Ha a rézlapon lévő vasatom fölé helyezett tű elegendően közel van, akkor nagyobb vonzóerő alakulhat ki a tű és a vasatom között, mint a rézlap és a vasatom között, és így a vasatomot elmozdíthatjuk a rézlapon. A vasatomok mozgatását vázlatosan a 6. ábra szemlélteti. Ezzel a módszerrel helyezték el a rézlapon, kezdetben szétszórtan található 48 darab vasatomot egy \(\displaystyle R=78{,}1~\mbox{\AA}\) sugarú kör mentén. A 7. ábra a kvantum-karám (angolul quantum corral) kiépítésének folyamatát követi nyomon.

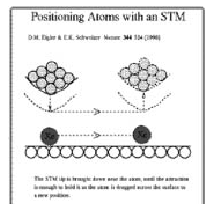
6. ábra. Atomok mozgatása egy fémfelületen

Ugyanakkor az STM-mel feltérképezhetjük a fémfelületet is. Mivel az STM tűje hegyes, a rajta átfolyó áram nagysága a tű alatt elhelyezkedő felület jellegétől függ. Így a tűnek a felületen történő pásztázásával képet, információt kaphatunk magáról a felületről. Kimutatták, hogy a tűn átfolyó áram arányos a felületen lévő elektronok hullámfüggvényének abszolútérték négyzetével, azaz |\(\displaystyle \psi\)(r,t)|²-tel. A tűn áthaladó áram mérésével meghatározhatjuk a felületi elektronok állapotát, a \(\displaystyle \psi\)(r,t) hullámfüggvényt. A rézlap felületén az elektronok jó közelítéssel szabadon mozoghatnak a felület mentén, azaz két dimenzióban. Ezeknek a felületi elektronoknak a száma viszonylag kicsi: minden 12 \(\displaystyle \mbox{\AA}\) élű négyzetben átlagosan egy elektron található. Ugyanakkor a de Broglie hullámhosszuk \(\displaystyle \lambda=29{,}5~\mbox{\AA}\), jóval nagyobb a rézlapban lévő szomszédos rézatomok 2,6 \(\displaystyle \mbox{\AA}\)-ös távolságánál.

7. ábra. Kvantum-karám. 48 darab Fe atom egy \(\displaystyle R=78{,}1~\mbox{\AA}\) sugarú kör mentén

A 7. ábrán kialakított kvantum-karámban a felületi elektronok mozgását csak a körben elhelyezkedő vasatomok befolyásolják. Gyakorlatilag a vasatomok az elektronokat egy kétdimenziós, nanométeres méretű tartományba zárják be. Ezeknek a felületi elektronoknak a lehetséges állapotai, a \(\displaystyle \psi\)(r,t) hullámfüggvényük az előző fejezetben tárgyalt analógia alapján megegyeznek a Chladni-lemezek lehetséges elmozdulás-függvényeivel, melyeket korábban az 3. ábrán láttunk. A 8. ábrán az STM-mel kimért felületi elektronok \(\displaystyle \psi\)(r,t) hullámfüggvénye látható (http://www.nanoscience.com/education/STM.html). Az ábrán jól felismerhetők a kör alakú csomóvonalak, ahogy ez a Chladni-féle porábrákon is megfigyelhető. Ez a kísérleti eredmény jól bizonyítja a hasonlóságot a Chladni-lemezek rezgési állapotai és a nanométeres tartományba zárt elektronok állapotai között.

8. ábra. A rézben lévő felületi elektronok hullámfüggvénye az előző ábrán bemutatott, kísérletileg létrehozott kvantum-karámban. A kör mentén a hegyes tűszerű kiemelkedések a vasatomok mikroszkópos képei

Nem csak kör alakú kvantum-karámokat lehet ,,építeni''. A 9. ábrán egy stadion alakú tartományba zárt elektron hullámfüggvényének STM-mel mért képe látható (http://www.aip.org/physnews/graphics/html/corral.htm ). A Helmholtz-egyenlet megoldásával elméletileg is meghatározták a lehetséges kvantumállapotokat. A 10. ábrán jól látható az egyezés a kísérletileg mért és elméletileg számolt hullámfüggvény között. Ezek a kutatási eredmények alapvetően fontosak, hiszen közelebb visznek a jelenségek pontosabb megértéséhez.

9. ábra. Stadion alakú kvantum-karám és az elektron hullámfüggvénye

10. ábra. Stadion alakú kvantum-karámba zárt elektron kísérletileg és elméletileg meghatározott hullámfüggvényének összehasonlítása. A bal oldalon az elméleti, jobb oldalon a kísérleti eredmény látható

A fenti kísérletek megvalósítását komoly mérnöki problémák leküzdése előzte meg. Ki kell zárni, de legalábbis minimálisra kell csökkenteni a különféle zavaró rezgéseket. A kísérletek nagy vákuumban folynak. A hőmozgások elkerülése érdekében viszonylag alacsony hőmérsékleten, tipikusan 70 K alatt történik a mérés. Komoly elektronikai és számítógépes vezérlésekre van szükség. Hogy benyomást szerezzünk arról, milyen technikai feladatok megoldására van igény a nanofizikában, vessünk egy pillantást a 11. ábrára, ahol a kísérleti berendezés látható. A nanofizikai kutatásokhoz nélkülözhetetlen a magas szintű technológia alkalmazása.

11. ábra. A pásztázó alagútmikroszkóp kísérleti berendezése

A nanoméretű tartományokban kialakuló kvantumállapotok tanulmányozása a fizika egy új területének, a nanofizikának kialakulásához vezetett. Lehetőség nyílt a kvantumfizika törvényszerűségeit behatóbban kutatni, illetve új jelenségeket felfedezni. A nanofizika eddigi rohamos fejlődése során számos új eredmény született, melyek ígéretes alkalmazási lehetőségekkel kecsegtetnek. Ezen alapkutatási eredmények közül több is szokatlanul gyorsan, néhány év után beépült a mindennapi életünkbe. Biztosak lehetünk abban, hogy a nanofizika újabb kihívásai sok-sok izgalmas kutatási témát adnak a jövőben is a fizikusok számára.

Köszönetemet szeretném kifejezni Bérces Györgynek, aki segítségemre volt az előadásomon bemutatott Chladni-féle porábrák demonstrációjának előkészületeiben, Hatta Gizellának, Geszti Tamásnak és Pollner Péternek a kézirat olvasása után javasolt hasznos tanácsaikért, valamint hallgatómnak Oroszlány Lászlónak, aki segítségemre volt az 3. ábra elkészítésében.

Cserti József
ELTE Komplex Rendszerek Fizikája Tanszék