A Feuerbach-kör érinti az érintő köröket¹

Két bizonyítást ismertetünk Feuerbach fenti tételére.

Jelölések

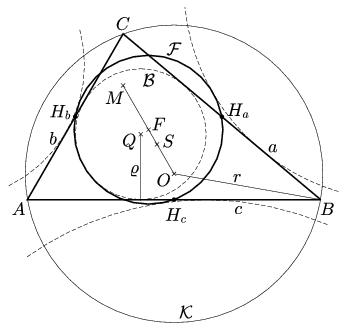
Az ABC háromszög három oldalát jelölje a, b és c a szokásos módon. Jelölje $\displaystyle \mathcal{K}$ a körülírt kört, középpontja O, sugara r, $\displaystyle \mathcal{B}$ a beírt kört, középpontja Q, sugara $\displaystyle \varrho$, és legyen a háromszög területe t, félkerülete s, súlypontja S, magasságpontja M, az oldalak felezőpontjai H_a, H_b és H_c. A Heron formula kifejezi a háromszög területét az oldalhosszakkal,

$\displaystyle t=\sqrt{s(s-a)(s-b)(s-c)}. $

További ismert területképletek:

$\displaystyle t=\varrho s=\frac{1}{2}ab\sin\gamma=\frac{abc}{4r}. $

Ezekből és a Heron képlet kifejtéséből kapjuk, hogy

(1)	$\displaystyle 2r\varrho=\frac{abc}{a+b+c}, $

(2)	$\displaystyle \varrho^2=\frac{(s-a)(s-b)(s-c)}{s}= $

$\displaystyle {}=\frac{-a^3-b^3-c^3-2abc+ab^2+ac^2+ba^2+bc^2+ca^2+cb^2}{4(a+b+c)}. $

1. ábra

A Feuerbach-kör

Jelölje $\displaystyle \mathcal{F}$ a háromszög oldalfelező pontjain átmenő kört. Mivel a H_aH_bH_c háromszöget az ABC-ből az S centrumú és $\displaystyle -\frac{1}{2}$ arányú kicsinyítéssel kaphatjuk, az $\displaystyle \mathcal{F}$ sugara $\displaystyle \frac{r}{2}$ és centruma, F, rajta van a háromszög Euler egyenesén: F az OM szakasz felezőpontja, S harmadolja OM-et es OF-et. Euler (1707-1783) is tudta, hogy $\displaystyle \mathcal{F}$ átmegy a magasságok talppontjain és az M-et a csúcsokkal összekötő szakaszok felezőpontjain. Ami miatt $\displaystyle \mathcal{F}$-et mégis Feuerbach körnek hívjuk, az a következő szép tétel:

Tétel. $\displaystyle \mathcal{F}$ érinti a beírt kört és a hozzáírt köröket.

Karl Wilhelm Feuerbach (1800-1834) 1822-ben doktori disszertációjában a szóban forgó körök középpontjainak távolságát számolta ki. Megmutatta, hogy $\displaystyle |FQ|= \left|\frac{1}{2}r-\varrho\right|$. Mivel a háromszög minden adata kifejezhető a, b, c-vel, ha másképp nem, legalább implicit módon egy egyenlet(rendszer) gyökeként, ez a számolás elvileg elvégezhető. Ha az A, B, C pontokat egy koordinátarendszer (0;0), (1;0) és (x;y) pontjaiba tesszük, akkor csak két paraméterrel kell számolnunk. Az egymásra épülő mennyiségek kiszámítása azonban egyre magasabb fokú egyenlethez vezethet, amit egyre nehezebb kezelni. Ezért az tétel legtöbb bizonyítása vektorokat használ. Az alább ismertetett számolás viszonylagos rövidségével tűnik ki. A gondolatmenet lényegesebb elemeit (1. lemma) több mint 30 évvel ezelőtt Reiman István feladatmegoldó szakkörén tanultam és elolvasható Reiman István: Geometria és határterületei c. könyvében (Gondolat Kiadó, Budapest, 1986).

Kényelmesebb a távolságok négyzetének meghatározása, ezzel elkerülhető a gyökvonás, csupán racionális törtfüggvények jönnek elő. Az (1)-ből és (2)-ből máris ismerjük az $\displaystyle \left(\frac{1}{2}r-\varrho\right)^2=\frac{1}{4}r^2-r\varrho+\varrho^2$ utolsó két tagját a, b, c-vel kifejezve. Az alábbiakban az |FQ|² kiszámításakor csupán a, b, c és r szerepel.

Vektorok

Sokat egyszerűsíthet a koordinátarendszer centrumának szerencsés megválasztása. Esetünkben jelölje az O pontból az X-be vezető vektort X. Ekkor |A|= |B|= |C|=r. Bármely centrum esetén $\displaystyle \mathbf{S}= \frac{1}{3}(\mathbf{A}+\mathbf{B}+\mathbf{C})$. Mivel a helyvektorok kezdőpontja O és az O, S, M és F pontok az Euler egyenesen vannak, kapjuk, hogy M=3S=A+B+C és

(3)	$\displaystyle \mathbf{F}=\frac{1}{2}(\mathbf{A}+\mathbf{B}+\mathbf{C}). $

1. lemma.

(4)	$\displaystyle \mathbf{Q}=\frac{a\mathbf{A}+b\mathbf{B}+c\mathbf{C}}{a+b+c}. $

Bizonyítás. Jelölje P a (4) jobb oldalán álló törtet. Belátjuk, hogy a végpontja rajta van a szögfelezőkön. A C-A vektor hossza b, így $\displaystyle \frac{1}{b} (\mathbf{C}-\mathbf{A})$ az A-ból C felé mutató egységvektor. Hasonlóképp $\displaystyle \frac{1}{c}(\mathbf{B}-\mathbf{A})$ a B-felé mutató egységvektor. E kettő összege, azaz $\displaystyle \frac{b\mathbf{B}+c\mathbf{C}-(b+c)\mathbf{A}}{bc}$ végpontja az A-ból induló szögfelezőn van. A szögfelező egyenes bármely pontját megkaphatjuk, ha ezen összeg egy skalárszorosát az A-hoz adjuk. A törtektől megszabadulva kapjuk az A-n átmenő belső szögfelező paraméteres vektoregyenletét:

f_A (x)= A+ x (bB+ cC- (b+c)A).

Ha x végigfut a valós számokon, az f_A(x) vektorok a szögfelező pontjait adják. Az eredmény ismeretében könnyű az ellenőrzés, az f_A(x) alkotta egyenest két pontja meghatározza: x=0 az A csúcspontot adja, $\displaystyle x=\frac{1}{b+c}$ a BC szakasz azon pontját, amely azt c:b arányban osztja, azaz a szögfelező talppontját. Az $\displaystyle x= \frac{1}{a+b+c}$ értéket választva látjuk, hogy P rajta van a szögfelezőn. P rajta van a többi szögfelezőn is, így szükségképpen P=Q. $\displaystyle \square$

A legegyszerűbb vektortulajdonságokon kívül (összeadás kommutativitása, lineáris kombináció) szükségünk lesz a skalárszorzat fogalmára. Mivel egy vektor önmagával vett szorzata a hossz négyzete, egy tetszőleges |XY| távolság, illetve a négyzete így számolható: |XY|²= |X- Y|²= X²+ Y²-2X Y. A skalárszorzat kommutativitásán és bizonyos asszociativitásán kívül csak az AB, AC és BC szorzatok értéket használjuk. Mivel c²= |B-A|²= |B|²+|A²|- 2AB= 2r²-2AB, kapjuk, hogy

(5)	$\displaystyle \mathbf{A}\mathbf{B}=r^2-\frac{1}{2}\,c^2,\quad\mathbf{A}\mathbf{C}=r^2-\frac{1}{2}\,b^2, \quad\mathbf{B}\mathbf{C}=r^2-\frac{1}{2}\,a^2. $

A tétel bizonyítása. Számoljuk ki a két középpont, F és Q távolságát.

(6)	$\displaystyle \mathbf{Q}^2={\|\mathbf{Q}\|}^2= \left(\frac{a\mathbf{A}+b\mathbf{B}+c\mathbf{C}}{a+b+c}\right)^{2}=$

$\displaystyle =\frac{a^2\mathbf{A}^2+b^2\mathbf{B}^2+c^2\mathbf{C}^2+ 2ab\mathbf{A}\mathbf{B}+2ac\mathbf{A}\mathbf{C}+2bc\mathbf{B}\mathbf{C}}{{(a+b+c)}^2}= $

$\displaystyle =\frac{a^2r^2+b^2r^2+c^2r^2+2abr^2-abc^2+2acr^2-acb^2+2bcr^2-bca^2}{{(a+b+c)}^2}= $

$\displaystyle =r^2-\frac{abc}{a+b+c}. $

Ebből (1) adja Euler tételét, hogy

(7)	\|Q\|²= r²-2r$\displaystyle \varrho$

és ebből $\displaystyle \frac{1}{2}\,r\geq\varrho$.

(8)	$\displaystyle \mathbf{F}^2={\|\mathbf{F}\|}^2=\frac{1}{4}{(\mathbf{A}+\mathbf{B}+\mathbf{C})}^2= \frac{1}{4}(3r^2+2\mathbf{A}\mathbf{B}+2\mathbf{A}\mathbf{C}+2\mathbf{B}\mathbf{C})= $

$\displaystyle =\frac{1}{4}(9r^2-a^2-b^2-c^2), $

(9)	$\displaystyle 2\mathbf{F}\mathbf{Q}=(\mathbf{A}+\mathbf{B}+\mathbf{C}) \frac{a\mathbf{A}+b\mathbf{B}+c\mathbf{C}}{a+b+c}=$

$\displaystyle =\frac{1}{a+b+c}\big(a\mathbf{A}^2+b\mathbf{B}^2+c\mathbf{C}^2+(a+b) \mathbf{A}\mathbf{B}+(a+c)\mathbf{A}\mathbf{C}+(b+c)\mathbf{B}\mathbf{C}\big)= $

$\displaystyle =r^2+\frac{1}{a+b+c}\bigg((a+b)\left(r^2-\frac{1}{2}c^2\right)+(a+c) \left(r^2-\frac{1}{2}b^2\right)+ $

$\displaystyle \quad+(b+c)\left(r^2-\frac{1}{2}a^2\right)\bigg)= $

$\displaystyle =3r^2-\frac{1}{2(a+b+c)}(ac^2+bc^2+ab^2+cb^2+ba^2+ca^2). $

A (6), (8) egyenletek összegéből vonjuk le a (9)-et:

$\displaystyle {|\mathbf{F}-\mathbf{Q}|}^2=\mathbf{F}^2+\mathbf{Q}^2-2\mathbf{F}\mathbf{Q}=\frac{1}{4}r^2+ $

$\displaystyle +\frac{-4abc-(a+b+c)(a^2+b^2+c^2) +2(ac^2+bc^2+ab^2+cb^2+ba^2+ca^2)}{4(a+b+c)}= $

$\displaystyle =\frac{1}{4}r^2-\frac{2abc}{4(a+b+c)} +\frac{-a^3-b^3-c^3-2abc+ab^2+ac^2+ba^2+bc^2+ca^2+cb^2}{4(a+b+c)}. $

Ebből (1) és (2) felhasználásával adódik, hogy

$\displaystyle {|\mathbf{F}-\mathbf{Q}|}^2=\frac{1}{4}r^2-r\varrho+\varrho^2= \left(\frac{1}{2}r-\varrho\right)^{2}. $

Az FQ szakasz hossza tehát $\displaystyle \frac{1}{2}r-\varrho$, és így a Q középpontú $\displaystyle \varrho$ sugarú kör belülről érinti az F középpontú $\displaystyle \frac{1}{2}r$ sugarú kört (a Feuerbach kört). $\displaystyle \square$

Megjegyzések

1. Lássuk be, hogy az a oldalhoz hozzáírt kör középpontjába mutató vektor

$\displaystyle \mathbf{Q}_a=\frac{-a\mathbf{A}+b\mathbf{B}+c\mathbf{C}}{-a+b+c}. $

2. Készítsünk a fentiekhez hasonló bizonyítást arra, hogy a beírt kör kívülről érinti a hozzáírt köröket!

3. Jean-Victor Poncelet (1788-1867) tétele szerint ha egy k oldalú A₁, ...,A_k poligon csúcsai egy $\displaystyle \mathcal{K}$ körön vannak és egyidejűleg oldalai egy $\displaystyle \mathcal{B}$ kört érintenek, akkor a $\displaystyle \mathcal{K}$ tetszőleges X=X₁ pontjából kiindulva a $\displaystyle \mathcal{B}$-hez érintőt húzva és így a $\displaystyle \mathcal{K}$-ból a következő, X₂ pontot nyerve, majd ezen eljárást folytatva a k-adik lépés után a kapott töröttvonal záródik, X_k+1=X₁.²

Az Euler formulára (7) támaszkodva, lássuk be Poncelet tételét a k=3 esetre!

4. Az 1. lemmához hasonló tétel (lényegében ugyanolyan egyszerű bizonyítással) minden dimenzióban igaz, pl. ha A₁, A₂, A₃, A₄ egy tetraéder csúcsai, és A₁, A₂, A₃, A₄ a köréírt gömb középpontjából odamutató helyvektorok, és Q a beírt gömb középpontjába, Q-ba mutató helyvektor, akkor

$\displaystyle \mathbf{Q}=\sum_{1\leq i\leq4}\frac{t_i}{t_1+\dots+t_4}\mathbf{A}_i, $

ahol t_i az A_i-vel szemközti lap területe.

5. A (8) egyenletet használva bizonyítsuk, hogy sin² $\displaystyle \alpha$+ sin² $\displaystyle \beta$+sin²$\displaystyle \gamma$=2 akkor és csak akkor, ha a háromszög derékszögű.

6. Igazoljuk, hogy az $\displaystyle \mathcal{F}$ Feuerbach kör érinti az ABM, ACM es BCM háromszögek beírt és hozzáírt köreit is. (Ez további 12 kör!)

Bizonyítás inverzióval

Ismertetjük a Feuerbach tétel legegyszerűbb bizonyítását, amelyet egymástól függetlenül M'Clelland (1891) és Lachlan (1893) talált, és amelyet a legtöbb tankönyv átvett (pl. D. Pedoe: Circles, MAA publication, 1957, 1979, 1995). A fő gondolat (a 2. lemma) alábbi bizonyítása új, a szokásosnál valamelyest egyszerűbb.

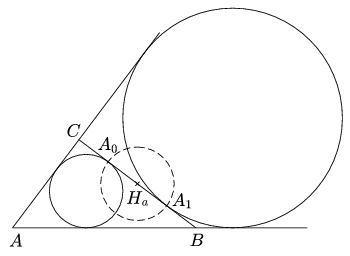
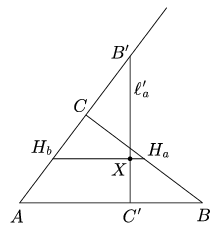
Jelölje A₀ az a oldalon a $\displaystyle \mathcal{B}$ beírt kör érintési pontját, jelölje A₁ az a oldalhoz hozzáírt $\displaystyle \mathcal{H}$ kör érintési pontját, és jelölje f e két kör közös szimmetriatengelyét, az A ponton átmenő belső szögfelezőt. E két körnek 4 közös érintője van, az $\displaystyle \ell$_a, $\displaystyle \ell$_b, $\displaystyle \ell$_c oldalegyenesek, és egy negyedik $\displaystyle \ell$_a' egyenes, amely az $\displaystyle \ell$_a tükörképe f-re. Legyen B' és C' a B és C csúcs f-re vonatkozó tükörképe, ekkor B', C'$\displaystyle \in$ $\ell$ _a'.

Mivel |CA₀|=s-c és |BA₁|=s-c, az A₀A₁ szakasz felezőpontja H_a és hossza |a-2(s-c)|=|c-b|. Tegyük fel, hogy b $\ne$ c és jelölje i az A₀A₁ átmérőjű körre vonatkozó inverziót. Ekkor i(A₀)=A₀, i(A₁)=A₁, i( $\ell$ _a)= $\ell$ _a.

2. ábra

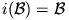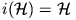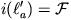2. lemma. $i({\mathcal{B}})={\mathcal{B}}$ , $i({\mathcal{H}})={\mathcal{H}}$ és $i(\ell_a')= {\mathcal{F}}$ .

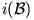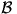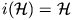Bizonyítás. Az inverzió megtartja az érintkezést, így $i(\mathcal{B})$ érinti i( $\ell$ _a)-t az i(A₀) pontban. Kapjuk, hogy $\mathcal{B}$ képe önmaga. Hasonlóképp adódik, hogy $i(\mathcal{H})=\mathcal{H}$ .

3. ábra

Azt kell még bizonyítanunk, hogy 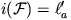$i(\mathcal{F})=\ell_a'$ . Mivel 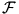$\mathcal{F}$ tartalmazza az inverzió centrumát, H_a-t, így képe egy egyenes. Belátjuk, hogy H_b és H_c képei az $\ell$ _a' egyenesre kerülnek. Tekintsük H_b-t, a H_c esete analóg. Legyen X a H_aH_b és $\ell$ _a' egyenesek metszéspontja. A B'AC' és B'H_bX háromszögek hasonlósága adja, hogy

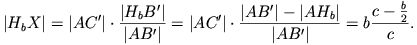
$|H_bX|=|AC'|\cdot\frac{|H_bB'|}{|AB'|}=|AC'|\cdot\frac{|AB'|-|AH_b|}{|AB'|}=b \frac{c-\frac{b}{2}}{c}.$

Ha itt 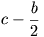$c-\frac{b}{2}$ negatív, akkor X a [H_bH_a] szakaszon kívül van. Kapjuk, hogy 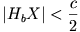$|H_bX|<\frac{c}{2}$ és így X a [H_aH_b) félegyenesre kerül. Továbbá

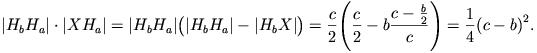
$|H_bH_a|\cdot|XH_a|=|H_bH_a|\big(|H_bH_a|-|H_bX|\big)=\frac{c}{2} \Bigg(\frac{c}{2}-b\frac{c-\frac{b}{2}}{c}\Bigg)=\frac{1}{4}{(c-b)}^2.$

Tehát i(H_b)=X, így i(H_b) $\in$ $\ell$ _a'. $\square$

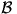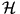Végül, mivel az $\ell$ _a' a $\mathcal{B}$ és $\mathcal{H}$ közös érintője, így 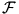$\mathcal{F}$ közös érintő (köre) ezen körök képének. Mivel 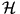$\mathcal{H}$ helyett más hozzáírt kör is állhat, így 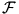$\mathcal{F}$ mind a négy érintő kört érinti.

Appendix, az inverzió néhány tulajdonsága

Az O középpontú r sugarú körre vonatkozó i inverzió a sík O-n kívüli pontjainak egy bijekciója úgy, hogy a P pont i(P) képe rajta van az O-ból induló, P-n átmenő félegyenesen, és |OP|^.|O i(P)|=r². Ez egy involúció, azaz i(i(P))=P.

- Egy O-n átmenő $\ell$ egyenes képe önmaga (pontosabban 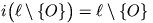$i\big(\ell\setminus\{O\}\big)=\ell\setminus\{O\}$ .)

- Ha 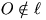$O\notin\ell$ , akkor képe egy O-n átmenő kör.

- Egy O-t tartalmazó kör képe egy, az O-t elkerülő egyenes.

- Egy O-t elkerülő kör képe egy másik kör, külső hasonlóságpontjuk O.

- Az inverzió megtartja az érintést, érintő egyenesek és körök képe érinti egymást. (Valójában több is igaz, az inverzió szögtartó).

Füredi Zoltán

¹ Research supported in part by the Hungarian National Science Foundation under grants OTKA T 032452, T 037846 and by the National Science Foundation under grant DMS 0140692.

² Poncelet tételéről lásd Hraskó András cikkét a KöMaL 2000. évi 5. számában.

Már regisztráltál?
Új vendég vagy?