Hiperbolikus Escher-grafikák
A híres holland grafikus, Maurits Cornelis Escher (1898-1972) sokféle matematikai témát feldolgozott. Közismertek például azok a metszetei, amelyeken több irányban is periodikus minták ismétlődnek. Ezeken pontosan egymáshoz illeszkedő mintázatok töltik ki a képet. Vannak olyan művei is, amelyeket egyetlen alakzat tükörképeiből szerkesztett.
Escher 1958-ban ismerkedett meg és került barátságba a híres geométerrel, Donald Coxeterrel, akinek a Poincaré-féle körmodellről írt cikke keltette fel a művész érdeklődését a körmodell csempézései iránt. Több olyan fametszetet is készített - a híres Circle Limit sorozatot -, amelyen a körmodellt csempézte ki periodikus mintákkal. Coxeter elismeréssel nyilatkozott a művekről, amelyek aprólékos pontossággal követték a geometria előírásait.
Számítógép segítségével nem nehéz Escher-szerű képeket készíteni. A számítógép gyorsan és pontosan végrehajthatja a szerkesztéseket. A minta kitalálásában persze nem segít, ez a mi feladatunk. Az interneten több olyan oldal található [8, 9, 10], ahol Escher-szerű grafikákat készíthetünk az euklideszi síkon; nekünk csak a mintát kell lerajzolnunk, a csempézést a számítógép készíti el. De a hiperbolikus sík különböző modelljeinek ,,Circle Limit szerű'' csempézéseit is elkészíthetjük.
E cikken belül nem vállalkozhatunk az összes elhangzó fogalom definiálására, ugyanakkor a matematikában jártasabb Olvasóink kedvéért szeretnénk rámutatni a téma és a geometria más ágai közötti kapcsolatokra. Ezért előfordulnak olyan matematikai kifejezések, amelyek sokak számára ismeretlenek lehetnek; ezekhez mindig mutatunk forrásokat - könyveket, cikkeket -, ahol az Olvasó utána járhat, de a cikk megértésében az sem okoz problémát, ha ezeket az első elolvasáskor egyszerűen átugorja.
A hiperbolikus sík és néhány modellje
A párhuzamossági axióma bizonyítási kísérletei vezettek el a 19. század első harmadában a ,,hiperbolikus'' geometria felfedezéséhez. Bolyai János és Nyikoláj Ivanov Lobacsevszkij egymástól függetlenül építette fel és publikálta a hiperbolikus geometria legfontosabb tulajdonságait. (Bolyai küzdelméről eredményei elismeréséért bővebben olvashatunk Reiman István könyvében [6c].)
A hiperbolikus sík részletes tárgyalása több tankönyvfejezet témája. Az érdeklődő Olvasó figyelmébe ajánljuk a már említett Reiman-könyvön kívül Coxeter tankönyvét [1b] és Surányi László interneten található Bolyai-gyűjteményét [7]. Most csak azokat a legfontosabb ismereteket szeretnénk összefoglalni, amelyekre a hiperbolikus grafikák készítéséhez szükségünk lesz.
A hiperbolikus síkon ugyanazok az axiómák igazak, mint az euklideszi síkon, kivéve a párhuzamossági axiómát, amelynek a tagadása szerepel:
Ha e a sík tetszőleges egyenese és P egy azon kívüli tetszőleges pont, akkor P-n keresztül végtelen sok olyan egyenes húzható, aminek nincs közös pontja e-vel.
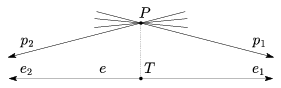
2. ábra. A párhuzamossági axióma tagadása
Az e-t nem metsző (fél)egyenesek között van két ,,szélső helyzetű''; az ábrán ezeket jelöltük p1-gyel, illetve p2-vel. Ezeket az e egyenessel, illetve az e1 és e2 félegyenesekkel párhuzamosnak, a többi nem metsző egyenest pedig ultraparalelnek hívjuk.
Természetesen a hiperbolikus síkon is mérünk távolságokat és szögeket. Lényeges különbség, hogy nem találkozunk a hasonlóság jelenségével; ha két háromszögnek ugyanazok a szögei, akkor egybevágók. A háromszögek szögösszege mindig határozottan kisebb, mint 180o, és általában a sokszögek szögösszege kisebb, mint az euklideszi esetben.
A hiperbolikus sík struktúrája nem teljesen egyértelmű. Ha más távolságot választunk egységnek - azaz a távolságokat ugyanazzal a számmal megszorozzuk, átskálázzuk -, a struktúra megváltozik; például az ugyanolyan hosszú oldalakkal szerkesztett háromszög szögei mások lesznek. Ezért a hiperbolikus síknak van egy paramétere, egy pozitív valós szám, ami a skálázást írja le. Ezt a paramétert többnyire k-val szokás jelölni.
A szögösszeg hiányának, a defektusnak érdekes geometriai jelentése van; szoros kapcsolatban áll a területtel. Ha egy háromszög szögei - ívmértékben mérve - \(\displaystyle \alpha\), \(\displaystyle \beta\) és \(\displaystyle \gamma\), akkor a háromszög területe k2.(\(\displaystyle \pi\)-\(\displaystyle \alpha\)-\(\displaystyle \beta\)-\(\displaystyle \gamma\)). Általában, egy sokszög területe a szöghiány k2-szerese - éppen úgy, mint ahogy a gömbsokszögek területe a szögtöblettel arányos.
Az euklideszi síkon és térben sokféle struktúrát ismerünk, amire teljesülnek a hiperbolikus sík axiómái. Ezekben a struktúrákban nem ugyanazokat a geometriai objektumokat nevezzük pontnak és egyenesnek, és másképpen mérünk távolságokat és szögeket.
A modelleknek nagy jelentősége van az úgynevezett relatív ellentmondásmentességi bizonyításokban. Ha az euklideszi axiómák ellentmondásmentesek, akkor az euklideszi geometriában konstruált modell léte bizonyítja, hogy a hiperbolikus sík is lehetséges és a párhuzamossági axióma nem következik a többi euklideszi axiómából.
A továbbiakban négy modellt mutatunk be. Mindegyik modellben definiáljuk, hogy mik a pontok és az egyenesek, definiáljuk a távolságot és a szögeket. A bemutatott modellek közül a Cayley-Klein modellről és a Poincaré-féle körmodellről már olvashattunk például Hraskó András cikkében [8].
A Cayley-Klein modell
Vegyünk az euklideszi síkon egy kört (alapkör). A kör belsejébe eső pontok lesznek a modell pontjai, a kör húrjai pedig az egyenesek. Két (fél)egyenes akkor párhuzamos, ha a végpontjuk közös (3. ábra).
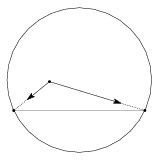
3. ábra. Párhuzamosok
A Cayley-Klein modellben fontos szerepet játszanak a projektív geometria [3b, 6b] különféle eszközei. Például az egybevágósági transzformációk az euklideszi síknak azok a projektív transzformációi (kollineációi), amelyek az alapkört, illetve annak belsejét önmagára képezik. Az alapkörre vonatkozó polaritás [3c, 5] is kiemelt szerepet játszik: két egyenes pontosan akkor merőleges a modellben, ha konjugáltak (4. ábra).
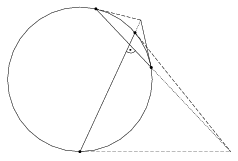
4. ábra. Merőlegesség
A távolságot a kettősviszony [3b, 6a] logaritmusaként definiáljuk. Ha X, Y két pont az alapkör AB húrján (4. ábra), akkor az X és Y pontok távolsága
| (1) | \(\displaystyle d(X,Y)=\frac{k}2\cdot\big|\ln(ABXY)\big|=\frac{k}2\cdot\left|\ln\frac{AX}{XB}: \frac{AY}{YB}\right|. \) |
Az alapkör középpontjában a szögek megegyeznek az euklideszi szögekkel. A középponttól különböző csúcsú szögek definíciója bonyolultabb, később visszatérünk rá.
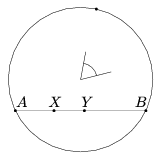
5. ábra. Távolság és szög
1. feladat. Legyen X, Y, Z három, ilyen sorrendben egy egyenesre eső pont. Ellenőrizzük, hogy d(X,Y)+d(Y,Z)=d(X,Z).
A Poincaré-féle körmodell
A körmodellben ismét egy alapkör belseje a sík, de az egyenesek definíciója lényegesen különbözik. A modellbeli egyenesek az átmérők, valamint az alapkört merőlegesen metsző köröknek az alapkör belsejébe eső ívei. Két (fél)egyenes ezúttal is akkor párhuzamos, ha a végpontjuk az alapkörnek ugyanaz a pontja (6. ábra).
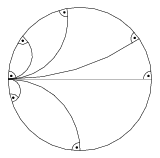
6. ábra. Párhuzamosok
Ha X, Y két pont az alapkörre merőleges AB köríven (7. ábra), akkor az X és Y pontok távolsága
| (2) | \(\displaystyle d(X,Y)=k\cdot\big|\ln(ABXY)\big|=k\cdot\left|\ln\frac{AX}{XB}: \frac{AY}{YB}\right|. \) |
(A képletben négy, egy körön fekvő pont kettősviszonya szerepel, ami pontosan ugyanúgy fejezhető ki a húrok hosszával, mint amikor egy egyenesre esnek.)
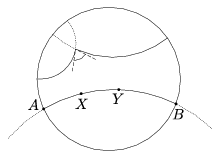
7. ábra. Távolság és szög
A szögek definíciója nagyon egyszerű: két egyenes (körív) bezárt szöge megegyezik a körívek metszéspontjában húzott érintők euklideszi szögével (7. ábra).
A körmodell geometriája szorosan kapcsolódik az inverzióhoz és az inverzív síkhoz [1a, 2, 3a]. A tengelyes tükrözés például nem más, mint a tengelyt reprezentáló körre történő inverzió. Általában az egybevágósági transzformációk az inverzív síknak azok a körtartó transzformációi, amelyek az alapkör belsejét önmagára képezik.
2. feladat. Legyen X, Y, Z három, ilyen sorrendben egy egyenesre eső pont. Ellenőrizzük, hogy a körmodellben is d(X,Y)+d(Y,Z)=d(X,Z).
3. feladat. Legyen P a körmodell egy pontja, amely nem esik egybe a modell középpontjával. A P-n átmenő hiperbolikus egyeneseket (köríveket) hosszabbítsuk az alapkörön túl. Igazoljuk, hogy a meghosszabbításoknak is van egy közös P' pontja az alapkörön kívül. Mi a geometriai kapcsolat P és P' között?
4. feladat. Legyen P és Q a körmodell két különböző pontja. Szerkesszük meg körzővel és vonalzóval a P-n és Q-n átmenő hiperbolikus egyenest.
5. feladat. Igazoljuk, hogy a körmodellben a körök euklideszi értelemben is körök.
6. feladat. Mutassunk a körmodellben olyan háromszöget, amelynek nincs körülírt köre!
A Poincaré-féle félsíkmodell
A körmodellből inverzióval további modelleket kaphatunk. Válasszunk ki az alapkörön egy P pontot, és alkalmazzunk a modell minden pontjára egy P pólusú inverziót. Az alapkör képe egy egyenes lesz, a kör belsejének képe pedig egy F nyílt félsík. Azoknak a hiperbolikus egyeneseknek a képe, amiknek egyik vége P, egy-egy félegyenes lesz, amelyek merőlegesek F határára; azoknak a képe pedig, amiknek egyik vége sem P, egy-egy félkör (8. ábra).
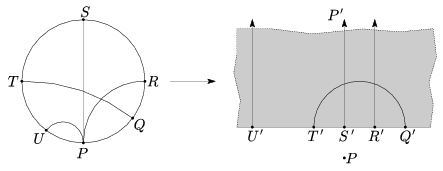
8. ábra. A körmodell és a félsíkmodell kapcsolata
A félköröket és félegyeneseket egységesen is kezelhetjük az inverzív síkon, ha a félegyeneseket olyan félkörökként kezeljük, amelyeknek másik végpontja az ideális (végtelen távoli) pont.
A szögeket és távolságokat ugyanúgy mérjük, mint a körmodellben. Két, egymást metsző félkör bezárt szöge megegyezik az érintők euklideszi szögével. Ha pedig X és Y két pont az AB félkörön, akkor a távolságukat most is a (2) képlettel definiálhatjuk. Abban az esetben, ha X és Y egy félegyenesre esik, azaz például B az ideális pont, akkor a \(\displaystyle \frac{BX}{BY}\) hányadost 1-nek tekintjük és
\(\displaystyle d(X,Y)=k\cdot\left|\ln\frac{AX}{AY}\right|. \)
7. feladat. Legyenek az A, B, C, D pontok egy körön vagy egy egyenesen ebben a sorrendben. Alkalmazzunk egy inverziót ezekre a pontokra; a képük legyen A', B', C', D'. Igazoljuk, hogy az (A'B'C'D') és (ABCD) kettősviszonyok megegyeznek.
A félgömbmodell
Az inverzióval további modelleket készíthetünk. Próbálkozhatunk azzal, hogy az inverzió pólusát nem a körmodell határán, hanem azon kívül választjuk meg; ilyen módon azonban ismét a körmodellt kapjuk vissza. Ha viszont kilépünk a térbe, és az inverzió pólusát nem a körmodell síkjában választjuk meg, valóban új struktúrát kapunk. A modellt tartalmazó körlemez képe egy gömbsüveg; a pólust alkalmasan megválasztva éppen egy félgömb; az így kapott struktúra a félgömbmodell.
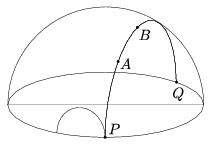
9. ábra. A félgömbmodell
A félgömbmodellben a pontok a félgömbfelület belső pontjai, az egyenesek pedig a határra merőleges félkörök. A szögek ismét az euklideszi szögek, a távolságokat pedig a (2) képlettel definiáljuk.
A félgömbmodellt könnyű közvetlenül kapcsolatba hozni a félsíkmodellel és a Cayley-Klein modellel is. Ha a félgömbmodellt az egyik határpontjából invertáljuk, a félsíkmodellt kapjuk. Ha pedig merőlegesen vetítjük a határ síkjára, a Cayley-Klein modellhez jutunk.
8. feladat. Adott egy körlemez a térben. Mi azoknak a P pontoknak a mértani helye, amikből a körlemezt invertálva félgömböt kapunk?
9. feladat. Honnan kell invertálni a félsíkmodellt, hogy a félgömbmodellt kapjuk?
10. feladat. Igazoljuk, hogy a (2) képlet a félgömbmodellben, illetve az (1) képlet a Cayley-Klein modellben ugyanazt az eredményt adja. Másképpen fogalmazva, legyen X és Y két pont a félgömbmodellben az AB félkörön, vetületük az AB egyenesre legyen X', illetve Y'. Igazoljuk, hogy (ABX'Y')= (ABXY)2.
Most már elárulhatjuk, hogyan érdemes a Cayley-Klein modellben a szögeket definiálni. Ha két egyenes hiperbolikus szögére vagyunk kiváncsiak, visszavetítjük őket a félgömbmodellre és a szöget a félgömb felületén mérjük meg. Ezt természetesen képlettel is le lehet írni (ettől most eltekintünk), de sokkal fontosabb, hogy ismerjük a képlet hátterét.
A négy bemutatott modell között összesen négy megfeleltetést találtunk; ezeket a 10. ábrán foglaltuk össze.
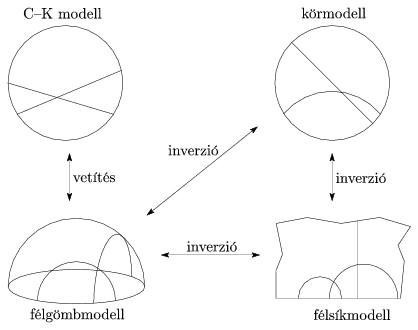
10. ábra. Megfeleltetések a modellek között
A látott modellek könnyen általánosíthatók magasabb dimenzióban. Például az irodalomban szintén jól ismert féltérmodellben [1b] egy nyílt féltér pontjai a pontok, a határsíkra merőlegesen illeszkedő félsíkok és félgömbök a hiperbolikus síkok, a határsíkra merőlegesen illeszkedő félegyenesek és félkörök az egyenesek. A hiperbolikus síkokat reprezentáló félsíkokon és félgömbökön természetesen a félsík-, illetve a félgömbmodell jelenik meg.
Csempézések
A hiperbolikus sík sokféleképpen kicsempézhető egybevágó sokszögekkel. A legegyszerűbb természetesen háromszögeket használnunk. Olyan hiperbolikus háromszöget kell választanunk, amelynek mindegyik szöge a 180o-nak egész hányada (90o,60o, 45o, 36o,...). Egyenlő szárú háromszög esetén a szárszög a 360o egész hányada (120o, 90o, 72o,...). Ha a háromszögünket lerajzoljuk valamelyik modellben, akkor az oldalakra tükrözgetve kaphatjuk meg a többi csempét.
11. feladat. Hogyan szerkeszthetjük meg a Cayley-Klein, illetve a körmodellben egy pont tükörképét egy másik pontra vagy egyenesre?
A 11. ábrán egy olyan csempézést rajzoltunk le a körmodellben, amelyben a háromszögnek egy 60 és két 45 fokos szöge van. Mivel minden csúcsban páros számú (6 vagy 8) háromszög találkozik, a csempéket ki lehet színezni két színnel úgy, hogy a szomszédos csempék különböző színűek legyenek. A kétféle színű csempébe azután kétféle mintát rajzolhatunk, mint azt Escher is tette; például az egyik fajta csempébe angyalkákat, a másik fajtába ördögöket.
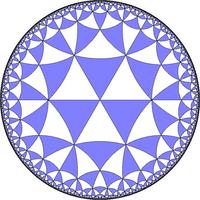
11. ábra. Csempézés a körmodellben
Hogyan rajzoljunk?
Ha számítógépes programot akarunk írni hiperbolikus grafikák készítéséhez, szükségünk van egy algoritmusra, amely a modell tetszőleges pontjának meghatározza a színét.
Vegyük fel a háromszög alakú kiinduló csempét valahol a modellben. Célszerű egyik csúcsát a modell középpontjának választani, mert így két oldala az alapkör átmérője, és az ezekre való tükrözés - amelyre szükségünk lesz - könnyebben kezelhető. A csempézésnek sokféle szimmetriája van: forgatások, tengelyes és középpontos tükrözések; ezek közül kitüntethetünk néhányat, például a modell középpontja körüli elforgatásokat, a kiinduló csempe oldalegyeneseire való tükrözéseket, esetleg - bizonyos minták esetén - oldalfelező pontokra való tükrözéseket. (Természetesen az említett transzformációk hiperbolikus megfelelőire van szükségünk; a képpontok koordinátáit számítógép segítségével érdemes meghatározni, a közölt távolságképlet felhasználásával.)
Ha P egy tetszőleges pont a modellben, amelynek színére kíváncsiak vagyunk, akkor P-t a kitüntetett transzformációkkal a kiinduló csempébe képezzük. (Ez akkor is biztosan lehetséges, ha csak a kiinduló csempe oldalaira vagy oldalfelező pontjaira való tükrözéseket használjuk.) Ha a kiinduló csempébe már belerajzoltuk a mintát, máris leolvashatjuk a P pont színét (12. ábra).
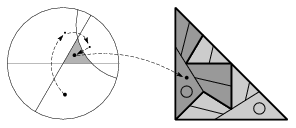
12. ábra. Pont színének meghatározása
A gyakorlatban a csempék mintáját egy külön képként rajzoljuk meg és ez a kép természetesen euklideszi.
Ezért szükségünk van még egy megfeleltetésre a csempe pontjai és az euklideszi minta között. Azt szeretnénk, hogy a csúcsok egyenrangúak legyenek és a megfeleltetés ne függjön a kiinduló csempe elhelyezésétől sem. Erre egy lehetséges megoldás a következő. Legyen a kiinduló csempe az ABC hiperbolikus háromszög, az euklideszi minta pedig az A'B'C' euklideszi háromszög. Ha P az ABC háromszöglemez egy tetszőleges pontja, akkor számítsuk ki az ABP, BCP, CAP háromszögek hiperbolikus területét. Az euklideszi mintában a P-nek megfelelő P' pontot úgy válasszuk meg, hogy az A'B'P', B'C'P', C'A'P' háromszögek területének aránya ugyanaz legyen. Más szóval, az ABP, BCP, CAP háromszögek hiperbolikus területét válasszuk a P' pont súlyponti koordinátáinak az A'B'C' háromszögben (13. ábra).
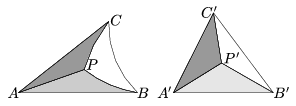
13. ábra. A területarány megőrzése
Most már minden matematikai eszköz rendelkezésünkre áll hiperbolikus grafikák készítéséhez. A program az elkészítendő kép pixelein sorban végighaladva mindegyiknek kiszámíthatja a színét és összeállíthatja a képet.
Jó szórakozást!
Kós Géza
Irodalom
[1] H. S. M. Coxeter: A geometriák alapjai (Műszaki Könyvkiadó, 1987). a) 6. fejezet (inverzió), b) 14-15. fejezet (hiperbolikus geometria).
[2] H. S. M. Coxeter - S. L. Greitzer: Az újra felfedezett geometria (Gondolat, 1977), 5. fejezet (inverzív geometria).
[3] Hajós György: Bevezetés a geometriába (Tankönyvkiadó, 1971), a) 39. fejezet (inverzió), b) 44. fejezet (projektív sík, kettősviszony), c) 46. fejezet (polaritás).
[4] Hraskó András: Pontok és nézőpontok - megjegyzések egy Kürschák feladathoz, KöMaL 2001/3, 140-146.
[5] Kiss György: A körre vonatkozó polaritás, KöMaL 1998/8, 450-455
[6] Reiman István: Geometria és határterületei (Szalay Könyvkiadó és kereskedőház Kft., 1999), a) 12. fejezet (komplex számok, inverzió, kettősviszony), b) 17. fejezet (projektív geometria és transzformációk), c) 19. fejezet (hiperbolikus sík, Cayley-Klein modell).
[7] Surányi László: Bolyai János forradalma
[8] Szilassi Lajos: Euklídész, Bolyai és a tér



