Újabb ismereteink a szabályos toroidokról
Közel negyed százada jelent meg a KöMaL-ban egy cikk a szabályos toroidokról [4]. Ezt fogjuk most kiegészíteni a témához kapcsolódó néhány friss eredménnyel. Ezek megszületését az tette lehetővé, hogy azok a számítógéppel végezhető ,,kísérletek'', amelyek annak idején hónapokat vettek igénybe, manapság másodpercek alatt elvégezhetők. Így felvethetővé - és megválaszolhatóvá - váltak olyan kérdések, amelyekre akkor gondolni sem volt érdemes. Felvetünk néhány még nem megoldott problémát is. Olyanokat, amelyek megválaszolása ma már egyáltalán nem tűnik reménytelennek.
Az itt bemutatott poliéderek ábráit az Euler3d dinamikus térgeometriai programmal tehetjük mozgathatóvá (www.euler3d.hu). Ezt ki is próbálhatják olvasóink: a cikkben az ábrákhoz tartozó linkek egy-egy Euler3d fájlra hivatkoznak. Ezeket nem csak a látvány kedvéért célszerű megnézni számítógépen, hanem azért is, mert a programról leolvashatók (kinyomtathatók) e poliéderek adatai, így ezeket az adatokat ez a cikk nem tartalmazza. Ráadásul - mint látni fogjuk - a szóban forgó eredmények épp ennek a programnak köszönhetően születhettek meg.
A szabályos toroidok három osztálya
Kezdjük egy rövid ismétléssel. Egy poliéder kombinatorikus szerkezetét tekintve szabályos, ha minden lapja ugyanannyi oldalú sokszög, és minden csúcsa ugyanannyi élhez illeszkedik. Így az a kérdés, hogy szerkezetüket tekintve milyen szabályos poliéderek léteznek, tulajdonképpen gráfelméleti, topológiai kérdés. Szabályos térképnek nevezünk egy adott felületre rajzolt gráfot, amelyben minden tartománynak p éle van és minden csúcsba q él fut be. Jelöljük ezt {p,q}-val. (Ez az ún. Schläfli szimbólum.) Közismert, hogy a gömbre rajzolt szabályos térképek: {3,3}, {3,4}, {4,3}, {3,5} és {5,3}. Ezek mindegyike realizálható egy-egy olyan poliéder formájában, amelyek élszögei és lapszögei egyenlők. Ezek a szabályos poliéderek.
A tóruszt topológiai szempontból olyan ,,nyújtható'' téglalapnak tekinthetjük, amelynek a szemközti éleit összeragasztottuk. A sík három szabályos sokszöggel, a háromszöggel, a négyzettel és a hatszöggel parkettázható ki. A mi szempontunkból ez úgy fogalmazható, hogy a síkon {3,6}, {4,4} és {6,3} alakú, tetszőlegesen sok tartományból, illetve csúcsból álló szabályos térkép létezik.
Vágjunk most ki egy ilyen szabályos térképből egy elegendően nagy téglalapot; olyat, amelyre teljesül, hogy az élei nem illeszkednek a szabályos térkép egy csúcsára sem, továbbá a szemközti téglalap-oldalakat a térképnek ugyanannyi éle metszi. Ragasszuk össze a téglalap szemközti éleit úgy, hogy a térképnek a téglalapot metsző élei is rendre csatlakozzanak a nekik megfelelő szemközti térkép-élhez. Ezzel rajzoltunk a tóruszra egy szabályos térképet. Ha ennek a tóruszra rajzolt térképnek elég sok csúcsa van, akkor nem okoz gondot a neki megfelelő poliéder előállítása sem.
Ezzel a konstrukcióval a topológiailag szabályos, tórusz-szerű poliédereknek - szabályos toroidoknak - három osztályát adtuk meg. Mindegyik osztálynak elő tudjuk állítani azokat a poliédereit, ahol a csúcsok, illetve a {6,3} osztályban a lapok száma olyan szorzat, amelynek mindkét tényezője legalább három.
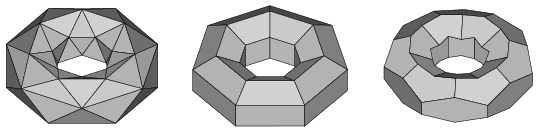
A {3,6}, {4,4}, {6,3} toroid osztály egy-egy poliédere rendre:
C= 42, L= 84, C= 42, L=42, C= 84, L= 42
Euler3d fájl Euler3d fájl Euler3d fájl
Most és a továbbiakban a poliéder fogalmát, így a toroid fogalmát is abban a szigorúbb értelemben használjuk, miszerint csak azt a geometriai alakzatot tekintjük poliédernek, amelynek lapjai egyszerű (önátmetszés nélküli, egyetlen zárt töröttvonallal határolt) sokszögek, az egy csúcsba befutó lapok egyetlen ciklust alkotnak, ahol a ciklus szomszédos elemei szomszédos, azaz közös éllel rendelkező lapok. Ebből következően a poliéder minden élére pontosan két lap és pontosan két csúcs illeszkedik. Követeljük meg azt is, hogy maga a poliéder felület se legyen önátmetsző, azaz egy lap belső pontja nem illeszkedhet a poliéder valamely másik lapjára. (Ha a poliéder fogalmát ennél általánosabban értelmezzük, akkor ezek az ún. közönséges poliéderek.)
A kérdés az, hogy a toroidok e három osztályának melyek azok a képviselői, amelyeknek a legkevesebb lapjuk, illetve csúcsuk van, továbbá vannak-e olyan szabályos toroidok, ahol a lapok, illetve csúcsok száma nem bontható fel két, 3-nál nagyobb számnak a szorzatára.
A Császár-poliéder négy változata
A kérdés első felére [1]-ben megkaptuk a választ. Császár Ákos 1949-ben igazolta, hogy a tóruszra rajzolt 7 csúcsú teljes gráf realizálható poliéderként. Ez azt jelenti, hogy létezik olyan 7 csúcsú toroid, amelynek bármely két csúcsát él köti össze, azaz nincs átlója. Itt arról is volt szó, hogy a Császár-poliédernek létezik egy szerkezetét tekintve azonos, de a csúcsok elrendezését figyelembe véve ettől ránézésre különböző változata. Két, azonos kombinatorikus szerkezetű poliédert akkor tekintünk ránézésre különbözőnek, ha az egyik nem vihető át a másikba folytonos deformálással anélkül, hogy eközben ne legyen a felület önátmetsző. Nem sokkal később két német matematikus igazolta [2], hogy a Császár-poliédernek pontosan négy, ránézésre különböző változata van.
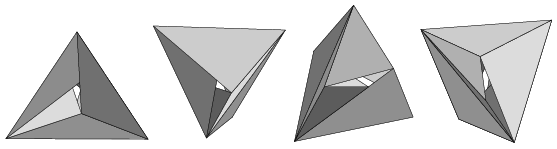
A Császár-poliéder négy, ránézésre különböző változata
Ahhoz, hogy ezt a hét csúcsú poliédert megadhassuk, először ismernünk kell a kombinatorikus szerkezetét, vagyis azt, hogy a hét pont által meghatározott \(\displaystyle {\binom{7}{3}=35}\) háromszöglap közül melyek alkotják a poliéder felületét. Ehhez számozzuk meg a háromszögrács csúcspontjait hét számmal úgy, hogy szomszédos rácspontok különböző számokat kapjanak. Egy ilyen számozási lehetőség, hogy az egy sorban levő szomszédos csúcsok folyamatosan legyenek számozva. Ezután válasszuk ki azt a téglalapot, - illetve a jelen esetben parallelogrammát, - amely a hét szám mindegyikét pontosan egyszer tartalmazza, majd ,,ragasszuk össze'' a szemközti éleit. Ez a rajzunkon azt jelenti, mintha ilyen ,,mintás'' paralelogrammák eltolással kapott példányaival parkettáznánk ki a síkot. Ezzel előállítottuk a tóruszfelületre rajzolt 7 csúcsból és 14 tartományból álló térképet. A rajzról olvasható le, hogy melyik az a 14 háromszögtartomány, amely a tóruszra rajzolt térkép tartományait alkotja. Ezek a háromszögek egyben a 7 lapú poliéder lapjai is. (A lapokat a csúcsok sorszámaival adhatjuk meg.)
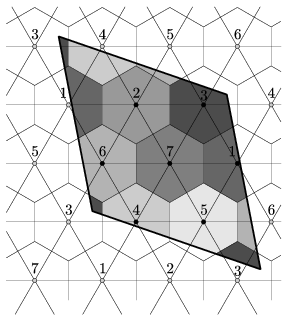
A tóruszra rajzolt teljes gráf és duálisa
fig03.txt
Eljárásunkból az is érezhető, hogy a tóruszra rajzolt bármely hét csúcsú szabályos térkép ezzel izomorf: ez a térkép bármelyikből megkapható a csúcsok átszámozásával.
E térkép alapján már ,,csak'' meg kellett adni a hét pont koordinátáit úgy, hogy az általuk meghatározott 14 háromszög közönséges, önátmetszéstől mentes poliéderfelületet alkosson.
A fenti rajz egyúttal bemutatja a térkép duálisát is, az ún. Heawood-féle hétszínű térképet, amely azt igazolja, hogy a tóruszra rajzolt térképek kiszínezéséhez szükséges legalább hét szín - ugyanis e hét tartomány mindegyike szomszédos az összes többivel [4].
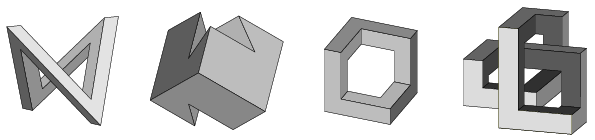
A poliéderek közötti duális kapcsolat, a Császár-poliéder duálisa
A Császár-poliéder duálisaként vált ismertté az a hét darab egyszerű hatszögből álló poliéder, amelynek bármely két lapja szomszédos.
E sorok írója - eléggé el nem ítélhető módon - [4]-ben említést sem tett arról, hogy miként lehetett rájönni egy ilyen eredményre. Itt az ideje, hogy pótoljuk ezt a hiányosságot. Annál is inkább, mert az Euler3d program lehetővé teszi, hogy bárki könnyen megismételje a tulajdonképpen már 1977-ben végzett számításokat.
A poliéderek közötti duális kapcsolat részben topológiai jellegű: egy poliéder kombinatorikus szerkezetéből egyértelműen meghatározható a duális poliéder kombinatorikus szerkezete, amelyben minden lapnak csúcs, élnek él és csúcsnak lap felel meg. A poliéderek közötti duális kapcsolatnak azonban vannak metrikus vonatkozásai is. Az eredeti poliéder szerkezetét és csúcsainak a koordinátáit ismerve elő tudjuk állítani a duális alakzat kombinatorikus szerkezetét és csúcsainak a koordinátáit is.
Legyen adott a térben egy O középpontú, r sugarú G gömb, továbbá egy O-tól különböző P pont. A P ponthoz rendeljük hozzá azt a síkot, amely merőleges az [OP) félegyenesre, és az O ponttól \(\displaystyle \frac{r^2}{OP}\) távolságra van. Ezt a síkot nevezzük a P pont G gömbre vonatkozó polársíkjának.
Hasonló módon a sík minden O-ra nem illeszkedő síkjához is hozzárendelhető egy pont, amelyet a sík G-re vonatkozó pólusának fogunk nevezni. Legyen T az O pontnak az adott síkra eső merőleges vetülete. A sík pólusa essen az [OT) félegyenesre, és az O-tól mért távolsága legyen \(\displaystyle \frac{r^2}{OT}\).
Ezt a - pontnak síkot, síknak pontot megfeleltető - hozzárendelést a G gömbre vonatkozó polaritásnak nevezzük.
A fenti definíciókból kitűnik, hogy miért zártuk ki a polaritás értelmezési tartományából az O pontot, valamint az O-ra illeszkedő síkokat. (Megvan egyébként a lehetőség arra, hogy kibővítsük az euklideszi teret a végtelen távolinak, vagy ideálisnak nevezett pontok, egyenesek és sík fogalmával, ekkor már értelmezhető a polaritás az O pontra illeszkedő síkokra, egyenesekre, sőt magára az O pontra is. Ezzel a projektív geometria foglalkozik.)
Nyilvánvaló, hogy ha például az A pontnak a G gömbre vonatkozó polársíkja \(\displaystyle \alpha\), akkor az \(\displaystyle \alpha\) síknak ugyanerre a gömbre vonatkozó pólusa A, vagyis a gömbre vonatkozó polaritás négyzete a mindent helyben hagyó identikus transzformáció.
Be fogjuk látni, hogy ha egy pont végigfut a tér valamely O-t nem tartalmazó e egyenesén, akkor a polársíkjai ugyancsak egy egyenesre illeszkednek. Ezt nevezzük az adott egyenes poláris egyenesének, röviden polárisának.
Rajzoljuk le ennek a térgeometriai helyzetnek az (O,e) síkba eső ,,síkmetszetét''. Legyen T az O pont e-re eső merőleges vetülete, p' a P\(\displaystyle \in\)e pont polársíkjának az (O,e) síkkal alkotott metszésvonala, ennek az [O,T) félegyenessel alkotott metszéspontja T'. Ekkor \(\displaystyle POT\triangle\approx T'OP'\triangle\), mivel mindkettő derékszögű háromszög, és egyik hegyesszögük közös. Ebből \(\displaystyle {\frac{OP}{OT}=\frac{OT'}{OP'}}\), azaz OT.OT'= OP.OP'. A P pont polársíkjának a G gömb O középpontjától mért távolsága \(\displaystyle OP'= \frac{r^2}{OP}\). Ezért az is teljesül, hogy a T' pontra illeszkedik a T pontnak, sőt az e egyenes minden pontjának a polársíkja. E síkok mindegyike merőleges az (O,e) síkra, így közös metszésvonaluk a T' pontra illeszkedő e-re merőleges e' egyenes lesz. Ez az e egyenes G-re vonatkozó poláris egyenese. Pontosan ugyanígy látható be, hogy ha egy pont illeszkedik az e' egyenesre, akkor polársíkja illeszkedik e-re.
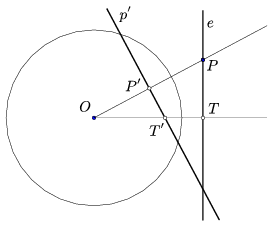
A polaritás illeszkedéstartó tulajdonsága
fig04.txt
Ezzel azt is beláttuk, hogy az így értelmezett gömbre vonatkozó polaritás illeszkedéstartó: ha két pont illeszkedik egy egyenesre, akkor ezek polársíkjai illeszkednek az egyenes poláris egyenesére, ha egy pont illeszkedik egy síkra, akkor a pont polársíkja illeszkedik a sík pólusára.
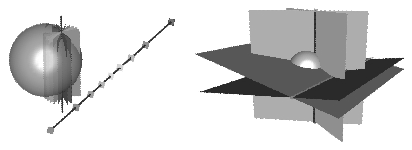
A gömbre vonatkozó polaritás illeszkedéstartó
Adjunk meg a térben derékszögű koordinátáival egy, az origótól különböző P(a,b,c) pontot. Be lehet látni, hogy a P pontnak az origó középpontú r sugarú gömbre vonatkozó polársíkja az a.x+b.y+c.z=r2 egyenletű sík lesz. Eszerint, ha koordinátageometriai eszközökkel dolgozunk (mint azt az Euler3d teszi), könnyen megadható egy sík három, nem egy egyenesre eső pontja polársíkjának az egyenlete, és a kapott három elsőfokú egyenletből álló egyenletrendszer megoldásaként magának a síknak a pólusa.
Ahhoz azonban, hogy ezt a transzformációt poliéderek csúcsaira, lapjaira, éleire alkalmazhassuk, értelmeznünk kell, hogy mit értsünk egy poliéder élének (mint szakasznak) a poláris alakzatán.
Legyen P egy közönséges poliéder, legyen továbbá G egy olyan gömb, amelynek a középpontja a P poliéder egyetlen lapjának a síkjára sem illeszkedik.
Mivel a közönséges poliédereknek bármely élére pontosan két lap, és pontosan két csúcs illeszkedik, az egy élre illeszkedő két lap síkjának a G gömbre vonatkozó pólusaként kapott két pont illeszkedik a kiválasztott él egyenesének a poláris egyenesére. Így e két pont meghatároz egy olyan szakaszt, amely merőleges az adott élre. Ezt a szakaszt nevezzük az adott él polárisának.
Egy közönséges poliéder minden csúcsára véges sok él illeszkedik, amelyek egy adott ciklikus sorrendben meghatározzák a poliéder egy testszögletét. Ugyanez a ciklikus sorrend meghatározza, hogy az egy csúcsra illeszkedő élek polárisai (mint szakaszok) milyen sorrendben kapcsolódnak egymáshoz. Így a P poliéder testszögletének a G-re vonatkozó poláris alakzata egy zárt síkbeli sokszögvonal lesz. Ezt nevezzük a testszöglet polárisának.
Ugyanígy egy zárt sokszögvonalnak a G gömbre vonatkozó poláris alakzata egymáshoz közös szögszárban csatlakozó szögekből álló alakzat lesz.
Ha egy poliéder valamely testszöglete konvex, és a G gömb középpontja a testszöglet belsejében van, akkor a testszögletet meghatározó élek G-re vonatkozó poláris alakzatai konvex sokszöget határoznak meg.
Ha egy poliéder konvex, és a polaritás alapgömbjének a középpontja a poliéder belső pontja, akkor összes testszögletének a G-re vonatkozó poláris alakzatai (mint konvex síkbeli sokszögek) egy ugyancsak konvex poliédert határoznak meg. Ezt nevezzük a P poliéder G-re vonatkozó duális poliéderének. Természetesen erre is teljesül, hogy minden élére pontosan két csúcs és pontosan két lap illeszkedik. Emiatt a duális poliéderhez is tartozik egy kombinatorikus szerkezet, amely ugyancsak a lapok listájával írható le egyértelműen.
Ha egy poliéder nem konvex (esetleg nem is egyszerű poliéder), vagy a duális alakzat képzéséhez használt gömb nincs ugyan a poliéder belsejében, de középpontja nem illeszkedik egyik lapjának a síkjára sem, akkor előfordulhat, hogy egy testszöglet duális alakzata önátmetsző sokszögvonal lesz, vagy maga a keletkező testszöglet válik önátmetszővé. Azonban ekkor is teljesül, hogy ebből - a poliédernek csak a legáltalánosabb értelemben nevezhető térgeometriai alakzatból - visszanyerhető az eredeti poliéder, ha ugyanarra a gömbre nézve képezzük a duális alakzatát.
Ezekre az összefüggésekre gondolva jutottunk (1976-ban) arra az ötletre, hogy képezzük a Császár-poliédernek egy adott gömbre vonatkozó duálisát. A Császár-poliédernek az a tulajdonsága, hogy bármely két csúcsát él köti össze, a duális alakzatnak azt a tulajdonságát adja, hogy bármely két lapnak van közös éle.
A dolog azonban korántsem megy ilyen simán. Ugyanis a Császár-poliéder szükségképpen konkáv, így semmi nem biztosítja, hogy a duális alakzat egy-egy lapja ne legyen önátmetsző sokszög. Önátmetsző lapjai pedig nem lehetnek a keresett poliédernek. Az is előfordulhat, hogy bár a kapott alakzat minden lapja egyszerű sokszög, maga a poliéder felület azonban önátmetsző: egy-egy lap belső pontja egyben pontja egy másik lapnak is.
Ezeknek a nem kívánatos eseteknek a kiküszöbölésére különböző ,,szűrőket'' kellett készíteni. Pl. a programozásban jártas olvasóink gondolják végig, hogy miként tudnák rábírni a számítógépet annak a kérdésnek a megválaszolására, hogy ha adott egy egyszerű, de esetleg konkáv hatszög, továbbá egy hetedik pont, akkor ez a pont vajon belül van-e a sokszögön, vagy nem. (A '70-es években még nagyon lassú és manapság már elképzelhetetlenül kicsi memóriával rendelkezett ,,a'' számítógép, amely ,,természetesen'' rajzolni sem tudott.)
Néhány hónapos kísérletezés eredményeképpen így is sikerült megtalálni a szóban forgó poliédert. Ez a kísérletezés lényegében abból állt, hogy a Császár-poliéder kombinatorikus szerkezetét változatlanul hagyva addig kellett változtatgatni a csúcsok koordinátáit (nem törődve azzal, hogy az eredeti poliéder felület esetleg önátmetszőnek bizonyul), amíg a duális alakzat nem vált a keresett közönséges poliéderré. Ez a ,,lövés a sötétbe'' módszer azonban - jobb híján - ma is alkalmazható, sokkal hatékonyabb technikai körülmények között.
Az első modell ismeretében már könnyű volt finomítani az adatokon, sőt elemi bizonyítást adni a poliéder létezésére. Az is könnyen belátható, hogy 7-nél kevesebb lapja nem lehet egy {6,3} típusú szabályos toroidnak.
Néhány további, hatszöglapú szabályos toroid
Felvethető a kérdés, hogy vajon mely n értékre létezik n-lapú közönséges poliéder a szabályos toroidok három osztályában.
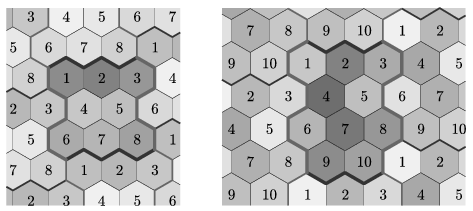
A négyszögekből és 4 fokszámú csúcsokból álló {4,4} osztályban könnyen előállíthatók olyan toroidok, ahol n=pq, ahol p és q legalább 3. Tudunk rajzolni a tóruszra például 10, vagy 11 tartományú (és csúcsú) térképet, azonban ilyen 10 vagy 11 lapú toroid valószínűleg nem létezik. (A konstruktív geometriában sokkal nehezebb az ,,ilyen nincs'' típusú állításokat igazolni, mint az ellenkezőjét.)
A {3,6} típusú, háromszögekből álló szabályos toroidok közül legkevesebb csúcsa a Császár-poliédernek van. Az írásunkhoz tartozó weblapon bemutatjuk az osztály 8, 9 és 10 csúcsú poliéderét is. Úgy tűnik, nem túl nehéz feladat ilyen poliédert találni bármely, ezeknél nagyobb csúcs-szám esetén sem.
A legérdekesebb kérdés a hatszögekből álló {6,3} típusú szabályos poliéderek körében vethető fel. Konstruktív úton igazolható, hogy létezik n hatszögből álló szabályos toroid, ha n=pq, ahol p\(\displaystyle \ge\)3 és q\(\displaystyle \ge\)3.
Példaként bemutatunk egy n=9 hatszögből álló toroidot, amelyet úgy kaptunk, hogy egy három élű prizmát kivágtunk egy kockából. A prizma három éle párhuzamos a kocka testátlójával. Ugyancsak könnyen konstruálható 12 vagy 15 hatszögből álló szabályos toroid is.
Áthidaló 8 lapú, valamint 9, 12 és 24 lapú szabályos toroidok
Euler3d fájl Euler3d fájl Euler3d fájl Euler3d fájl
A 12 L-alakú hatszögből álló toroid két irányban is ötletet adhat. Az itt látható 24 L-alakú lapból álló toroid ugyanebbe az osztályba tartozik, noha az általa előállított tórusz lényegében egy ,,csomó''. Maga a poliéder-felület homeomorf (azaz topológiai szempontból azonos) a mentőöv-szerű tórusszal.
A 12 L-alak adhatott ötletet J. Schwörbelnek, aki elsőként állított elő egy n=8 lapból álló szabályos toroidot [3]. Ennek azonban van egy kellemetlen tulajdonsága. Ez egy ún. áthidaló poliéder: vannak olyan lapjai, amelyek két él mentén is szomszédosak. Vajon van-e olyan 8 hatszögből álló toroid, amelynek nincs áthidaló lap-párja? Ugyanilyen kemény dió annak az eldöntése, hogy van-e n = 10, 11, 13 vagy 14 lapú {6,3} típusú toroid.
E kérdések eldöntésére úgy tűnik nincs jobb lehetőség, mint a hétlapú toroidnál látott próbálkozás módszere, amely azonban éppen az Euler3d program felhasználásával nem feltétlenül reménytelen.
Első lépésként meg kell határoznunk a keresett n-lapú poliédernek, illetve duálisának a kombinatorikus szerkezetét. Ehhez vegyünk a síkon egy szabályos hatszögrácsot. Számozzuk meg a lapjait az 1...n számokkal úgy, hogy az azonos sorszámú lapok szomszédai minden esetben azonos sorrendben ugyanolyan sorszámú lapok legyenek. Ez elérhető például úgy, hogy a hatszögrács minden sorát ciklikusan megszámozzuk az 1...n számokkal, a sorokat egymáshoz képest úgy eltolva, hogy a kívánt feltétel teljesüljön. Példaként bemutatjuk a 8 és 10 hatszöghöz tartozó számozást. Ebből ,,kivágható'' - akár többféleképpen is - az az n hatszög, amely a tóruszra rajzolt {6,3} típusú térképet adja. (Az egymástól eltérő kivágások és azok tórusszá ragasztása izomorf térképeket eredményez). Az így kapott térkép duálisán ugyanezek a sorszámok a háromszögrács csúcsait jelentik.
A tóruszra rajzolt 8, illetve 10 lapú szabályos térkép
Miután megkaptuk a {3,6} típusú n csúcsú toroid kombinatorikus szerkezetét, vegyünk fel hozzá koordinátákat lehetőleg minél ,,szellősebben'', majd próbáljuk úgy megválasztani a koordinátákat, hogy a poliéder duálisa a keresett toroid legyen, amelynek minden lapja egyszerű hatszög. (Itt jegyezzük meg, hogy ez a rövid bekezdés olykor hosszas, esetleg eredménytelen kísérletezést jelent.)
Itt bemutatjuk az ilyen úton kapott 8, 10 és 11 lapú szabályos toroidot. Az e cikket tartalmazó weblapon megmutatjuk azt a hosszadalmas kísérletezést is, amely ezekhez az eredményekhez vezetett. Egyelőre nyitott kérdés, hogy vajon létezik-e 13, vagy 14 lapú szabályos toroid a {6,3} osztályban. Ahogy növekszik a lapok száma, egyre reménytelibbnek tűnnek az itt vázolt kísérletek. Bár ez koránt sem biztos. Ugyanis minden feladat nehéz, amíg nem ismerjük a megoldását, és könnyű, ha már ismerjük.
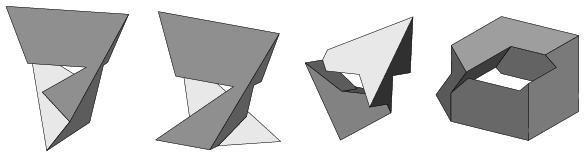
7, 8, 10 és 11 lapú szabályos toroidok
és az ezzel kapcsolatos kísérletek: 7 lap; 8
lap; 10 lap és 11 lap
Ha már találtunk egy megfelelő megoldást, akkor a koordináták ,,finom'' változtatásával elérhető, hogy a kapott poliédernek legyenek egybevágó lapjai, rendelkezzen valamilyen - például tengelyes - szimmetriával, egész számok legyenek a koordinátái stb. Ezek azonban már csak apróbb csiszolások.
Ugyancsak apróbb csiszolásnak tekinthető, hogy egy már meglévő modell ismeretében tudunk elemi, ,,szalonképes'', a vaktában lövöldözést mellőző bizonyítást is adni a poliéder létezésére.
Ha azonban ez a ,,szép'' bizonyítás úgy kerül elénk, mint a nyúl a bűvész kalapjából, akkor éppen arra az útra nem derülne fény, amely ezekhez az eredményekhez vezetett.
Szilassi Lajos
Irodalom
[1] Bokowski, J. - Eggert, A.: All realizations of Möbius' torus with 7 vertices, Structural Topology (1991), 17: 59-78.
[2] Császár, Á.: A polyhedron without diagonals, Acta Sci. Math. Universitatis Szegediensis, 13 (1949-50), pp. 140-142.
[3] J. Schwörbel, Die kombinatorisch regulären Tori, Dipl. thesis, Siegen University (1988).
[4] Szilassi L.: Szabályos toroidok, KöMaL (1983), 8-9. sz., 97-104.
