Miért természetes az $e$?

Amikor az exponenciális függvény és a logaritmus fogalmát tanuljuk, a $2$-es és a $10$-es alap választása tűnik a legkézenfekvőbbnek. A $2$-es alap előnye, hogy a kis pozitív egész számok között sok olyan van, aminek a $2$-es alapú logaritmusa egész. A $10$-es alap előnye pedig az, hogy sokjegyű számok logaritmusát is nagyon könnyű egyetlen, néhány oldalas logaritmustábla segítségével meghatározni. Amilyen természetesnek tűnik a $2$-es és a $10$-es alapú logaritmus, olyan megdöbbentő, hogy "természetesnek" mégsem ezeket nevezzük, hanem egy teljesen mesterséges számot választunk alapul. Ezt a mesterséges alapot Euler nyomán $e$-vel jelöljük, értéke közelítőleg \(\displaystyle e \approx\)2,71828182845904523536.

Az $e$ számot a legtöbb tankönyv az \(\displaystyle \left(1+\frac{1}{n}\right)^{n}\) sorozat határértékeként, tehát egy \(\displaystyle 1^\infty\) alakú határértékként definiálja. Mások (Eulerhez hasonlóan) így definiálják: \(\displaystyle e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\cdots.\) Egyik definíció sem alkalmas arra, hogy az $e$-vel közvetlenül aritmetikai műveleteket végezzünk. Sőt, Euler, Liouville és Hermite eredményeiből azt is tudjuk, hogy az $e$ szám semmilyen egész együtthatós polinomnak sem gyöke; más szóval, a $\pi$-hez hasonlóan, transzcendens [3]. Az $e$ számmal nem könnyű számolni.

Különösen a komplex függvénytan mutatott rá, hogy az $e^x$ függvény nagyon szoros kapcsolatban áll a trigonometrikus függvényekkel, és ezáltal az $e$ közeli rokona a $\pi$-nek. Nagyon sok olyan eset van, amikor ez a két szám együtt fordul elő egy matematikai eredményben, például a Stirling-formula szerint \(\displaystyle n!\sim\sqrt{2\pi n}\left(\frac{n}{e}\right)^{n}\).

Az $e$ szám tehát nem azért természetes, mert könnyű vele számolni, hanem mert olyan speciális tulajdonságai vannak, amelyek matematikai vizsgálatokban sokkal fontosabbak, mint az aritmetikai kezelhetőség. Ebben a cikkben az egyik — a legfontosabb — tulajdonságát fogjuk vizsgálni, amely ott áll az összes többi hátterében.

Egy kis matematikatörténet

A XV–XVI. század Európájában egyre fontosabbá vált az ipar, a hajózás, a csillagászat, a kereskedelem, mely területek nemcsak műszaki, hanem matematikai vívmányoknak is köszönhették azt, hogy egyre professzionálisabbá váltak. A pénzemberek számára oly fontos kamatos kamat számításához táblázatokat készítettek (pl. Simon Stevin). Az ezekkel való számolást szerette volna Joost Bürgi (1552–1632) felgyorsítani az általa készített táblázat segítségével. A svájci műszerkészítő mester adott $p$ kamatláb mellett az \(\displaystyle \left(1+\frac{p}{100}\right)^{n}\), ($n=0,1,2,\ldots$) mértani sorozathoz elemenként a $0, 10, 20, \ldots, 10n$ számtani sorozat elemeit rendelte. Így az első sorozat bármely két elemének szorzatához éppen az a szám tartozik, amely a megfelelő számtani sorozatból való elemek összege. A két sorozatot egymástól színezéssel különböztette meg (piros-fekete). A ma már természetes jelöléssel tehát \(\displaystyle \log_{a} \left(1+\frac{p}{100}\right)^{n}=10n\).

A táblázat ugyan már 1611-ben elkészült, ám csak kilenc évvel később jelent meg. Ennek köszönhette John Napier skót matematikus, hogy először az övé vált ismertté (1614). Napier munkája annak a mozgásnak a közelítő leírásából származik, amikor valaki egy $d$ hosszúságú úton halad úgy, hogy sebességének mérőszáma minden pillanatban megegyezik a hátralevő út hosszával. Az időt rövid, $\lambda$ hosszúságú szeletekre vágta, és a sebességet minden szeletben állandónak vette. Az így kapott út-idő értékekből táblázatot készített. A megfeleltetést a görög logosz, azaz arány és arithmosz, azaz szám összegyúrásából latinosan logaritmusnak nevezte el.

A táblázat elkészítésekor Napier a $\lambda$ számot $10^{-7}$-nek választotta ($d$-t pedig $10^7$-nek), mai szóhasználattal tehát azt is mondhatjuk, hogy Napier-féle táblázatban a logaritmus alapja \(\displaystyle \left(1-\frac{1}{10^7}\right)^{10^7}\).

Napier munkáját az Oxfordi Egyetem geometria professzora, Henry Briggs fejlesztette tovább. Elsőként azt szerette volna, hogy $\log 1=0$, azaz az alapszakasz hossza $10^7$ helyett egységnyi legyen. Másodsorban kívánatosnak tartotta, hogy a $10$ logaritmusa tíznek egy hatványaként álljon elő. Számos lehetőség megvitatása után a $\log 10=1$ mellett döntöttek, ami nemcsak a tízes alapú logaritmus megszületését jelentette, hanem magának a logaritmus alapjának megfogalmazását is. (Tehát ha egy szám $a$-nak az $L$-edik hatványa, akkor a szám $a$ alapú logaritmusa $L$.)

A 2,718... szám első ismert előfordulását Napier Descriptio című műve angol fordításának függelékében találhatjuk. (A függeléket feltehetőleg William Oughtred írta.) Itt szerepel a következő megállapítás: log_a 10=2,302585, ahol a\(\displaystyle \approx\)2,71828. Egy másik érdekes korai eredmény Gregory of Saint-Vincent nevéhez fűződik, aki 1647-ben a derékszögű hiperbola alatti területet számította ki. Szerinte az xy=1 egyenletű hiperbola és az $x$-tengely egységnyi területet fog közre az x=1-től kezdve x=e-ig.

Euler az $e$ számot az 1727–28-ból származó Elmélkedés az ágyúzás legújabb tapasztalatairól (Meditatio en experimenta explosione tormentorum nuper instituta) című kéziratában használta először. Később egy — Goldbachnak írt — levelében találkozhatunk az $e$-vel (1731), nyomtatásban legelőször 1736-ban jelent meg a Mechanica című tanulmányban.

A szimbólum megválasztásának miértjéről csak találgatni lehet. Vannak, akik szerint az $e$ az exponenciális szó kezdőbetűje, mások az a, b, c, d — az akkori matematikát művelők között bevetten használt — betűk sorában következőt látják benne. A rosszmájúak és irigyek véleménye természetesen az, hogy Euler a számot önmagáról nevezte el.

Euler megmutatta, hogy az $e$ szám irracionális. 1844-ben Liouville bebizonyította, hogy egyetlen egész együtthatós másodfokú polinomnak sem gyöke, sőt, Hermite 1873-ban azt is bebizonyította, hogy transzcendens.

A komputertechnika fejlődésével egyre több jegyét számolják ki $e$-nek, a minél pontosabb meghatározásért folyó verseny napjainkban is tart. (1999-ig 10⁹ nagyságrendű tizedes jegyet állapítottak meg.)

Az exponenciális függvény meredeksége

Az $e$ szám legérdekesebb és egyben legfontosabb tulajdonsága az exponenciális és logaritmusfüggvények meredekségével kapcsolatos.

A különféle alapú exponenciális függvények grafikonjait a középiskolából viszonylag jól ismerjük. Az x\(\displaystyle \mapsto\)a^x függvény szigorúan monoton nő, ha a>1, szigorúan monoton fogy, ha 0<a<1 és azonosan 1, ha a=1. Minden esetben igaz az, hogy a grafikon egy folytonos görbe, amely átmegy a (0;1) ponton.

Tetszőleges alap esetén igaz, hogy az a^x függvény konvex. Ez szemléletesen azt jelenti, hogy a grafikon bármelyik két pontját egy egyenes szakasszal összekötve, a szakasz a grafikon fölött helyezkedik el (1. ábra).

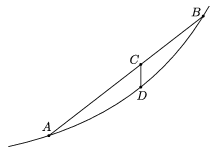
1. ábra

A konvexitást formálisan is leírjuk. Legyen A=(x;a^x) és B=(y;a^y) a két végpont. Az AB szakasz egy belső C pontját úgy határozzuk meg, hogy a szakaszt valamilyen arányban felosztjuk. Ha az arány q:p, ahol p, q pozitív számok és p+q=1, akkor az osztópont koordinátái C=(px+qy;pa^x+qa^y), a grafikon C ,,alatti'' pontja pedig D=(px+qy;a^px+qy). Az tehát, hogy az exponenciális függvény konvex, azt jelenti, hogy a^px+qy\(\displaystyle \le\)pa^x+qa^y teljesül bármelyik lehetséges $x$, y, p, q számnégyes esetén.

Azt, hogy az exponenciális függvény konvex, a súlyozott számtani és mértani közepek közötti egyenlőtlenség segítségével bizonyíthatjuk be. Az a^px+qy és pa^x+qa^y kifejezések nem mások, mint az a^x és a^y számok súlyozott mértani, illetve számtani közepe a p és q súlyokkal.

Az exponenciális függvény grafikonjához bármelyik pontjában, így a (0;1) pontban is érintőt húzhatunk. (Ennek bizonyításától most eltekintünk.) Az érintő meredeksége természetesen attól függ, hogy mi az alap. A továbbiakban arra vagyunk kiváncsiak, hogy milyen alap esetén lesz a (0;1)-ben húzott érintő meredeksége 1, azaz mikor érinti az exponenciális függvény az y=x+1 egyenest. A keresett alapot jelöljük — egyelőre — a-val.

Az a számra jó becsléseket az érintő (0;1)-hez közeli pontjai segítségével kaphatunk. Először vegyünk egy nagy pozitív valós számot ($x$) és tekintsük az \(\displaystyle \left(\frac{1}{x};1+\frac{1}{x}\right)\) pontot. A konvexitás miatt a teljes érintő a grafikon alatt van (kivéve az érintési pontot, 2. ábra), tehát \(\displaystyle a^{\frac{1}{x}} \gt 1+\frac{1}{x}\); $x$-edik hatványra emelve \(\displaystyle a \gt \left(1+\frac{1}{x}\right)^{x}\).

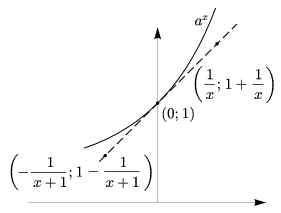
2. ábra

Második becslésünkhöz tekintsük a \(\displaystyle \left(-\frac{1}{x+1}; 1-\frac{1}{x+1}\right)\) pontot. Ez a pont is a grafikon alatt van, tehát \(\displaystyle a^{-\frac{1}{x+1}} \gt 1-\frac{1}{x+1}\). Ezúttal $-(x+1)$-edik hatványra emelve (mivel a kitevő negatív, az egyenlőtlenség iránya megfordul!),

\(\displaystyle a<\left(1-\frac{1}{x+1}\right)^{-(x+1)}= \left(1+\frac{1}{x}\right)^{x+1}. \)

Összefoglalva, a keresett alapra teljesülnie kell, hogy tetszőleges x>0 esetén

\(\displaystyle \left(1+\frac{1}{x}\right)^{x} \lt a \lt \left(1+\frac{1}{x}\right)^{x+1}. \)

Itt azonnal meg lehet kérdezni, hogy az $x$ helyére nagyobb számot írva erősebb becslést kapunk-e. Megmutatjuk, hogy így van, az \(\displaystyle x\mapsto\left(1+\frac{1}{x}\right)^{x}\) függvény monoton nő, az \(\displaystyle x\mapsto\left(1+\frac{1}{x}\right)^{x+1}\) függvény pedig monoton fogy.

Legyen 0<u<v két tetszőleges pozitív valós szám. Először azt fogjuk megmutatni, hogy \(\displaystyle \left(1+\frac{1}{u}\right)^{u} \lt \left(1+\frac{1}{v}\right)^{v}\). Legyen \(\displaystyle b=\left(1+\frac{1}{u}\right)^{u}\); az x\(\displaystyle \mapsto\)b^x függvény grafikonja átmegy az \(\displaystyle U=\left(\frac{1}{u};1+\frac{1}{u}\right)\) ponton (3. ábra).

A konvexitás miatt a \(\displaystyle V=\left(\frac{1}{v};1+\frac{1}{v}\right)\) pont a b^x függvény grafikonja fölött van, tehát \(\displaystyle 1+\frac{1}{v}\gt b^{\frac{1}{v}}\). A v-edik hatványokat véve

\(\displaystyle b=\left(1+\frac{1}{u}\right)^{u} \lt \left(1+\frac{1}{v}\right)^{v}. \)

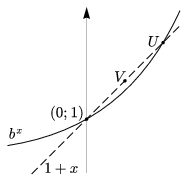
3. ábra

Legyen most \(\displaystyle c=\left(1+\frac{1}{u}\right)^{u+1}\). Az x\(\displaystyle \mapsto\)c^x függvény grafikonja átmegy a \(\displaystyle P=\left(-\frac{1}{u+1};1- \frac{1}{u+1}\right)\) ponton. A \(\displaystyle Q=\left(-\frac{1}{v+1};1- \frac{1}{v+1}\right)\) pont a grafikon fölött van, tehát \(\displaystyle c^{-\frac{1}{v+1}}<1-\frac{1}{v+1}\). Ezt -(v+1)-edik hatványra emelve az egyenlőtlenség iránya ismét megfordul, \(\displaystyle c=\left(1+\frac{1}{u}\right)^{u+1} \gt \left(1+\frac{1}{v}\right)^{v+1}\) (4. ábra).

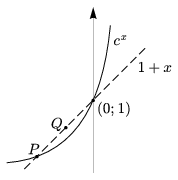
4. ábra

Természetesen mindkét függvény monotonitását közvetlenül is igazolhatjuk a súlyozott közepek közötti egyenlőtlenségekkel. Írjuk fel az \(\displaystyle 1+\frac{1}{u}\) és 1 számokra a számtani és mértani közép közötti egyenlőtlenséget az u, illetve v-u súlyokkal:

\(\displaystyle \left(\left(1+\frac{1}{u}\right)^{u}\cdot1^{v-u}\right)^{\frac{1}{v}}< \frac{u\cdot\left(1+\frac{1}{u}\right)+(v-u)\cdot1}{v},\)

\(\displaystyle \left(1+\frac{1}{u}\right)^{u}< \left(1+\frac{1}{v}\right)^{v}.\)

Hasonlóan írjuk fel a súlyozott harmonikus és mértani közepek közötti egyenlőtlenséget is az u+1 és v-u súlyokkal:

\(\displaystyle \frac{v+1}{\frac{u+1}{1+\frac{1}{u}}+\frac{v-u}{1}} \le\left(\left(1+\frac{1}{u}\right)^{u+1}\cdot1^{v-u}\right)^{\frac{1}{v+1}},\)

\(\displaystyle \left(1+\frac{1}{v}\right)^{v+1} <\left(1+\frac{1}{u}\right)^{u+1}.\)

A monoton növekvő alsó becslés és a monoton fogyó felső becslés hányadosa 1-hez tart. Ebből következik, hogy a két függvénynek közös határértéke van a végtelenben (5. ábra). Ha a közös határértéket (amit most már nyugodtan nevezhetünk $e$-nek) választjuk az exponenciális függvény alapjának, a (0;1) pontbeli érintő iránya éppen 45^o-os lesz. Az $e$ számnak ez az a tulajdonsága, ami miatt a matematika legkülönfélébb területein felbukkan.

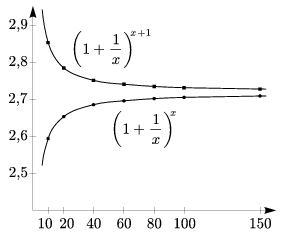
5. ábra

Az $e^x$ függvénynek nem csak a (0;1)-beli meredeksége érdekes. A grafikon tetszőleges (x;$e^x$) pontjában az érintő meredeksége éppen $e^x$, vagy más szóval, ($e^x$)'=$e^x$. Ez a tulajdonság is az előbb látottak egyszerű következménye.

A célunk az volt, hogy rámutassunk az okra, ami miatt az \(\displaystyle \left(1+\frac{1}{n}\right)^{n}\) sorozat határértéke különleges, hogy miért éppen ezt a számot érdemes az exponenciális és a logaritmusfüggvény alapjának választani.

Egy tankönyvben, ahol a gondos, precíz felépítés nagyon fontos, a sorrend többnyire teljesen más. Az $e$ számot jóval azelőtt szokás definiálni, mint hogy érintőkről és azok meredekségéről, azaz differenciálásról szó esne. Előbb — a sorozatok határértékéről szóló fejezetekben — bebizonyítjuk, hogy az \(\displaystyle \left(1+\frac{1}{n}\right)^{n}\) sorozat konvergens, és a határértékét elnevezzük $e$-nek. Csak később, a függvények határértéke és a folytonosság fogalmának bevezetése után, a differenciálásról szóló fejezetben találkozunk azzal, hogy az $e^x$ függvény milyen érdekes a deriválás szempontjából.

Feladatok

1. Legyen n tetszőleges pozitív egész. Adjunk közvetlen bizonyítást arra, hogy \(\displaystyle \left(1+\frac{1}{n}\right)^{n}<3\).

2. Bizonyítsuk be, hogy \(\displaystyle 1+\frac{1}{1!}+\frac{1}{2!}+ \frac{1}{3!}+\ldots=e\).

3. Bizonyítsuk be, hogy tetszőleges a valós szám esetén az \(\displaystyle \left(1+\frac{a}{x}\right)^{x}\) függvénynek van határértéke a \(\displaystyle \infty\)-ben.

4. Definiáljuk az \(\displaystyle \exp\) függvényt a következőképpen: \(\displaystyle \exp\,(a)=\lim_{x\to\infty}\left(1+\frac{a}{x}\right)^{x}\). Mutassuk meg, hogy \(\displaystyle \exp\,(a+b)=\exp\,(a)\cdot\exp\,(b)\), és valójában \(\displaystyle \exp\,(a)=e^a\).

5. Bizonyítsuk be, hogy \(\displaystyle e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+ \frac{x^3}{3!}+\ldots\,.\)

Hátha valaki nem ismeri

A differenciáloperátor összetalálkozik egy függvénnyel. Azt mondja neki az operátor:
- Add nekem az értékkészletedet, különben megderivállak!
- Hahaha! Én vagyok az $e^x$.

Az $e$ tizedes jegyeinek megjegyzésére több vicces mondatot, verset gondoltak ki, amelyekben minden számjegynek egy-egy szó betűinek száma felel meg, például

,,By omnibus I traveled to Brooklyn.''

,,We present a mnemonic to memorize a constant so exciting that Euler exclaimed: `!' when first it was found, yes, loudly `!'. My students perhaps will compute $e$, use power or Taylor series, an easy summation formula, obvious, clear, elegant!'' (Barel, 1995)

Irodalom

[1] Eli Maor: $e$ — The history of a number, Princeton University Press (Princeton, New Jersey, 1994).

[2] Sain Márton: Nincs királyi út, Gondolat (Budapest, 1986).

[3] Freud Róbert – Gyarmati Edit: Számelmélet, Nemzeti Tankönyvkiadó (Budapest, 2000), 369-401. oldal.

[4] http://mathworld.wolfram.com/e.html

[5] http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/e.html

Kós Rita – Kós Géza