Lajos Lóczi:

On commutative and associative powers

Addition and multiplication both obey the law of commutativity

a+b=b+a and a^.b=b^.a,

and associativity

(a+b)+c=a+(b+c) and (a^.b)^.c=a^.(b^.c),

for any real numbers a,b and c. However, powers fail to be commutative and associative, as we know in general

a^b $ne$ b^a and a^{(b^c)} $ne$ (a^b)^c.

In spite of this, equality may hold in special cases. Our aim is to determine all positive real pairs (x,y) and triples (x,y,z) satisfying

(1)

x^y=y^x

and

(2)	x^{(y^z)}=(x^y)^z,

respectively, then, with their help study the integer and rational solutions as well.

1 The commutative case

First, we want to find the positive real solutions of (1). (The reason we confine our attention to the positive case only is that powers in general are not defined for negative bases in the set of real numbers, furthermore, the case when one of the variables is equal to zero does not seem too compelling either.) To start with, let us try to guess some solutions. We soon find x=2 and y=4 (or vice versa, because of the symmetry). Since (1) does not seem to admit any other positive integer solutions, let us try some radicals. If we are lucky, we discover 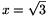$x=\sqrt{3}$ and $\displaystyle y=3\sqrt{3}$, since

$\displaystyle (3\sqrt{3})^{\sqrt{3}}=(\sqrt{3}^{\,3})^{\sqrt{3}}={\sqrt{3}}^{\,3\sqrt{3}}.$

The point here is that $\displaystyle 3\sqrt{3}$ can also be written as 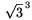$\sqrt{3}^{\,3}$ . On further investigation we hit on the pair $\displaystyle x=\root3\of{4}$ and $\displaystyle y=4\cdot\root3\of{4}$, since

$\displaystyle (4\cdot\root3\of{4})^{\root3\of{4}}=(\root3\of{4}^{\,4})^{\root3\of{4}}={\root3\of{4}}^{\,4\cdot\root3\of{4}}.$

This time the equality $\displaystyle 4\cdot\root3\of{4}=\root3\of{4}^{\,4}$ played a key role. We notice that essentially in all examples y=vx with vx=x^v is true, which will be the right track to follow.

1.1 Introducing a new variable

We look for y in the form y=vx with v being a real parameter, that is we set 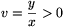$v=\frac{y}{x}>0$ . Then (1) becomes

(vx)^x=y^x=x^y=x^vx=(x^v)^x.

Since every expression here is positive, raising the leftmost and rightmost expressions to the power $\displaystyle \frac{1}{x}$, we get the crucial relation vx=x^v. Now multiplying by 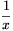$\frac{1}{x}$ we have v=x^v-1. If v $ne$ 1, that is if x$\displaystyle ne$y, raising to the power $\displaystyle \frac{1}{v-1}$ we derive 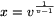$x=v^{\frac{1}{v-1}}$ . The corresponding y reads

$\displaystyle y=vx=v\cdot v^{\frac{1}{v-1}}=v^{\frac{1}{v-1}+1}=v^{\frac{v}{v-1}}=x^v.$

If v=1, then y=x.

The expression obtained for x will appear several times later on, so we set $\displaystyle h(v)=v^{\frac{1}{v-1}}$. The domain of definition of the function h is the positive reals except 1, and its range is apparently a subset of the positive reals.

We now have the possible solutions, which are actually the solutions to (1): if v=1 and x is an arbitrary positive real number, then y=x is clearly a solution, which we will call a trivial solution. If v$\displaystyle ne$1, then x=h(v) and y=v^.h(v) are nontrivial solutions, since, as we have just seen, y=vx=x^v and

y^x=(x^v)^x=x^vx=x^y.

Our first goal has been achieved by establishing that all positive real solutions (x,y) to x^y=y^x are of the form (x,x) and (h(v),v^.h(v)) (x>0,v>0,v$\displaystyle ne$1).

The function h has interesting properties. If v>0 and v$\displaystyle ne$1, then h(v) is the value which multiplied by v or raised to the power v yields the same: v^.h(v)=h(v)^v, as we have proved it. Another functional equation h satisfies is $\displaystyle v\cdot h(v)=h(\frac{1}{v})$, or equivalently 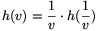$h(v)=\frac{1}{v}\cdot h(\frac{1}{v})$ , as one can easily check.

This implies for example, that nontrivial solutions can be written as $\displaystyle (h(v),h(\frac{1}{v}))$ too, consequently a solution (x,y) is transformed into the solution (y,x) by the substitution 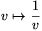$v\mapsto\frac{1}{v}$ .

The function h is not defined for v=1, nevertheless it can be shown that it is strictly decreasing and 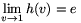$\lim_{v\to1}h(v)=e$ (with e=2.71828... being the base of the natural logarithm).

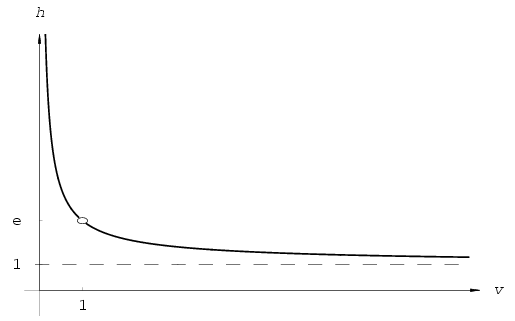
Figure 1: $\displaystyle h(v)=v^\frac{1}{v-1}$

1.2 A little calculus

We now would like to have a picture of the graph of the solutions of (1). The trivial solutions (y=x for x,y>0) are the bisector of the first quadrant in the x-y plane. The nontrivial solutions however are not of the usual form y=f(x), since y is not directly expressed in terms of x, but both x and y are functions of the parameter v. Nonetheless, it is seen that for any x from the range of h there exists exactly one y different from x such that x^y=y^x, which implies the existence of the function $\displaystyle f\colon x\mapsto y$. Using this function, nontrivial solutions can be written as (x,f(x)), namely, if h^[-1] denotes the inverse function of h (which exists because of its strict monotony), then x=h(v) implies v=h^[-1](x), hence (h(v),v^.h(v))=(x,h^[-1](x)^.x) is what we required (with f(x)=x^.h^[-1](x)). However, this manipulation will not give any further information, since expressing v from x=h(v)--that is determining the function h^[-1]--does not seem to be possible via elementary functions.

Now we investigate the behaviour of the functions h(v) and v^.h(v) in the parametric representation, from which we will able to sketch the graph of the nontrivial solutions. Plotting this graph together with the graph of the trivial solutions in the same system of coordinates yields the complete positive real solutions to (1).

We will need the concept of limit and derivative of a function (together with some well-known limits), so these proofs will be omitted, or only sketched.

To simplify things a bit--and to see some other nice relations--we again introduce a new variable: we reparametrize our coordinate functions. Let u denote the exponent in h(v), that is let $\displaystyle u=\frac{1}{v-1}$. This yields $\displaystyle v=1+\frac{1}{u}$. In terms of this new variable the two functions become

$\displaystyle h(v)=\left(1+\frac{1}{u}\right)^u$ and $\displaystyle v\cdot h(v)=\left(1+\frac{1}{u}\right)^{u+1}$.

Call these new functions of u g₁(u) and g₂(u), respectively. It is easy to see that graphs of g₁ and g₂ are reflections of each other about the axis $x=-\frac{1}{2}$ in the x-y plane, since the image of a point u of the x-axis under this reflection is (-u-1), and the substitution u$\displaystyle mapsto$(-u-1) transforms g₁ into g₂, because g₁(-u-1)=g₂(u) and g₂(-u-1)=g₁(u).

Therefore it is sufficient to examine the function g₁, properties of its counterpart g₂ will be easily deducible thereafter. Since v runs through the positive reals except 1, it is easy to see that after the substitution u will run through the set $\Bbb{R}\setminus[-1,0]$ , hence this will be the domain of definition of g₁. The behaviour of g₁ at the endpoints of its domain is established by using the following well-known limits. $\lim_{u\to+\infty}g_1(u)=e$ , from below. 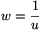$\lim_{u\to0+0}g_1(u)=1$ , from above, since the substitution $w=\frac{1}{u}$ reduces it to $\displaystyle \lim_{w\to+\infty}\root{w}\of{w+1}=1$. Further, 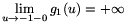$\lim_{u\to-1-0}g_1(u)=+\infty$ , since the base tends to 0 from above, while the exponent tends to (-1). Finally, 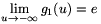$\lim_{u\to-\infty}g_1(u)=e$ from above, shown by the substitution w=-u. The function g₁ is continuous on its domain. It can be proved that it is strictly increasing on (-$\displaystyle infty$,-1) and on (0,+$\displaystyle infty$). Its graph is shown on Figure 2.

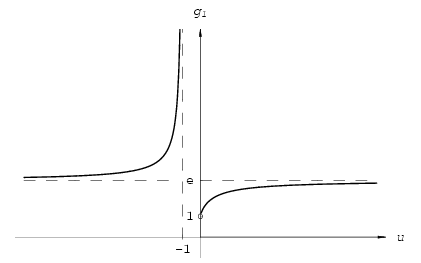
Figure 2: $\displaystyle g_1(u)=\left(1+\frac{1}{u}\right)^u$

Now we are in a position to draw the nontrivial solutions of the equation x^y=y^x from the parametrization (g₁(u),g₂(u)), $u\in\Bbb{R}\setminus[-1,0]$ , see Figure 3. (Naturally, this is equivalent to the original parametrization (h(v),v^.h(v)), v>0, v$\displaystyle ne$1.) As u increases from - $infty$ to -1, the points (g₁(u),g₂(u)) define the lower right part of the curve on the figure, since the first coordinate grows from e to +$\displaystyle infty$, while the second coordinate decreases strictly from e to 1. Conversely, as u increases from 0 to +$\displaystyle infty$, the points (g₁(u),g₂(u)) describe the upper left part of the curve, because the first coordinate grows from 1 to e, and the second coordinate strictly decreases from +$\displaystyle infty$ to e. The straight line with slope of 45^o, as we already know, comes from the trivial solutions. Thus Figure 3 contains all the positive pairs (x,y) for which the corresponding powers commute. Symmetry of the solutions manifests in the reflection symmetry of the graph with respect to the axis y=x. Trivial and nontrivial solutions meet at the point (e,e).

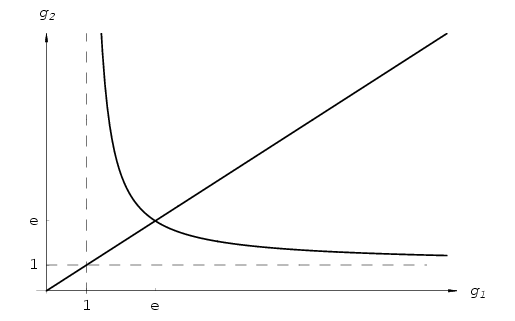
Figure 3

1.3 Some simple consequences

The analysis carried out above implies for example, that powers can not commute, if the base and the exponent are different numbers being less than 1, since in the nontrivial case g₁ and g₂ both have values strictly greater than 1. Similarly, if x,y>e and x $ne$ y, then x^y=y^x does not admit any solutions. Moreover, substituting the parametric representations into the expression x^y yields

$\displaystyle h(v)^{v\cdot h(v)}=v^{\frac{v^{\frac{v}{v-1}}}{v-1}}.$

It can be proved that the range of this function is the interval (e^e,+$\displaystyle infty$), which implies for example, that if x^y<e^e and x$\displaystyle ne$y, then x^y$\displaystyle ne$y^x.

1.4 Integer and rational solutions

After the positive real solutions, we turn our attention to the positive integer and positive rational solutions of x^y=y^x. Here again we have trivial solutions--every integer or rational x>0 with y=x is appropriate--and the more involved nontrivial ones. Integer solutions can be inferred using the graph on Figure 3: the upper left branch contains only the integer grid point (x,y)=(2,4), since the first coordinate satisfies 1<x<e, but e<3 implies x=2 (and correspondingly y=4). Due to symmetry, the only grid point on the lower right branch is (4,2). These are the integer solutions of (1).

In order to acquire rational solutions, the values of parameter v are to be determined for which both components of the pair (h(v),v^.h(v)) are positive rational numbers. If h(v) and v^.h(v) are rational, then v has to be also rational, since h(v) is positive. So we may suppose $\displaystyle v=\frac{p}{q}$ with positive integers p and q, being relatively prime. Taking into account that we are looking for nontrivial solutions, v$\displaystyle ne$1 must hold, that is p $ne$ q. As we have seen, the substitution $\displaystyle v\mapsto\frac{1}{v}$ only interchanges x and y, so it is sufficient to study the case v>1 (or equivalently, p>q), that is to inspect the upper left branch of the graph on Figure 3. So p>q$\displaystyle ge$1. Plugging $\displaystyle \frac{p}{q}$ into v, we get

$\displaystyle h(v)=\left(\frac{p}{q}\right)^{\frac{q}{p-q}}.$

Let m=p-q, then m$\displaystyle ge$1 is an integer. First we show that if m>1, then $\displaystyle h\left(\displaystyle\frac{p}{q}\right)=\root{m}\of{\frac{p^q}{q^q}}$ can not be rational. Since p and q are relatively prime, the fraction $\displaystyle \frac{p^q}{q^q}$ is also in its lowest terms. The m^th root of such a fraction can only be rational if both its numerator and denominator are perfect m^th powers.

Indeed, let $\displaystyle \root{m}\of{\frac{r}{s}}=\frac{a}{b}$, with r,s and a,b being relatively prime numbers, respectively. (r,s,a,b>0 may be assumed.) Then $\displaystyle \frac{r}{s}=\frac{a^m}{b^m}$ holds, further, a^m and b^m are relatively prime. Since the reduced form of a rational number is unique (the numerator and the denominator are positive), we conclude that both r and s are perfect m^th powers.

Hence--supposing to the contrary that 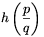$h\left(\displaystyle\frac{p}{q}\right)$ is rational--p^q=a^m and q^q=b^m hold. Now q and m are relatively prime, since p=q+m and the greatest common divisor (gcd) of p and q is 1, from which we verify that p and q are also perfect m^th powers. To this end, pick an arbitrary prime from the prime factorization of p. If its exponent is denoted by k, then its exponent in the factorization of p^q is k^.q, now divisible by m. Because the gcd of m and q is 1, we see that m divides k, therefore p is indeed a perfect m^th power. A similar argument indicates that q is also a perfect m^th power.

Now the equality m=p-q can not hold, since the difference of two different m^th powers is greater than m. Indeed, let t₁>t₂>0 be integers, then

t₁^m-t₂^m=(t₁-t₂)(t₁^m-1+t₁^m-2t₂+...+t₁t₂^m-2+t₂^m-1),

and the right hand side is strictly greater than (t₁-t₂)^.m^.t₂^m-1, which is at least m.

Thus we have proved that if m=p-q>1, then $\displaystyle h\left(\displaystyle\frac{p}{q}\right)$ is irrational.

Finally, in the case m=1 (i.e. p=q+1), $\displaystyle h(v)=\left(\frac{q+1}{q}\right)^q$ is clearly rational. Then $\displaystyle v\cdot h(v)=\left(\frac{q+1}{q}\right)^{q+1}$. Using the more usual n instead of q, we have the rational solutions as

$\displaystyle x=\left(1+\frac{1}{n}\right)^n$ and 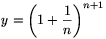$y=\left(1+\frac{1}{n}\right)^{n+1}$ ,

or vice versa, with integer n$\displaystyle ge$1. (If n=1, the formula gives the integer solution x=2 and y=4 we already have.) Therefore, these are the points of the curve on Figure 3 with both coordinates being rational.

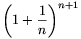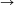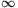The sequences $\displaystyle \left(1+\frac{1}{n}\right)^{n}$ and $\left(1+\frac{1}{n}\right)^{n+1}$ play an important role in real analysis, because they tend to the number e (as n $rightarrow$ + $infty$ ): this constant is usually defined as the limit of these very sequences. We have established another interesting property of them, namely, corresponding terms of these sequences are the only (positive and different) rational numbers for which powers x^y and y^x commute.

1.5 A different approach

In finishing the commutative case, we mention a different approach to obtain some information on the real solutions to the equation x^y=y^x. Namely, by raising both sides to the power $\displaystyle \frac{1}{xy}$ (x,y>0), we get $\displaystyle x^{\frac{1}{x}}=y^{\frac{1}{y}}$, which requires the equality of two values of the same function (not necessarily for different arguments): the original equation is equivalent to f(x)=f(y) with 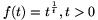$f(t)=t^{\frac{1}{t}},t>0$ .

We trivially get a solution, if x=y. The question is whether equality can hold true for x$\displaystyle ne$y. Some further analysis shows (using limits and monotony) that the function f is one-to-one on the interval (0,1], and maps the intervals (1,e) and (e,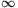 $infty$ ) onto 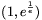$(1,e^{\frac{1}{e}})$ . (It is strictly increasing on (1,e) and strictly decreasing on (e,$\displaystyle infty$).) Using the continuity of f implies that the original equation has nontrivial solutions: for every 1<x<e there is a unique y (e<y<+$\displaystyle infty$) such that f(x)=f(y), and conversely, for every e<x<+$\displaystyle infty$ there exists a unique y (1<y<e) such that f(x)=f(y), see Figure 4. For x$\displaystyle in$(0,1] or x=e, only y=x ensures f(x)=f(y).

Summarizing, for x$\displaystyle in$(0,1] or x=e there exists a unique y, while for x$\displaystyle in$(1,e) or x$\displaystyle in$(e,+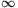 $infty$ ) there are two y's such that x^y=y^x. This approach easily yields the number of solutions, but not the solutions themselves.

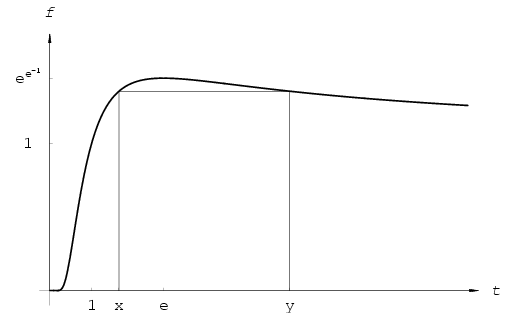
Figure 4: $\displaystyle f(t)=t^\frac{1}{t}$

2 The associative case

Our task now is to determine all positive real triples (x,y,z) for which

(x^y)^z=x^{(y^z)}.

The left hand side is clearly equal to x^yz. If x$\displaystyle ne$1, then we have yz=y^z. But this is the very equation we have encountered in the commutative case. If z=1, then every positive y is a solution, otherwise y=h(z).

Therefore we have all positive real triples for which powers are associative (see Figure 5):

(1,y,z), where y,z>0,

(x,y,1), where x,y>0,

x$\displaystyle ne$1, (x,h(z),z), where x,z>0, x$\displaystyle ne$1, z$\displaystyle ne$1.

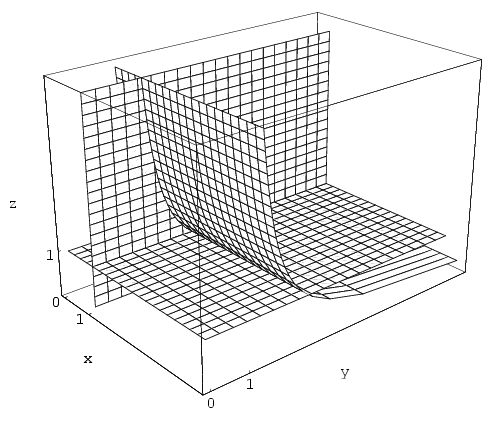
Figure 5

2.1 Integer and rational solutions

Thanks to the investigation carried out in the commutative case, rational solutions are already in our hands. Starting from the real solutions, we arrive at the conclusion that positive rational powers are associative if the triple (x,y,z) falls into one of the categories below:

(1,y,z), with rational y,z>0,

(x,y,1), with rational x,y>0, x$\displaystyle ne$1,

$\displaystyle \left(x,\left(1+\frac{1}{n}\right)^n,\frac{n+1}{n}\right)$, with rational 0<x $ne$ 1 and positive integral n,

$\displaystyle \left(x,\left(1+\frac{1}{n}\right)^{n+1},\frac{n}{n+1}\right)$, with rational 0<x $ne$ 1 and positive integral n.

The first two cases are trivial. The last two follow from the formula (x,h(z),z), since in the commutative case we have collected all rational numbers v for which h(v) is also rational. (Write z instead of v now.) There we have found that if 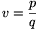$v=\frac{p}{q}$ with integers p>q$\displaystyle ge$1, then h(v) is rational if and only if p=q+1, which implies the third case (using n instead of q, and allowing q=1 also). Finally, if $\displaystyle v=\frac{p}{q}$ again, but this time with q>p $ge$ 1, then the proof in the commutative case remains true by exchanging p and q, and we get the only possibility q=p+1. This is described in the fourth row. (The case p=q has already been treated above, since here z$\displaystyle ne$1.)

As for the integer solutions, the third row above yields integer values only if n=1, but the last row never does, so the positive integer solutions to (2) are as follows:

(1,y,z), with integer y,z>0,

(x,y,1), with integer x,y>0, x$\displaystyle ne$1,

(x,2,2), with integer x>1.

Már regisztráltál?
Új vendég vagy?