Bolyai János forradalma

Prékopa András
a Magyar Tudományos Akadémia rendes tagja

A Természet Világa 2002. júliusi, augusztusi és szeptemberi számában megjelent a cikk rövidített változata.

Bolyai János a magyar tudomány legnagyobb alakja, sokan azt tartják, ő a geometria Kopernikusza. Az 1831-ben megjelent huszonhat oldalas, röviden Appendix címmel emlegetett művében (mely atyja, Bolyai Farkas kétkötetes monumentális összefoglaló munkája, a Tentamen első kötete függelékeként jelent meg) korszakalkotó eredményt ért el, létrehozta az ún. nemeuklideszi geometriát. Bolyai megtörte az euklideszi geometria egyeduralmát, felszabadította az utat az emberi gondolkodás előtt a tér másként való felfogása számára. Egyben utat nyitott a huszadik század fizikai elméletei előtt, melyek világképünket gyökeresen megváltoztatták. Bolyai a matematikatörténet egészét jelentős mértékben alakította az axiomatikus gondolkodás terén elért eredményei révén. Elmondhatjuk, hogy a modern matematika tizenkilencedik és huszadik században bekövetkezett fejlődése nagymértékben köszönhető Bolyai János munkásságának. Művének jelentőségét azonban csak halála után ismerték el, akkor sem ellenállás nélkül. Életében nem értették meg zseniális gondolatait, melyek már huszonegy éves korában megérlelődtek benne. Ezeket az ifjúság bátor forradalmiságával kifejtette, közreadta, nem félve a tudományos világ bírálatától. Ebben persze nagyfokú naivitás is volt, mert azt hitte, hogy a nagy felfedezések, mint az övé, általában elnyerik az elismerést, a felfedezők pedig a személyes dicsőséget. Aki viszont megértette Bolyai gondolatait, nevezetesen Gauss, a ,,matematikusok fejedelme'', méltatlanul viselkedett Bolyai Jánossal szemben, amikor 1832-ben az Appendixről véleményt nyilvánított. Azt írta Bolyai Farkasnak, hogy János művét nem dicsérheti, mert ez azt jelentené, hogy saját magát dicséri. Ugyanis az abban foglalt eredmények, és az út, melyen járva ezek megszülettek, szinte szó szerint megegyezik harminc, harmincöt éves meditációjával. Gauss 1855-ben bekövetkezett halála után hagyatékát feldolgozták, és említett állításának írásos bizonyítékát nem találták. Gauss későbbi magatartása is kifogásolható. Amikor tudomást szerzett arról, hogy az orosz Lobacsevszkij is felfedezte lényegében ugyanazt, mint Bolyai János - az előbbit 1842-ben megválaszttatta a Göttingeni Királyi Társaság külföldi levelező tagjának - nem tájékoztatta őt arról, hogy van még valaki más is, aki hasonló eredményeket ért el.

Hosszú ideig tartotta magát az a vélekedés, hogy Bolyai János az 1833-ban bekövetkezett nyugdíjaztatása után ugyan írt még egyet-mást, közöttük egy lényegeset is a komplex számok megalapozását illetően, de az elismerés hiánya depresszióssá tette és lényegében a matematikai alkotó munkától is visszavonult. Kiss Elemér marosvásárhelyi professzor volt az, aki erre rácáfolt, miután egy évtizedes munkával a hátrahagyott Bolyai kéziratokat átböngészte és azokban jelentős, a kéziratok keletkezésekor új ,,matematikai kincseket'' talált.

Húsz évvel ezelőtt a híres princetoni matematikus, John Milnor tollából megjelent egy cikk: ``Hyperbolic geometry: the first 150 years''. Ebben azt írja, hogy a nemeuklideszi geometria az első negyven évében bizonytalan állapotban volt. Később integrálódott a matematika tekintélyesebb ágaiba, Gaussnak a görbült felületekre és Riemannak a magasabb dimenziós görbült sokaságokra adott elmélete révén. Bár igaz, amit Milnor ír, a valóság ennél sokkal bonyolultabb.

A felületek és a magasabb dimenziós sokaságok görbületének és geometriájának az elmélete nem vezetett ki a matematikából, legalábbis nem lényegesen. A felületek görbületének az értelmezése és tulajdonságainak a vizsgálata minden további nélkül elhelyezhető volt a matematika meglévő rendszerébe. Riemann görbült sokaságaival, illetve geometriájával más a helyzet. Ebben az elméletben a geometria egy általános szemléletmódja jelent meg, ámde negyedszázaddal Bolyai és Lobacsevszkij felfedezése után. Riemann ezt az elméletet magántanári habilitációs előadásában ismertette 1854-ben. Ekkorra már kezdett világossá válni, ami Bolyai és Lobacsevszkij publikációi idejében még nem volt az, hogy ti. a geometria és a valóság lehet különböző, hogy a geometria felfogható az absztrakt elméletek egy osztályának, nem mondva le az alkalmazás igényéről, mert önkényesen is értelmezhető struktúrái ugyanolyan módon vizsgálhatók, mint pl. a függvények, vagy más matematikai objektumok. A mű egyébként Riemann halála után, 1868-ban jelent meg nyomtatásban.

Bolyai Jánosig a geometria a körülöttünk lévő valóságot írta le, attól elválaszthatatlan volt. Pont, egyenes, sík az volt, amit a szemléletünk nagy erővel ránk kényszerít. Ne feledjük, Euklidész axiómái csak a rend kedvéért születtek, hogy a fogalmak, állítások zűrzavarában el tudjunk igazodni, és tisztázzuk, mi az, ami nyilvánvaló, és mi szorul bizonyításra. A nyilvánvaló állítások, axiómák pedig a lehető legkevesebben legyenek, ne tekintsünk axiómának olyan állítást, mely a többiből levezethető.

Bolyai János felfedezése előtt a matematikusok azt várták, hogy jön egy zseni, aki a többi axiómára támaszkodva ragyogó bizonyítást ad az V. posztulátumra. Hiszen még a közvetlen elődök, Saccheri és Lambert is csak azért tételezték fel az V. posztulátum nem igaz voltát, hogy indirekt bizonyítást alkalmazva, ellentmondásra jussanak. A világ ugyanis euklideszi. Ezt nem így mondták, de így gondolták. A kor legnagyobb filozófusától, Immanuel Kanttól kezdve az utca emberéig ez volt a meggyőződés. Ma már tudjuk, hogy a relativitáselmélet mást tanít és kísérleti bizonyítékok is szólnak mellette, de ezt is csak a műveltebbek tudják. Napi életünk, tevékenységünk az euklideszi geometriára támaszkodik. A gyerek, amikor füzetét megvonalazza, a földmérő, amikor kiméri telkünket, nem kell, hogy azzal törődjön, vajon húzható-e több párhuzamos adott egyeneshez egy rajta kívül fekvő ponton át.

Bolyai a geometriát az absztrakt elméletek világába helyezte át. Megmutatta, hogy logikailag egynél több geometria is lehetséges. Ahogy 1823. november 3-án Temesvárról apjának írta: ,,a semmiből egy ujj, más világot teremtettem''. Egy elgondolt világot, természetesen.

Az 1823. november 3-i levél után Bolyai német nyelven leírta eredményeit és a dolgozatot 1826-ban odaadta egykori bécsi tanárának, akkori aradi elöljárójának, Johann Wolter von Eckwehrnek. A kézirat azonban elveszett. Apja buzdítására művét latin nyelven is megírta, amely azután Bolyai Farkas Tentamen című kétkötetes monumentális műve első kötete Appendixeként jelent meg. Teljes címe: Appendix, Scientiam Spatii absolute veram exhibiens; a veritate aut falsitate Axiomatis XI. Euclidei (a priori haud unquam decidenda) independentem; adjecta ad casum falsitatis quadratura circuli geometrica. Magyarul: Appendix, A Tér abszolút igaz Tudománya, a XI. Euklidész-féle axióma (a priori soha el nem dönthető) helyes, vagy téves voltától független tárgyalásban; annak téves volta esetére a kör geometriai négyszögesítésével.

Bolyai János nem kísérletezett azzal, hogy művét a kor vezető matematikai folyóiratai valamelyikében publikálja. Ehhez ugyan apjának Gauss segítségével meglett volna a kapcsolata, de a gondolat nem merült fel. Talán János szerencséjére, mert, mint tudjuk, Gauss az 1831-ben neki megküldött Appendixszel kapcsolatban levelet írt Farkasnak, mely Jánosra lesújtó hatással volt. Az Appendixben foglalt eredményekről ugyan elismeréssel nyilatkozott, de azt is írta, hogy ezekre már ő is rájött.

Az Appendix sok magyar és idegen nyelvű kiadásban megjelent. Angolra a texasi George Bruce Halsted fordította 1891-ben, mely a fordító előszavával Bonola eredetileg olasz nyelven írt könyvének angol fordításában (1911) is megjelent. Az Appendix eredeti változata (címlapot stb. nem számítva) huszonnégy oldalas mű. Erről Halsted professzor előszavában azt írja, hogy ,,ez a huszonnégy oldal a legrendkívülibb két tucat oldal a gondolkodás történetében''. Nos, ne csak dicsérjük Bolyai Jánost, hanem ismerkedjünk is meg az Appendix néhány jellegzetes eredményével.

Említettük, hogy Bolyai még Euklidész axiómarendszerén belül gondolkodott, a teljesebb, Hilbert-féle axiómarendszer csak 1899-ben látott napvilágot. Ami azonban Bolyainak az Appendixben alkalmazott levezetéseit és általában módszertanát illeti, e tekintetben felhasználta az elmúlt századok nagy újításait, mindenekelőtt Descartes analitikus geometriáját, továbbá Newton és Leibniz differenciál- és integrálszámítását. Az előbbi bizonyos értelemben az egzaktság egy új, magasabb szintjét is jelentette, nem csupán azt, hogy algebrai eszközökkel is lehetségessé vált geometriai problémák megoldása.

Euklidész V. posztulátumát a következő módon lehet megfogalmazni: ha a síkon adott egy l egyenes és egy rajta kívül fekvő P pont, akkor egy és csakis egy olyan egyenes van, amely tartalmazza a P pontot és párhuzamos az l egyenessel. Ezt az ekvivalens megfogalmazást Playfair (1748-1819) adta meg.

Bolyai először, elvetve az V. posztulátumot (mely nála a XI. axióma nevet viseli), értelmezi a párhuzamosságot. Tekintsünk egy l egyenest és egy rajta kívül fekvő P pontot. Ha a P pontból kiindulva egy félegyenest húzunk, amely metszi az l egyenest az egyik irányban, majd a metszéspontot fokozatosan kitoljuk a végtelenbe, akkor lesz egy olyan határeset, amikor a félegyenes már nem metszi l-et (1. ábra). Ugyanezt a másik irányba menve is megtehetjük. A határhelyzetű félegyeneseket hosszabbítsuk meg a másik irányba is, kapunk két olyan egyenest, melyek párhuzamosak l-lel. Ha a két egyenes különbözik, akkor közöttük végtelen sok egyenes helyezkedik el, melyeket szintén párhuzamosaknak nevezhetünk, ezek azonban a határegyenesektől eltérő tulajdonsággal rendelkeznek. Az ennek az esetnek megfelelő geometriát hiperbolikus geometriának nevezzük.

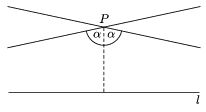
1. ábra. Elpattanó egyenesek

Ezen a ponton megjegyezzük, hogy Bolyai egyenesei nem feltétlenül ,,egyenesek'' a köznapi értelemben, a szemléltető ábrákon mégis köznapi értelemben vett egyeneseket rajzolunk. A Bolyai-Lobacsevszkij geometria ,,egyenesei'' félkörök vagy más geometriai objektumok is lehetnek.

Bolyai kiépítette az V. posztulátumtól független abszolút geometriát. Az alábbi tétel az abszolút síkgeometria körébe tartozik. Ha a P pont az l egyenestől d távolságra van, és a P pontból az l egyenesre bocsátott merőleges és a határhelyzetű párhuzamos által bezárt szög $\alpha$ , akkor érvényes Bolyai formulája:

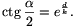
$\mathop{\rm ctg}\frac{\alpha}{2}=e^{\frac{d}{k}}.$

Az ebben a formulában szereplő k állandó univerzális független attól, hogy mely l egyenest és P pontot vesszük. Ugyanez a k fordul elő más geometriai mérőszámok képletében is Bolyai geometriájában.

Bolyai kiépítette a hiperbolikus trigonometriát, és alkalmazta a felszín és a köbtartalom meghatározására. Ez utóbbi rendkívül érdekes. Pl. az r sugarú kör kerülete a hiperbolikus geometriában az alábbi értékkel egyenlő:

$\displaystyle \pi k\left(e^{\frac{r}{k}}-e^{-\frac{r}{k}}\right)=2\pi k\mathop{\rm sh}\frac{r}{k}, $

ahol k a már ismert, az egész térre nézve univerzális állandó. Ezt későbbi matematikai művekben a tér görbületének reciprokával fogják azonosítani. Ha 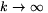$k\to\infty$ , akkor a fenti formula határeseteként 2r $\pi$ adódik, ami a kör kerületének jól ismert képlete az euklideszi geometriában.

Bolyai János egyik legszebb, az abszolút geometriában érvényes tétele a következő: Egy háromszög szögeinek szinuszai úgy aránylanak egymáshoz, mint azoknak a köröknek a kerületei, amelyeknek sugarai rendre megegyeznek a szemben lévő oldalakkal. Ha a szögeket A, B, C; a szemben lévő oldalakat a, b, c; az r sugarú kör kerületét Or jelöli, akkor tehát Bolyai tétele a

Oa: O b : Oc = sin A:sin B:sin C

formulával fejezhető ki. Az euklideszi geometriában Or= 2 $\pi$ r, a fenti formula tehát az ismert a:b:c = sin A:sin B:sin C alakot ölti. A hiperbolikus geometria esetében viszont

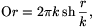
$\mathrm{O}r=2\pi k\mathop{\rm sh}\frac{r}{k},$

amiből következik, hogy

$\displaystyle \mathop{\rm sh}\frac{a}{k}:\mathop{\rm sh}\frac{b}{k}:\mathop{\rm sh}\frac{c}{k} =\sin A:\sin B:\sin C. $

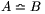Tekintsünk most két párhuzamos egyenest: a, b, és vegyünk fel mindegyiken egy pontot: A, B. Az egyeneseknek iránya is van, amint korábban említettük, ezeket jelöljék M, N (2. ábra). Tételezzük fel, hogy az MAB szög egyenlő az NBA szöggel. Ekkor az A és B pontokat izogonális korreszpondáló, vagy röviden korreszpondáló pontoknak nevezzük (ez Gauss elnevezése), és a tényt az $A\bumpeq B$ relációval juttatjuk kifejezésre (Bolyai János jelölése). Ez a reláció független az V. 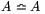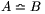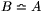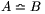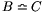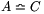posztulátumtól, az abszolút geometria körébe tartozik, és rendelkezik a reflexív, szimmetrikus és tranzitív tulajdonságokkal: $A\bumpeq A$ ; ha $A\bumpeq B$ , akkor $B\bumpeq A$ ; ha $A\bumpeq B$ és $B\bumpeq C$ , akkor $A\bumpeq C$ .

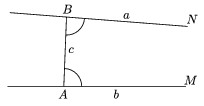
2. ábra. Korreszpondáló pontok

Ha egy reláció rendelkezik a fenti tulajdonságokkal, akkor azt ekvivalencia relációnak nevezzük. Ismeretes, hogy egy tetszőleges halmazon belül egy, az elemekre vonatkozó ekvivalencia reláció megvalósít egy páronként közös elem nélküli részhalmazokra történő felosztást. Ezeket ekvivalencia osztályoknak nevezzük.

Mármost az izogonális korreszpondencia reláció által létesített mindegyik ekvivalencia osztály egy síkbeli ponthalmaz, melyen belül - amint Bolyai ezt kimutatja - az euklideszi geometria érvényes. Ezeket horociklusoknak nevezzük.

Hasonlóan értelmezhető a horoszféra fogalma. A horoszférán belül szintén az euklideszi geometria érvényes. A horociklus, horoszféra végtelen sugarú körnek, ill. gömbnek tekinthető.

Ha egy háromszög szögei $\alpha$ , $\beta$ , $\gamma$ , akkor az euklideszi geometriában $\alpha$ + $\beta$ + $\gamma$ = $\pi$ , a hiperbolikus geometriában azonban $\alpha$ + $\beta$ + $\gamma$ < $\pi$ . A két szám $\pi$ -( $\alpha$ + $\beta$ + $\gamma$ ) különbségét a háromszög defektusának nevezzük. Bolyai bebizonyította, hogy a háromszög $\Delta$ területe egyenlő az alábbi mennyiséggel:

$\Delta$ = k² ( $\pi$ - ( $\alpha$ + $\beta$ + $\gamma$ )),

ahol k a már ismert univerzális állandó. Ezt a formulát Lambert is ismerte, Bolyai viszont szabatosan be is bizonyította.

Bolyai egy további érdekes tétele a következő: egy derékszögű háromszög a, b befogóira és c átfogójára (a szög az ,,egyenesek'' metszéspontjában található szöget jelenti) érvényes az alábbi formula:

$\displaystyle \mathop{\rm ch}\frac{c}{k}=\mathop{\rm ch}\frac{a}{k} \mathop{\rm ch}\frac{b}{k}. $

Ha 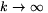$k\to\infty$ , akkor határesetként a c²=a²+b² formulát kapjuk, ami Pitagorasz tétele.

Bolyai Farkas a Tentamenben néhány oldalon megjegyzéseket fűzött az Appendixhez. Ezek között részletesebb levezetést ad a fenti határértékrelációra.

Végül megemlítjük, hogy Bolyai az Appendixben foglalkozik a hiperbolikus geometrián belüli szerkesztésekkel is.

Bolyai János egyéb matematikai munkásságáról Stäckel Pál (1914), Dávid Lajos (1979), Bolyai János (szerk. Kárteszi Ferenc 1977), Weszely Tibor (1981) és Kiss Elemér (1999) ad jó áttekintést. Hatásáról a geometria fejlődésére Varga Ottó (1953) cikke tartalmaz fontos információt. Milnor (1982) már említett cikke az utolsó összefoglaló mű a hiperbolikus geometria terén elért eredményekről. Bolyai János nem matematikai jellegű írásainak kiadása és értékelése folyamatban van.

A nemeuklideszi geometria másik nagy felfedezője az orosz Lobacsevszkij (1793-1856). Bolyai és Lobacsevszkij munkája között a különbség röviden úgy fogalmazható meg, hogy Bolyai kiépítette az abszolút geometriát is, Lobacsevszkij viszont részletesebben dolgozta ki a hiperbolikus trigonometriát. Nem sok értelme van a kettejük közötti prioritási vitának. Hogy mégis lássunk valamit e tekintetben, megemlítjük a következőket.

Lobacsevszkij első, a nemeuklideszi geometriáról szóló publikációi 1829-1830-ban jelentek meg orosz nyelven a Kazanyi Hírmondóban. Bolyai Appendixe különnyomatként 1831-ben jelent meg, az egész Tentamen imprimatúrájának éve azonban 1829. Bolyairól tudjuk, hogy 1823-ban már nagy vonalakban felépítette geometriáját és 1826-ban művének német nyelvű változata el is készült. Minthogy az utóbbi elveszett, az előbbi pedig csak levélbeli bejelentése a felfedezésnek, nem állnak rendelkezésre az Appendix megjelenéséhez képest korábbi keletű dokumentumok Bolyai felfedezését illetően. Másfelől Lobacsevszkijjel kapcsolatban is lehet hivatkozni arra, hogy 1826-ban tartott egy témába vágó előadást a kazányi egyetemen. Ha viszont ennek címét tüzetesen megnézzük, akkor láthatjuk, hogy az előadó ekkor még az V. posztulátumot szándékozik bizonyítani (Kiss Elemér, 1999).

Több szerző szerint a Bolyai-Lobacsevszkij-féle geometria a kantiánus térszemlélet bírálatát, egyesek szerint cáfolatát is eredményezte. Azzal érvelnek, hogy ha tudatunkban egyaránt megfér egymással az euklideszi és a hiperbolikus geometria, akkor nem lehetséges az, hogy a térről a priori fogalmunk legyen, az objektumokról szerzett tapasztalattól függetlenül.

Az kétségtelen, hogy az euklideszi geometria abszolutizálása a kantiánus filozófiában vakvágánynak bizonyult, nem annyira a Bolyai-Lobacsevszkij-féle geometria, hanem a huszadik századi fizikai eredmények miatt. Kantnak az a nézete azonban, hogy a tér euklideszi, különválasztható a térre vonatkozó egyéb nézeteitől, melyek árnyaltabbak és különbözők attól, ami a fenti ellenvetésből kiolvasható. Kant nem tagadta, hogy a térről több absztrakt matematikai elmélet is megfogalmazható.

Mindamellett Gauss, Bolyai és Lobacsevszkij korában a kantiánus filozófia az euklideszi geometria szilárd támogatójának számított. Ha Gauss félt a beociaiak támadásától (akiket az athéniek élvhajhász, buta embereknek tartottak), hogy eredményeit közzétegye, nem félt ettől sem Bolyai, sem Lobacsevszkij. Mindketten forradalmárok voltak, tudományos meggyőződésüket bátran tárták a világ elé.

Hivatkozások

[1] Benkő S. (1968). Bolyai János vallomásai. Irodalmi Könyvkiadó, Bukarest. Második kiadás: Kriterion Könyvkiadó, Bukarest, 1972.

[2] Benkő S. (1978). Apa és fiú (Bolyai tanulmányok). Magvető Könyvkiadó, Budapest.

[3] Bolyai Farkas (1832-1833). Tentamen juventutem studiosam in elementa matheseos purae, elementaris ac sublimioris, methodo intuitiva, evidentiaque huic propria, introducendi. Cum Appendice triplici. I., II. Maros Vásárhely.

[4] Bolyai Joannes (1831). Appendix, Scientiam Spatii absolute veram exhibens; a veritate aut falsitate axiomatis XI. Euclidei (a priori haud unquam decidenda) independentem; adjecta ad casum falsitatis quadratura circuli geometrica. Maros Vásárhely.

[5] Bolyai János (1977). Appendix, a tér tudománya (szerk. Kárteszi Ferenc). Akadémiai Kiadó, Budapest.

[6] Bonola, R. (1911). Non-Euclidean Geometry. Dover, New York.

[7] Dávid L. (1979). A két Bolyai élete és munkássága. Második, bővített kiadás. Gondolat, Budapest.

[8] Euklidész (1983). Elemek. Gondolat, Budapest.

[9] Kiss E. (1999). Matematikai kincsek Bolyai János kéziratos hagyatékából. Akadémiai Kiadó, Budapest.

[10] Lobacsevszkij, N. I. (1951). Geometriai vizsgálatok a párhuzamosok elméletének köréből (V. F. Kagan bevezetésével, magyarázataival és függelékével). Akadémiai Kiadó, Budapest.

[11] Milnor, J. (1982). Hyperbolic geometry: The first 150 years. Bull. (New Series) Amer. Math. Soc., 6, 9-24.

[12] Stäckel, P. (1914). Bolyai Farkas és Bolyai János geometriai vizsgálatai I-II. Budapest.

[13] Varga O. (1953). A Bolyai-Lobacsevszkij geometria hatása a geometria fejlődésére. MTA Mat. Fiz. Tud. Oszt. Közl., 3, 151-171.

[14] Weszely T. (1981). Bolyai János matematikai munkássága. Kriterion, Bukarest.

Már regisztráltál?
Új vendég vagy?