A KöMaL 2009. decemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2010. január 11-én LEJÁRT. |
I. 226. A sok munkatárssal működő intézményekben költségtakarékosságból sok kis nyomtató helyett inkább néhány nagy kapacitásút használnak. Előnyt jelent a nyomtató nagyobb tudása, sebessége, alacsony üzemeltetési költsége. Egyetlen számottevő hátránya van: ha többen akarnak közel egy időben nyomtatni, akkor bizony várni kell. A papírkifogyás okozta időveszteséget két, egyenlő méretű papíradagoló tálcával oldják meg. (A két tálca között automatikusan, időveszteség nélkül vált a nyomtató, az üres tálcát azonnal újratöltik.)
A beérkező nyomtatási igényeket az egyik munkanap a feladat.txt állományban rögzítik a beérkezés sorrendjében. Az első sor első száma megadja, hogy a nyomtató egy lapot hány másodperc alatt nyomtat ki, a második szám pedig a papíradagoló tálcák külön-külön vett kapacitását jelöli. A további sorokban a nyomtatási feladat beérkezésének ideje (óra, perc, másodperc), a nyomtatandó oldalak száma és a nyomtatást kérő neve szerepel. Az oldalszám értéke legfeljebb 100 lehet. A cégnél legfeljebb kéttucatnyian dolgoznak.
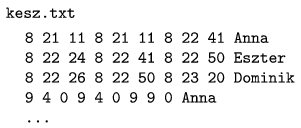
Például:

A 4. sor megmutatja, hogy a feladat Dominiktól 8:22:26-kor érkezett, amelyben 10 lap nyomtatását kéri. Ezen nyomtatási feladat végrehajtása 30 másodpercet igényel.
Készítsünk programot nyomtat néven, amely az alábbi kérdésekre válaszol. Ügyeljünk arra, hogy programunknak minden helyes tartalmú bemeneti állomány esetén működnie kell.
Minden részfeladat megoldása előtt írjuk a képernyőre a feladat sorszámát. Ha a felhasználótól kérünk be adatot, jelenítsük meg a képernyőn, hogy milyen értéket várunk (például a 2. feladat esetén: ,,2. feladat: Adja meg egy dolgozó nevét.''). A képernyőn megjelenített üzenetek esetén az ékezetmentes kiírás is elfogadott.
1. Olvassuk be a feladat.txt állományban talált adatokat, s azok felhasználásával oldjuk meg a következő feladatokat. Ha az állományt nem tudjuk beolvasni, az első 10 csomaghoz tartozó adatokat jegyezzük be a programba és dolgozzunk azzal.
2. Kérjük be a felhasználótól egy dolgozó nevét, majd írjuk a képernyőre, hogy az illető mikor küldött nyomtatási feladatot. Minden időpont új sorban jelenjen meg óra:perc:másodperc formában.
3. Készítsünk statisztikát, hogy az egyes órákban hány feladat érkezett. Az eredményt (az órát és a darabszámot) soronként írjuk a képernyőre. A nyomtatási feladatot nem tartalmazó órákat ne jelenítsük meg.
4. Adjuk meg azon dolgozók nevét, akik a vizsgált napon 9 óra előtt már nyomtattak. A neveket egymástól egy-egy szóközzel elválasztva, ábécé-rendben írjuk a képernyőre.
5. Listázzuk ki, mely nyomtatási feladatok megoldása közben váltott adagolót a nyomtató. A feladatok sorszámát egy-egy szóközzel elválasztva jelenítsük meg a monitoron.
6. Készítsünk kimutatást, amely feladatonként tartalmazza a feladat beérkezésének, a nyomtatás elkezdésének és a befejezésének idejét valamint a dolgozó nevét. Az adatokat soronként a kesz.txt állományba jegyezzük be.
Beküldendő a program forráskódja (i226.pas, i226.cpp, ...), valamint a program rövid dokumentációja (i226.txt, i226.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható egy tömörített i226.zip állományban.
Forrásfájl: feladat.txt
(10 pont)
I. 227. Oldjuk meg táblázatkezelő segítségével egy háromfordulós verseny eredményének kiszámítását. A versenyen minden fordulóban három-három feladatot kell a versenyzőknek megoldani, amely feladatok mindegyikére legföljebb 10 pont kapható. A kapott pontok alapján a versenyzők az egyes fordulókban helyezéspontokat szereznek, melyekből végül az alábbi leírás szerint kialakul a verseny eredménye.
Minden adatot és számítást a Verseny nevű munkalapra helyezzünk el. A munkalap A1:J1 tartomány minden cellájába egy-egy vezetéknevet, az alattuk lévő cellákba pedig egy-egy keresztnevet írjunk be. Az A6:A25 cellákba képezzünk a vezeték- és keresztnevek felhasználásával véletlenszerűen neveket -- ők indultak a versenyben. Az A5:K5 tartomány celláinak tartalma rendre Név; I/1. feladat; I/2. feladat; ...; III/3. feladat; Eredmény legyen. A B6:J25 cellákba véletlenszerűen helyezzünk el 0--10-ig egész számokat -- a versenyzők feladatokra kapott pontszámait.
A K6:K25 tartomány celláiba a verseny összesített eredménye alapján adjuk meg az indulók értékelését. Az értékelés az alapján történik, hogy az egyes versenyzők fordulónként pontszámaik összesítése alapján hányadik helyezést értek el az adott fordulóban. Bármely forduló győztese(i) egy helyezéspontot, a második helyezett(ek) két helyezéspontot, stb. kapnak az adott fordulóban. Ezután a három fordulóban kapott helyezéspontok összegét képezzük. Ebből levonunk minden olyan indulónál feladatonként 5-öt, aki az adott feladatot egyedül oldotta meg maximális pontszámmal. Ugyanakkor minden olyan indulónál feladatonként 5-öt hozzáadunk az összeghez, ahol az induló a feladatot nem oldotta meg (tehát az adott feladatra 0 pontot kapott). Az így módosított helyezéspont szerint növekvő sorrendet véve alakul ki az indulók értékelése: a legkevesebb helyezéspontot elérő(k) 1. díjat, a második legkevesebb helyezéspontot elérő(k) 2. díjat, és a harmadik legkevesebb helyezéspontot elérő(k) 3. díjat kapnak, tehát ez a szöveg jelenjen meg a K oszlop megfelelő sorában. Ezen kívül a következő legjobb három helyezéspontot szerző induló(k) mind Dicséretet kapnak értékelésként a K oszlop megfelelő sorában.
A megoldás során csak képletek és a táblázatkezelő beépített függvényei használhatók, saját függvények és makrók nem. Az eredmények számításakor a Verseny munkalapot használjuk, minden segédszámítást a 30-adik sortól lefelé helyezzünk el.
Beküldendő egy tömörített állományban (i227.zip) a táblázatkezelő munkafüzet (i227.xls, i227.ods, ...), illetve egy rövid dokumentáció (i227.txt, i227.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziója, valamint a megoldás rövid leírása.
(10 pont)
I. 228. A következő játékot ketten játszhatják. Egy sorba felállítanak páros sok bábut, amelyek mindegyikének ismert a tömege. A játékosok felváltva vesznek el a sor valamelyik végéről egy-egy bábut. Amikor a bábuk elfogynak, a levett bábuk tömegét összeadják és az nyert, akinél az összeg nagyobb.
Készítsük el a játék weblapon játszható változatát. Jelenítsük meg egy lapon a bábuk képét és rajtuk vagy alattuk a bábu tömegét. Ha a felhasználó a kívánt bábura kattint, és az a sor végén található, akkor a program tüntesse el a bábut, tömegét pedig adja hozzá a játékos eredményéhez. Amikor az összes bábu elfogyott, a program nevezze meg a győztest. Az egyik játékos legyen a gép, aki a játékot kezdi.
A játékot 16 bábura kell elkészíteni. A gép stratégiája, amely egyben a nyerés algoritmusa a következő: a kezdő játékos összeadja a páros és a páratlan sorszámú bábuk tömegét és azokból veszi le a sor végén állót, amelyik tömege nagyobb. Egyenlőség esetén mindegy, hogy a páros vagy páratlan sorszámúakat szemeli ki.
A feladat megoldásánál a HTML és a JavaScript elemei használhatók.
Beküldendő az i228.html dokumentum és az esetlegesen szükséges GIF, JPEG vagy PNG formátumú képfájlok, valamint a megoldás rövid dokumentációja (i228.txt vagy i228.pdf) egy i228.zip fájlba tömörítve.
(A feladat alapjául az 1996-os Nemzetközi Informatikai Diákolimpia egyik feladata szolgált.)
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2010. január 11-én LEJÁRT. |
S. 49. Bergengócia környezettudatos ország. Azt tervezik, hogy a teherszállítást hidrogénnel hajtott járművekkel oldják meg. A hidrogént cseppfolyósítva lehet - a benzinhez hasonlóan - nagybiztonságú tárolótartályokból a teherautókba tölteni. Sajnos még kevés töltőállomás van. Hidrogén üzemanyagú teherszállítást ott lehet alkalmazni, ahol a hidrogénkutak legfeljebb \(\displaystyle K\) kilométer távolságban vannak egymástól.
A bergengócok pontosan nyilvántartják a hidrogénkutak koordinátáit. Két kút távolságán a koordináta-különbségek abszolút értékének összegét értik:
\(\displaystyle T= |x_1 -x_2|+ |y_1 -y_2|. \)
Segítsük a bergengóc teherszállítás tervezőit azzal, hogy a hidrogénkutakat csoportosítsuk. Két kutat egy csoportba teszünk, ha az egyiktől a másikig el lehet jutni a csoport kútjait érintve úgy, hogy az egymást követő kutak távolsága legfeljebb \(\displaystyle K\) kilométer.
Készítsünk programot, amely megadja, hogy a hidrogénkutak hány csoportot alkotnak és melyek tartoznak egy csoportba.
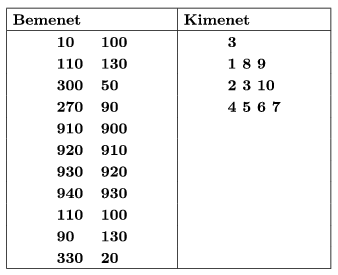
A program a parancssor első argumentumaként megadott bemeneti állomány első sorából beolvassa a hidrogénkutak \(\displaystyle N\) (\(\displaystyle 3\le N\le 200\)) számát, \(\displaystyle K\) (\(\displaystyle 100\le K\le 500\)) távolság értékét, majd a következő \(\displaystyle N\) sorból a kutak \(\displaystyle x\); \(\displaystyle y\) (\(\displaystyle 0\le x;y\le 1000)\) koordinátáit.
A parancssor második argumentumaként megadott kimeneti állomány első sorába írjuk a csoportok \(\displaystyle DB\) számát, majd a következő \(\displaystyle DB\) sorba az egy csoportba tartozó hidrogénkutak sorszámát szóközzel elválasztva.
Beküldendő egy tömörített állományban (s49.zip) a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét bemutató dokumentáció.
Forrásfájlok: S49teszt.zip
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

