A KöMaL 2011. szeptemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2011. október 10-én LEJÁRT. |
K. 295. Hány jegyű a 2011201020092008...10987654321 szám? Osztható-e ez a szám 3-mal?
(6 pont)
K. 296. Egy sorozat első tagja 2011. A második tagtól kezdve minden tag megegyezik az őt megelőző tagnál 2-vel nagyobb szám reciprokának (-2)-szeresével. Mennyi a sorozat 2011. tagja?
(6 pont)
K. 297. Az ábrán látható módon egy téglalap jobb felső sarkából kivágtunk egy négyzetet. Az így kapott síkidom területe 2011 cm2.
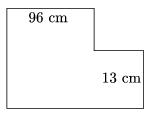
Mekkora az eredeti téglalap területe?
(6 pont)
K. 298. Egy négyszög három szomszédos oldalának hossza megegyezik, a négyszög általuk meghatározott két belső szöge pedig 60o, illetve 70o.
Mekkora a négyszög legnagyobb szöge?
(6 pont)
K. 299. Egy városban 2011 ikerpár lakik. A 4022 ember között 1900 fiú van, és a lány--lány ikerpárok száma 11-gyel több, mint a fiú--lány ikerpárok száma.
Hány fiú--fiú ikerpár van a városban?
(6 pont)
K. 300. Néhány lánybarátnő, akiknek a haja szőke, barna, vagy fekete, együtt ment nyaralni. Közülük 3 kivételével mind szőke, 4 kivételével mind barna, 5 kivételével mind fekete hajú.
Hányan vannak a nyaraló barátnők?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2011. október 10-én LEJÁRT. |
C. 1085. Adott n darab pénzérme írással felfelé. Minden egyes lépésben n-1 darabot megfordítunk. Elérhető-e, hogy mindegyik érmén a fej legyen felül?
(5 pont)
C. 1086. Egy derékszögű háromszögben a derékszög hosszúságú szögfelezője az átfogót harmadolja. Számoljuk ki az átfogóhoz tartozó magasság hosszát.
(5 pont)
C. 1087. Egy számtani sorozat első eleme 1, második eleme n, első n elemének összege pedig 33n. Határozzuk meg n értékét.
(5 pont)
C. 1088. Egy derékszögű háromszög alapú egyenes hasáb minden élének hossza egész szám. A hasábnak van 30 és 13 területű lapja. Mekkora a térfogata?
(5 pont)
C. 1089. A pozitív körüljárású ABCD négyszög területe 20, három csúcsának koordinátái A(-2;0), B(2;0) és C(2;4). Mennyi az ABCD négyszög kerületének minimuma?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2011. október 10-én LEJÁRT. |
B. 4372. Mutassuk meg, hogy ha n pont úgy helyezkedik el, hogy bármely négy közül kiválasztható három, amelyek egy egyenesre esnek, akkor a pontok közül legalább n-1 kollineáris.
(3 pont)
B. 4373. A soklábú lények nemzetközi konferenciája az Üveghegy tetején kerül megrendezésre. A résztvevőknek rendre a1,...,an lábuk van, valamennyi pozitív páros szám. Az Üveghegy csúszós, a hegy lábánál gyülekező lények csak akkor juthatnak fel a hegyre, ha lábaik számának legalább felére speciális mászócipőt húznak. Tudván, hogy mászócipő csak lábon hordva juthat fel a hegyre és onnan vissza, legalább hány cipő szükséges a konferencia résztvevőinek a feljutáshoz?
Javasolta: Mészáros Gábor (Kemence)
(4 pont)
B. 4374. Egy 5 cm élhosszúságú kocka alakú sajt közepén ül Pacworm, a sajtkukac. A sajtot úgy rágja meg, hogy mindig egyszerre 1 cm-t halad valamelyik éllel párhuzamosan, majd irányt vált figyelve arra, hogy amikor elindul az új irányba, akkor több mint 1 cm vastagságú érintetlen sajtréteg legyen előtte. Feltéve, hogy mind elindulásnál, mind irányváltásnál a sajtkukac a lehetséges irányok közül ugyanakkora valószínűséggel választ ki egyet, mekkora a valószínűsége annak, hogy 5 cm megtétele után valamelyik éltől legfeljebb 0,8 cm távolságra lesz?
(4 pont)
B. 4375. Legyen egy derékszögű háromszög két befogója a és b, valamint a c átfogóhoz tartozó magasság m. Melyik a nagyobb a következő szakaszok közül: a+b vagy m+c?
Javasolta: Székely Péter (Budapest)
(3 pont)
B. 4376. Igazoljuk, hogy ha x, y nemnegatív számok, akkor
Javasolta: Szoldatics József (Dunakeszi)
(4 pont)
B. 4377. Az ABC háromszög oldalaira kifelé megszerkesztjük az ABD, BCE, CAF szabályos háromszögeket. Legyenek a DE, EF, FD szakaszok felezőpontjai rendre G, H, I. Igazoljuk, hogy BG=CH=IA.
Javasolta: Miklós Szilárd (Herceghalom)
(4 pont)
B. 4378. Legyen p pozitív prímszám. Oldjuk meg az egész számok halmazán az
x3y3+x3y2-x2y3+x2y2-x+y=p+2
egyenletet.
Javasolta: Bíró Bálint (Eger)
(5 pont)
B. 4379. Szerkesszük meg a nem egyenlő szárú háromszöget, ha adottak a külső szögfelezőknek a körülírt körrel vett, csúcsoktól különböző metszéspontjai.
(4 pont)
B. 4380. Egy konvex k-szög oldalain felveszünk m pontot úgy, hogy az így kapott n=k+m elemű ponthalmaz középpontosan szimmetrikus alakzat legyen. Igazoljuk, hogy a
pontjai által meghatározott
szakasz között legfeljebb 2n-3 lehet ugyanolyan hosszú. Mely
halmazok esetén található 2n-3 darab ugyanolyan hosszú szakasz?
(5 pont)
B. 4381. Adott három, páronként kitérő egyenes. Hol helyezkedhet el a középpontja egy olyan paralelepipedonnak, amelynek az egyenesek mindegyikére illeszkedik éle?
(4 pont)
 |
A-jelű feladatokA beküldési határidő 2011. október 10-én LEJÁRT. |
A. 539. Keressük meg azokat a p 3 prímszámokat, amelyekre 1+k(p-1) minden
3 prímszámokat, amelyekre 1+k(p-1) minden egész számra prím.
Kolmogorov kupa, 2010
(5 pont)
A. 540. Az A1A2A3 nem szabályos háromszög magasságpontja M, Feuerbach-pontja F, körülírt köre k. Minden egyes i=1,2,3-ra legyen ki az a kör, ami belülröl érinti k-t, továbbá érinti az AiAi+1 és AiAi+2 oldalakat (Az indexet modulo 3 értjük, tehát A4=A1 és A5=A2.) A k és a ki körök érintési pontját jelöljük Ti-vel. Bizonyítsuk be, hogy az A1T1, A2T2, A3T3 és MF egyenesek egy ponton mennek át.
(A Feuerbach-pont az a pont, ahol a háromszög Feuerbach-köre és beírt köre érintik egymást.)
Javasolta: Damásdi Gábor és Mester Márton (Budapest)
(5 pont)
A. 541. A H halmaz elemei olyan véges sorozatok, amelyek elemei 1, 2 és 3 közül kerülnek ki, továbbá egyik H-beli sorozat sem részsorozata egyetlen másik H-beli sorozatnak sem. Igazoljuk, hogy H véges. (Az sorozat részsorozatai az (ai1,...,aik) alakú sorozatok, ahol 0
 k
k n és
n és .)
Javasolta: Pongrácz András (Budapest)
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

