A KöMaL 2013. januári informatika feladatai

I-jelű feladatok A beküldési határidő 2013. február 11-én LEJÁRT.

---

I. 310. Jégtáblákat tartalmazó vízfelületet írunk le táblázatos módon a - honlapunkról letölthető - jegesviz.txt állományban. Ebben egy N×N-es négyzet alakú táblázat van, amelynek celláiban a V karakter vizet és a J jeget jelentsen. A táblázat szélén lévő cellák vizet tartalmaznak.

A jegesviz.txt állomány első sorában egy egész szám van (3N100), amely a táblázat sorainak és oszlopainak számát jelenti. A következő N sor mindegyike N karaktert (V vagy J) tartalmaz.

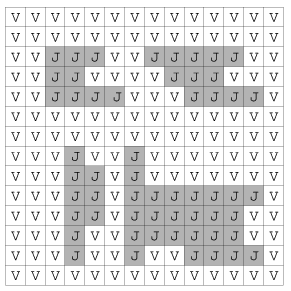
A jegesviz.txt állomány első néhány sora:

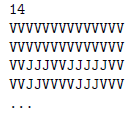
Készítsünk programot i310 néven, amely megoldja az alábbi feladatokat. Az egyes feladatok megoldása előtt jelenítsünk meg a képernyőn a feladat sorszámát tartalmazó szöveget (például: 2. feladat). Az ékezet nélküli kiírás is megengedett.

1. Olvassuk be és tároljuk a jegesviz.txt állomány adatait.

2. Írjuk a képernyőre a fájlban található táblázat alapján, hogy a vizsgált felület hány százalékát fedi jég. Az eredményt két tizedes jegy pontossággal adjuk meg.

3. Adjuk meg, hogy a táblázat melyik oldalához van legközelebb jég. Ha több megoldás is van, akkor elegendő egyet megadni. Például: Az alsó oldalhoz van legközelebb jég.

4. A táblázat J tartalmú cellái jégtáblát alkotnak. A jégtábla állhat egy vagy több J cellából. A több cellás jégtáblánál minden J cella 4 szomszédja közül legalább 1 szintén J-t tartalmaz. Írjuk a képernyőre a jégtáblák számát.

5. Határozzuk meg a legnagyobb jégtáblát alkotó J cellák számát, és az eredményt írjuk a képernyőre.

6. A jégtáblák időegységenként a szélükön olvadnak. A J-t tartalmazó cella V tartalmú lesz, ha négy oldalszomszédja közül legalább kettő V. Írjuk a képernyőre, hogy hány időegység után olvad el az összes jégtábla.

Beküldendő a program forráskódja (i310.pas, i310.cpp, ...) és rövid dokumentációja (i310.txt, i310.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

Példa bemenet: jegesviz.txt

(10 pont)

megoldás, statisztika

---

I. 311. Egy park frissen rendezett téglalap alakú területén járólaprakó géppel teszik le az egységnyi oldalhosszúságú négyzet alakú betonlapokat. A gép egy lépésben előre, hátra, illetve jobbra vagy balra egy egységnyit tud lépni. Minden lépésnél egy betonlapot letesz a földre. A járólapfektetés közben önmagát keresztezheti az út. A gép ebben az esetben egymásra rakja a lapokat. Az így keletkező felesleget később össze kell gyűjteni.

A gép munkájához előre meg kell adni az útvonalát a terület vízszintes és függőleges hosszegységekben mért koordináta-sorozatával egy állományban. Az állomány soronként tartalmazza a gép x és y koordinátáit (3N100). A gép egy feltöltéssel, egy programmal maximum 200 járólapot tud letenni és a terület bármely pontjából indulhat.

Táblázatkezelő program segítségével oldjuk meg a következő feladatokat. A megoldásban saját függvény vagy makró nem használható.

1. Töltsük be a tabulátorokkal tagolt, UTF-8 kódolású - honlapunkról letölthető - utterv.txt szövegfájlt a táblázatkezelőbe az A1-es cellától kezdődően. Munkánkat i311 néven mentsük el a táblázatkezelő alapértelmezett formátumában.

2. Sorok és oszlopok beszúrásával, majd a cellák feltöltésével hozzuk létre a minta szerinti fejlécet.

3. A járólaprakó gép útvonalát, a területre lerakott betonlapok helyét karakteres formában is megjelenítjük. Ehhez végezzünk el néhány beállítást. A megjelenítéshez használandó oszlopok szélességét és sorok magasságát állítsuk be úgy, hogy a cellák négyzet alakúak legyenek a képernyőn. A sor- és oszlopkoordinátákat félkövér betűstílussal jelenítsük meg.

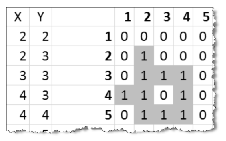
4. Másolható függvény segítségével a terület minden pontjában határozzuk meg, hogy a gép programjának végrehajtása után hány betonlap lesz azon a helyen. Segédszámításokat tetszőleges oszlopban végezhetünk, de ezeket ne rejtsük el.

5. Feltételes formázással emeljük ki a cellamintázat színezésével a gép útvonalát. A munkalapot nevezzük át Terkep nevűre.

6. A munkafüzetben hozzunk létre új munkalapot Elemzes néven. A további kérdésekre ezen a munkalapon válaszoljunk. Segédszámításokat itt is tetszőleges oszlopban végezhetünk, de ezeket se rejtsük el.

7. Számoljuk ki, hogy az egész terület hány százaléka járólap nélküli.

8. Mennyi az egymásra letett betonlapok maximális száma és hol van ez? Több azonos értékű pont esetén elég az egyik koordinátáit megadni.

9. Adjuk meg a terület négy széléhez legközelebbi betonlapok koordinátáit. Azonos távolságú járólapok esetén csak az egyikét.

10. Számoljuk meg, hogy hány darab járólapot kell elvinni ahhoz, hogy egymásra téve egy se maradjon.

11. Ha a felesleges járólapokat csak egyesével tudjuk elvinni a (0;0) koordinátájú, a területen kívül eső pontba, akkor mekkora utat kell összesen megtenni? A szállítás során csak felfelé és balra léphetünk.

Beküldendő a táblázatkezelő munkafüzet (i311.xls, i311.ods, ...), illetve egy rövid dokumentáció (i311.txt, i311.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.

Letölthető állomány: utterv.txt

(10 pont)

megoldás, statisztika

---

I. 312. Egyre több weboldalon látunk ilyen, vagy ehhez hasonló képet:

Ez az informatika érettségi emelt szintű szóbeli témaköreinek címkefelhője, pontosabban szövegfelhője. A wikipedia szerint ,,a címkefelhő egy weboldal tartalmára jellemző címkék vagy szövegbeli szavak olvasók általi használati gyakorisága vagy más fontos tulajdonsága szerinti vizuális ábrázolása. A címkék többnyire kulcsszavak, melyeket általában betűrendben sorolnak fel, és fontosságukat színük vagy betűméretük jelzi. E módon abc-helyük és fontosságuk alapján is meg lehet őket találni.''

Keressünk minél több, szövegfelhő készítésére alkalmas eszközt, programot. Válasszunk ki egyet közülük és segítségével végezzük el néhány szöveg összehasonlító vizsgálatát. Vessük össze a belőlük készült címkefelhők alapján

egy neves költő életművének két különböző évében született verseinek szövegét;

egy író két regényét;

két, azonos témájú tudományos művet.

Válasszunk egy másik eszközt és az egyik regényt vizsgáljuk meg ennek segítségével is.

Készítsünk prezentációt, amelyben az eredmények bemutatása mellett összefoglaljuk tapasztalatainkat, következtetéseinket.

Beküldendő a prezentáció (i312.ppt, i312.odp, ...) és a feladat vizsgálat dokumentálása (i312.pdf), amely tartalmazza a talált eszközök megnevezését és azok elérhetőségét.

(10 pont)

megoldás, statisztika

S-jelű feladatok A beküldési határidő 2013. február 11-én LEJÁRT.

---

S. 77. Egy robot útját kell megterveznünk egy akadálypályán úgy, hogy minél hamarabb érje el a célvonalat. A célvonal az x tengely, az akadályok pedig ezzel párhuzamos szakaszok, melyeken a robot nem képes áthaladni. (A szakaszokat ideálisnak tekintjük olyan értelemben, hogy az y tengely irányában 0 a kiterjedésük.) A robot csak a tengelyekkel párhuzamosan tud mozogni. Írjunk programot, amely az akadályok végpontjai és a robot kezdeti pozíciója alapján megadja, hogy milyen hosszú a legrövidebb út, amelyen a robot elérheti a célt.

Bemenet: A standard input első sorában az akadályok száma található (), a másodikban a robot kezdeti pozíciójának x és y koordinátája egy szóközzel elválasztva. A következő N sor leírja egy-egy akadály helyét három, szóközzel elválasztott számmal, melyek közül az első megadja az y koordinátáját, a következő kettő pedig a két végpontjának x koordinátáit. Mindegyik koordináta 1000000-nál kisebb pozitív egész szám. Az akadályok nem érintkeznek egymással, továbbá a hosszuk nem 0.

Kimenet: A standard output egyetlen sorába írjuk ki a legrövidebb út hosszát.

Példák:

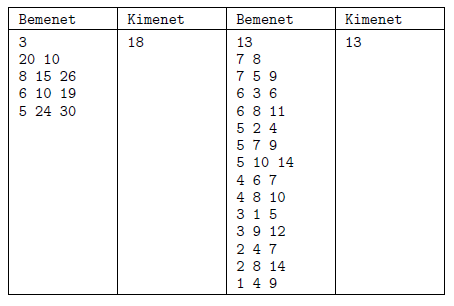
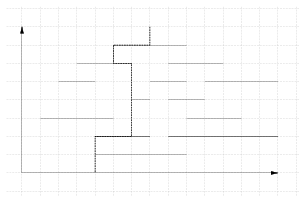
Értékelés: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 2 pontot ér. A programra akkor kapható meg a maximális 8 pont, ha bármilyen, a feltételeknek megfelelő tesztesetet képes megoldani 3 mp futásidőkorláton belül. A megoldásra részpontszám kapható, ha a program csak kisebb tesztesetekre tud lefutni időben, pl. ha a program csak olyan bemeneteket tud megoldani, amelyeknél a koordináták 0 és 100 közötti számok.

Beküldendő egy tömörített s77.zip állományban a program forráskódja (s77.pas, s77.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, a program rövid dokumentációja (s77.txt, s77.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrás mely fejlesztői környezetben fordítható.

Gyebnár Gábor ötlete nyomán

Mintabemenetek: Tesztek.zip

(10 pont)

megoldás, statisztika